Title Requirements
Write a program to build the binary list storage structure of the binary tree by using the first order recursive calendar (or input the first order and the middle order recursive traversal node access sequence), calculate and output the total number of nodes and the height of the binary tree, and then output the first order, the middle order, the second order and the hierarchical traversal node access sequence. The implementation of hierarchical traversal needs to use cyclic queue. Character type is recommended for binary tree node data type.
Data structure design
Use c + + template class to create queues. In each queue object, the elem pointer is used to create an array of length N, where n represents the capacity of the queue, front represents the head pointer, rear represents the tail pointer, and c represents the number of current elements in the queue.
The binary tree is built with structure, where data represents data domain, lchild represents left pointer, rchild represents right pointer, BiT represents pointer type variable of binary tree structure, BiTNode represents binary tree structure type variable.
Brief description of algorithm design
- First, traverse to build a binary tree: call the function recursively, read the characters continuously, build the left subtree and the right subtree in turn, when the '#' character is read, return NULL pointer, and finally return the root node pointer.
- A binary tree is established by traversing the node access sequence in the first and middle order
a. First, the root node is obtained from the sequence;
b. Then, from the position of the root node in the middle order sequence, we know that the node it visited before is its left subtree node, and the node it visited after is its right subtree node;
c. Recursively apply a and b.
Program code
#include <conio.h> #include <iostream> using namespace std; typedef char ElemTp; #define MAX 20 template <typename T> class Queue //Template class: queues { public: Queue(); //Default constructor Queue(int n); //Constructor, call the function createQueue(int n) to create a queue of length n ~Queue(); //Fictitious function int createQueue(int n); //Create a queue of length n int empty(); //Judge whether the queue is empty int full(); //Judge whether the queue is full int enQueue(T e); //Element e joins the team int dlQueue(T &e); //Element out of team, saved in e private: T *elem; //Create an array of length n int n; //Queue capacity int front; //Team leader pointer int rear; //End of line pointer int c; //Number of current elements in the queue }; typedef struct node { ElemTp data; //Data field struct node *lchild, //Left pointer *rchild; //Right pointer }*BiT,BiTNode; void visit(BiT e) //Access function { if (e->data != NULL) //Data field of output binary tree cout << e->data << " "; } void preorder(BiT bt) //First order traversal binary tree { if (bt) { visit(bt); //Access root node preorder(bt->lchild); //Recursive call traversing left subtree preorder(bt->rchild); //Recursive call traversing right subtree } } void midorder(BiT bt) //Middle order ergodic binary tree { if (bt) { midorder(bt->lchild); //Recursive call traversing left subtree visit(bt); //Access root node midorder(bt->rchild); //Recursive call traversing right subtree } } void lasorder(BiT bt) //Postorder ergodic binary tree { if (bt) { lasorder(bt->lchild); //Recursive call traversing left subtree lasorder(bt->rchild); //Recursive call traversing right subtree visit(bt); //Access root node } } void layertravel(BiT bt) //Hierarchical ergodic binary tree { if (bt == NULL) return; Queue<BiT> q(MAX); //Queue up q.enQueue(bt); //Root node joining the team while (!q.empty()) { q.dlQueue(bt); //Root out visit(bt); //Access root node if (bt->lchild) q.enQueue(bt->lchild); //Left subtree is not empty, access left subtree if (bt->rchild) q.enQueue(bt->rchild); //Right subtree is not empty, access right subtree } } BiT crtPreBT() //An algorithm of building binary tree by first order recursive traversal { BiT bt; char ch; ch = getchar(); if (ch == '#') //Read '×' and return NULL pointer return NULL; bt = new BiTNode(); //Building a new node of binary tree bt->data = ch; bt->lchild = crtPreBT(); //Recursively building left subtree bt->rchild = crtPreBT(); //Recursively building right subtree return bt; } BiT crtPreMidBT(char *pr, int &i, char *mi, int u, int v) //A binary tree algorithm for recursive traversal of node access sequences in preorder and middle order { BiT bt; int k; if (u > v) return NULL; bt = new BiTNode(); bt->data = pr[i++]; //pr[i] is the root node of the subtree for (k = u; k <= v; k++) //mi[u...v] is the ordered sequence in subtree { if (mi[k] == bt->data) //Find the position of the root node in the middle order sequence break; } bt->lchild = crtPreMidBT(pr, i, mi, u, k - 1); //Recursively building left subtree bt->rchild = crtPreMidBT(pr, i, mi, k + 1, v); //Recursively building right subtree return bt; } int height(BiT bt) //Calculating the height of a binary tree { int hl, hr; if (!bt) return 0; hl = height(bt->lchild); //Recursively calculating the height of the left subtree hr = height(bt->rchild); //Recursively calculating the height of right subtree return (hl > hr) ? (hl + 1) : (hr + 1); //Returns the height of the entire binary tree (the higher the height of the left and right subtrees plus one) } int nodeNum(BiT bt) //Calculating the sum points of binary tree { int nl, nr; if (!bt) return 0; nl = nodeNum(bt->lchild); //Recursively calculating the number of nodes in the left subtree nr = nodeNum(bt->rchild); //Recursively calculating the node number of right subtree return nl + nr + 1; //Returns the number of nodes of the entire binary tree (the sum of nodes of left and right subtrees plus one) } void choose(BiT &bt) //Choose how to build a binary tree { char num, pre[MAX], mid[MAX]; int i = 0, u = 0, v; cout << "Please choose how to build a binary tree: " << endl; cout << "1. First order traversal to build binary tree" << endl; cout << "2. Building binary tree by traversing the first order and the middle order" << endl; num = _getch(); switch (num) { case '1': //First order traversal to build binary tree { cout << "You chose the first way." << endl; cout << "Please enter the sequence of characters traversed first: " << endl; bt = crtPreBT(); } break; case '2': //Building binary tree by traversing the first order and the middle order { cout << "You chose the second way." << endl; cout << "Please enter the sequence of characters traversed first: " << endl; cin.getline(pre, MAX); cout << "Please enter the character sequence traversed by middle order: " << endl; cin.getline(mid, MAX); v = strlen(mid) - 1; bt = crtPreMidBT(pre, i, mid, u, v); } break; } } template<typename T> Queue<T>::Queue() { front = rear = -1; c = 0; } template<typename T> Queue<T>::Queue(int n) { createQueue(n); } template<typename T> Queue<T>::~Queue() { c = 0; front = rear = -1; delete[]elem; } template<typename T> int Queue<T>::createQueue(int n) { if (n <= 0) return 0; this->n = n; c = 0; front = rear = -1; elem = new T[n]; if (!elem) return 0; return 1; } template<typename T> int Queue<T>::empty() { return c == 0; } template<typename T> int Queue<T>::full() { return c == n; } template<typename T> int Queue<T>::enQueue(T e) { if (c == n) return 0; //Team full, team failure rear = (rear + 1) % n; elem[rear] = e; c++; return 1; //Team entry success return 1 } template<typename T> int Queue<T>::dlQueue(T & e) { if (c == 0) return 0; //Team empty, team failure front = (front + 1) % n; e = elem[front]; c--; return 1; //Team exit success return 1 } int main() { int h, num; BiT bt; choose(bt); h = height(bt); cout << "The height of a binary tree is: " << h << endl; num = nodeNum(bt); cout << "The sum points of binary trees are: " << num << endl; cout << "First order traversal node access order: " << endl; preorder(bt); cout << endl; cout << "Middle order traversal node access order: " << endl; midorder(bt); cout << endl; cout << "Post order traversal node access order: " << endl; lasorder(bt); cout << endl; cout << "Hierarchical traversal node access order: " << endl; layertravel(bt); cout << endl; return 0; }
Example
(1) Program input:
Sequence sequence: ABC × f###
Program output:
The height of a binary tree is: 5
The sum points of binary tree are: 7
a b c d e g f
Middle order ergodic: c b e g d f a
Postorder traversal: cgefdba
Hierarchical traversal: a b c d e f g
(2) Program input:
Preamble: ABCDEFG
Middle sequence: CBEDAFG
Program output:
The height of a binary tree is: 4
The sum points of binary tree are: 7
Preorder traversal: A B C D E F G
Middle order traversal: C B E D A F G
Postorder traversal: C E D B G F A
Hierarchical traversal: A B F C D G E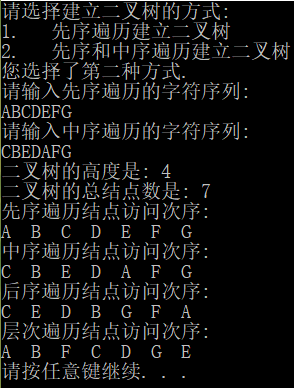
(3) Program input:
Sequence: abdf × C × e × g × H##
Program output:
The height of a binary tree is: 5
The sum points of binary tree are: 8
Preorder traversal: A B D F C E G H
Middle order traversal: F D B A C E G H
Postorder traversal: F D B H G E C A
Hierarchical traversal: A B C D E F G H
(4) Program input:
Preamble:#
Program output:
The height of a binary tree is: 0
The sum points of binary tree are: 0