1, Algorithm efficiency

What is an algorithm? Generally, people define an algorithm as a finite set of instructions, which specify an operation sequence to solve a specific task.

An algorithm should have the following characteristics

1. Have input
2. Have output
3. certainty
4. Poverty
5. feasibility

There is always a standard for the quality of the algorithm, which can be roughly divided into the following

• Correctness
• Readability
• efficiency
• Robustness
• Simplicity

In addition to efficiency, several others can see the results of running code. But how to evaluate the efficiency?
Because different codes have different operation time under different hardware conditions, we measure complexity, including time complexity and space complexity.

Complexity

Complexity of algorithm

When the algorithm is written into an executable program, it needs time resources and space (memory) resources. Therefore, the quality of an algorithm is generally measured from the two dimensions of time and space, namely time complexity and space complexity.

Time complexity mainly measures the running speed of an algorithm, while space complexity mainly measures the additional space required for the operation of an algorithm. In the early days of computer development, the storage capacity of computer was very small. So I care about the complexity of space. However, with the rapid development of computer industry, the storage capacity of computer has reached a high level. Therefore, we no longer need to pay special attention to the spatial complexity of an algorithm.

2, Time complexity

Concept of time complexity
The time spent by an algorithm is directly proportional to the execution times of the statements in it. The execution times of the basic operations in the algorithm is the time complexity of the algorithm.

That is, finding the mathematical expression between a basic statement and the problem scale N is to calculate the time complexity of the algorithm.

Let's start with a program

void Fun1()
{
	int count = 0;//Program steps - 1
	for (int i = 0; i < N ; ++ i)   // 1
	{
		++count;           // N
	}
}

We can calculate the specific program steps N+2

void Fun2()
{
	int count = 0;
	for (int i = 0; i < N ; ++ i)
	{
		for (int j = 0; j < N ; ++ j)
		{
			++count;
		}
	}
}

Program steps 2*N2+2

In fact, when we calculate the time complexity, we do not have to calculate the exact execution times, but only the approximate execution times. Here, we use the asymptotic representation of large O.

Asymptotic representation of large O

Big O notation: a mathematical symbol used to describe the asymptotic behavior of a function.
Derivation of large O-order method:

• Replace all addition constants in the run time with constant 1.
• In the modified run times function, only the highest order term is retained.
• If the highest order term exists and is not constant, the coefficient associated with the term is removed. The result is large O-order.

Only the items that have the greatest impact on the results are retained. When the variables continue to increase, the impact of other items on the results is ignored.

After using the progressive representation of large O
The time complexity of Func1 is: O(N)
The time complexity of Func1 is O(N2)
The number of program steps is constant, i.e. O(1)

Worst case: maximum number of runs of any input scale (upper bound)
Average case: expected number of runs of any input scale
Best case: minimum number of runs of any input scale (lower bound)

Common time complexity calculation examples

#include<stdio.h>
void Func1(int N)
{
	int count = 0;
	for (int k = 0; k < 2 * N; ++k)
	{
		++count;//2*N
	}
	int M = 10;
	while (M--)
	{
		++count;//M=10, constant times
	}
	printf("%d\n", count);
}

Therefore, the time complexity of the function is O(N)

void Func2(int N, int M)
{
	int count = 0;
	for (int k = 0; k < M; ++k)
	{
		++count;//M times
	}
	for (int k = 0; k < N; ++k)
	{
		++count;//N times
	}
	printf("%d\n", count);
}

In this example, N and M are not constants, so the number of core steps is N+M and the time complexity is O(N+M)

void Func3(int N)
{
	int count = 0;
	for (int k = 0; k < 100; ++k)
	{
		++count;//100 times - constant times
	}
	printf("%d\n", count);
}

As long as the number of core code steps is constant, the number of times is O(1)

int Func4(int arr[], int n, int x)
{
	//Worst - n times
	//Best - 1 time
	//Average - (n+1) / 2
	for (int i = 0; i < n; ++i)
	{
		if (arr[i] == x)
		{
			return i;  
		}
			
	}
	//Search failed, return - 1
	return -1;	
}

We generally care about the worst case of the program, that is, O(N)

1. Calculating the time complexity of bubble sorting

void BubbleSort(int* a, int n)
{
	assert(a);
	for (size_t end = n; end > 0; --end)
	{
		int exchange = 0;
		for (size_t i = 1; i < end; ++i)
		{
			if (a[i - 1] > a[i])
			{
				Swap(&a[i - 1], &a[i]);
				exchange = 1;
			}
		}
		if (exchange == 0)
			break;
	}
}

In the face of this can not be seen directly, we first look for the core code sentence, that is, the judgment sentence in the double loop. Then let's look at its execution steps
In the best case, it is ordered without exchange, and the time complexity is - O(N)
In the worst case, it is exchanged every time. The number of executions: 1 + 2 + 3 + ···· + n = (n+1)*n/2
Time complexity - O(N2)

1. Binary search

int BinarySearch(int* a, int n, int x)
{
	int begin = 0;
	int end = n - 1;
	while (begin < end)
	{
		int mid = begin + ((end - begin) >> 1);
		if (a[mid] < x)
			begin = mid + 1;
		else if (a[mid] > x)
			end = mid;
		else
			return mid;
	}
	return -1;
}

For each comparison, the range is halved, in the best case O(1).
In the worst case, if the array is searched x times and the length is N, then there are N / 2 / 2 ·· / 2 = 1 and x 2, that is, 2x = N = > x = log2 (N) - (logarithm of N with 2 as the base) can also be abbreviated as logN, so the time complexity is O(logN)

1. Recursive factorial calculation

long long Fac(size_t N)
{
	if(0 == N)
		return 1;
	return Fac(N-1)*N;
}

It is easy to know that the function recurses N times, so the time complexity is O(N)

1. Fibonacci sequence

long long Fib(size_t N)
{
	if(N < 3)
		return 1;
	return Fib(N-1) + Fib(N-2);
}

This is complicated. Let's draw a picture to explain

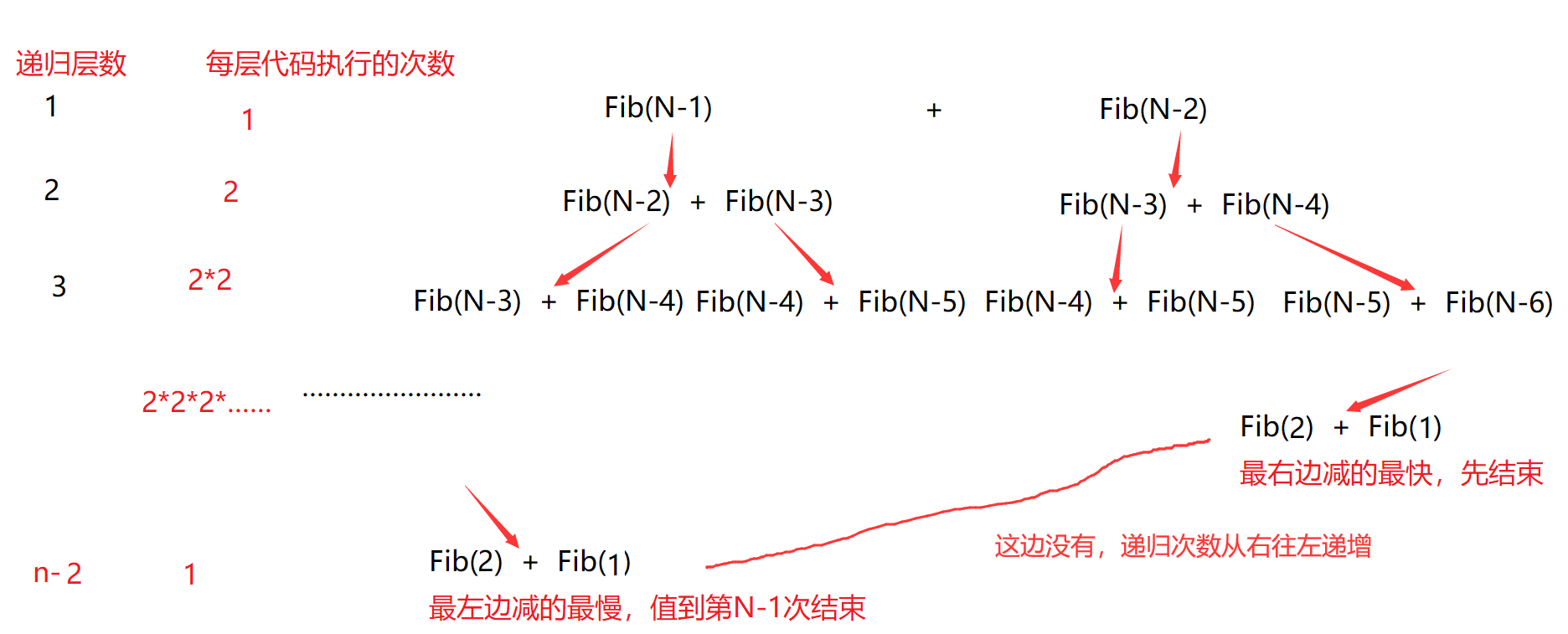
Because the time complexity represented by large O is calculated, it is OK to calculate an approximate.
Let's assume that the total recursive digits X that start missing later are added first, that is, an equal ratio sequence, that is, the sum of the equal ratio sequence in front of 1 + 2 + 22 + ····· + 2n-2-X, the highest order is 2n-2, and the time complexity is in place O(2n).

3, Spatial complexity

Space complexity is also a mathematical expression, which is a measure of the temporary storage space occupied by an algorithm during operation.
Spatial complexity is not how many bytes the program occupies, because it doesn't make much sense, so spatial complexity is the number of variables. The calculation rules of spatial complexity are basically similar to practical complexity, and the large O progressive representation is also used.

Note: the stack space (storage parameters, local variables, some register information, etc.) required by the function runtime has been determined during compilation, so the space complexity is mainly determined by the additional space explicitly applied by the function at runtime.

Let's look at some examples

void Func4(int N)
{
	int count = 0;
	for (int k = 0; k < 100; ++k)
	{
		++count;//100 times - constant times
	}
	printf("%d\n", count);
}

It can be seen that 1 (constant) additional space is used, so the space complexity is O(1)

1. Fibonacci sequence

// Returns the first n items of the Fibonacci sequence
long long* Fibonacci(size_t n)
{
	if(n==0)
		return NULL;
	long long * fibArray = (long long *)malloc((n+1) * sizeof(long long));
	fibArray[0] = 0;
	fibArray[1] = 1;
	for (int i = 2; i <= n ; ++i)
	{
		fibArray[i] = fibArray[i - 1] + fibArray [i - 2];
	}
	return fibArray;
}

The program malloc (dynamic development) has n+1 long long space, so the space complexity is O(N)

1. Recursive factorial calculation

long long Fac(size_t N)
{
	if(N == 0)
		return 1;
	return Fac(N-1)*N;
}

Recursive calls are made n times, and N stack frames (memory occupied by the function (on the stack)) are opened up. Each stack frame uses a constant space. The space complexity is O(N)

4, Common complexity comparison

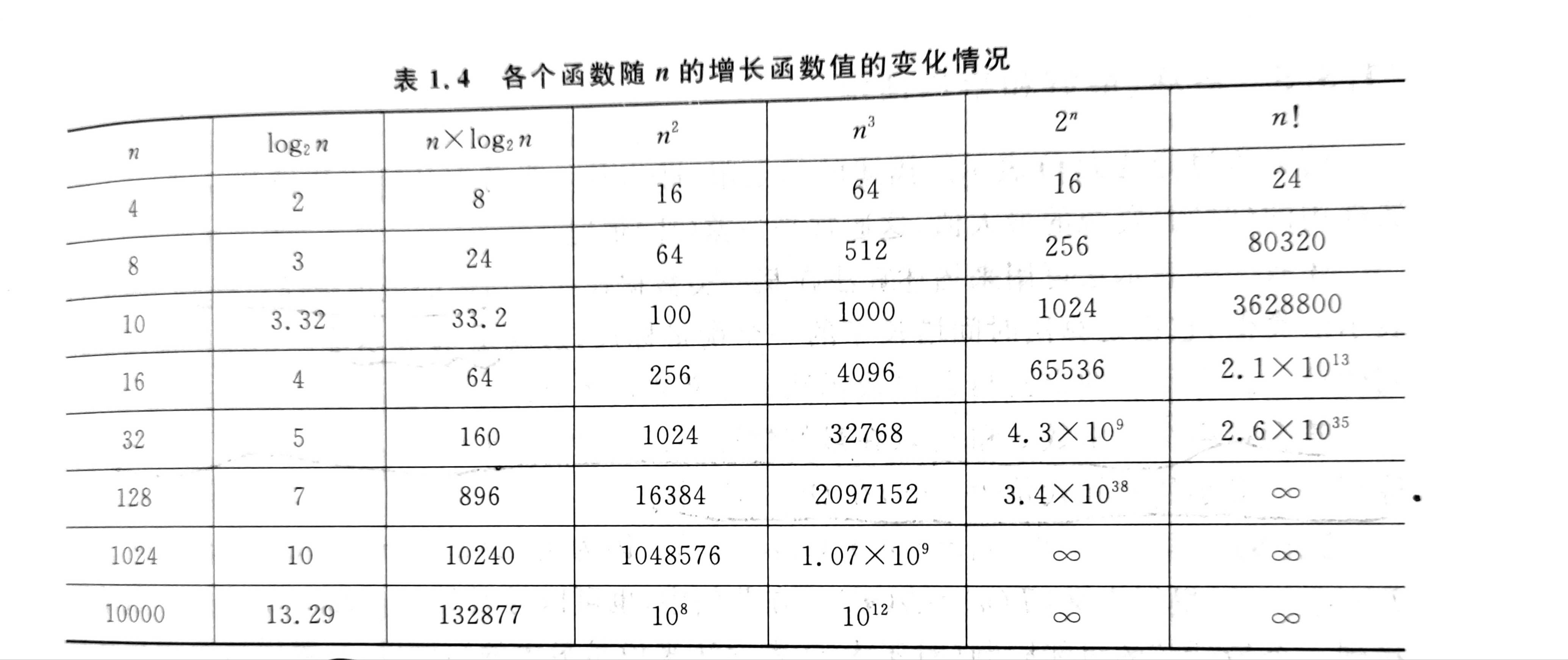
Generally speaking, the time complexity should be kept at or below NlogN. When the time complexity is N2, it can generally be converted to NlogN, and the speed is greatly improved.