Today we will summarize the sorting algorithms in the data structure.

Data structure Sorting Algorithm part1:


Direct insertion sort:

Thought: When inserting the I (i >= 1) element, the preceding array[0],array[1],... array[i-1] has been arranged
In this case, the sequence code of array[i] and array[i-1],array[i-2],... Compare the ranking order to find the insertion
The position inserts array[i] and the elements in the original position move backwards.


Simply put: end refers to the last element of the array that has been arranged. End finds the insertion position (set a temp, temp is the next element of the array that has been sorted). Temp is compared with end. If temp < array[end], array[end] is given to array[end+1], and temp is given to array[end].
 
Time complexity: O (N*N)
Spatial complexity: O (1)
Stability: If you encounter an element that is equal to the insertion element, the insertion element puts the element you want to insert behind the same element. Therefore, the order of the equal elements has not changed. The order from the original disordered sequence is the order after the order, so the insertion order is stable.

Code implementation:

void Insert_Sort(int array[],int size)
{
	// 2, 5, 4, 9, 3, 6, 8, 7, 1, 0
	for (int idx = 0; idx < size-1; ++idx)
	{
		int temp = array[idx+1];
		int end = idx;
		while (end>=0 && array[end]>temp)
		{
			array[end+1] = array[end];
			end--;
		}	
		array[end+1] = temp;
	}
}

Dichotomous lookup direct insertion sort:

Idea: Add the idea of dichotomy search on the basis of insertion sort to reduce the number of searches

Time complexity: O(log(n))
Spatial complexity: O(1)
Stability: Stable (with insertion lookup)
Code implementation:

//Binary search insertion sort
void Insert_Sort_P(int array[], int size)
{
	//Here idx starts from scratch to get closer to array subscripts
	for (int idx = 0; idx < size - 1; ++idx)
	{	
		int temp = array[idx + 1];
		int end = idx;
		int left = 0;
		int right = end;
		
		//Binary lookup to find intervals to insert
		while(left<=right)
		{
			int mid = left + ((right - left) >> 1);
			if (array[mid] > temp)
			{
				right = mid - 1;
			}
			//Here's the same insertion after that if it's equal.
			else
			{
				left = mid + 1;
			}
		}


		//The reason for this is that right-1 may end up being negative.
		while (end>=0&&end >= left)
		{
			array[end + 1] = array[end];
			end--;
		}
		//If the above while is not executed, then temp is still the value of end+1, which is equivalent to not doing it.
		array[end + 1] = temp;
	}
}

Hill Sort:
Idea: First, the whole sequence of records to be sorted is divided into several subsequences for direct insertion and sorting. Then, when the records in the whole sequence are "basically ordered", the whole record is directly inserted and sorted in turn.
 
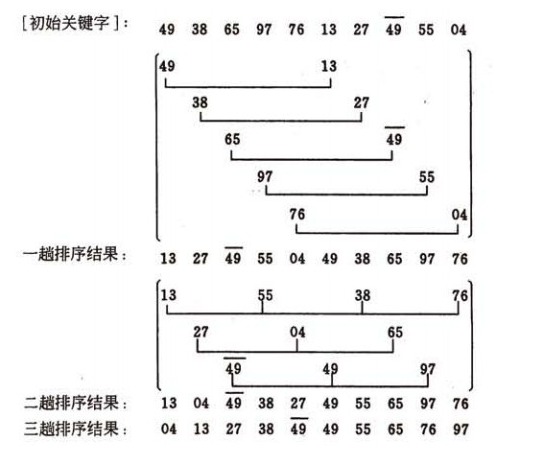
Time complexity: O (N ^ 1.25) - - O (1.6N ^ 1.25)
Spatial complexity: O(1)
Stability: instability
Code implementation:

//Shell Sort
void Shell_Sort(int array[],int size)
{
	int gap = size;
	//This must be >= 1 because the last possible interval is one row.
	while (gap >= 1)
	{
	gap = gap / 3 + 1;


		for (int idx = gap; idx < size; ++idx)
		{
			//Here temp is the value of gap subscript
			int temp = array[idx];
			int end = idx - gap;
			while (end >= 0 && array[end]>temp)
			{
				array[end + gap] = array[end];
				end -= gap;
			}
			array[end+gap] = temp;
		}
		gap--;
	}
}

Selection Sort:

Thought: Every trip (e.g. the first trip, i=0,1,... (n-2) Select the key among the subsequent n-i sets of data elements to be sorted
The data element with the smallest code is the first element in the sequence of ordered elements. When the n-2 rounds are finished, there is only one element left in the set of elements to be sorted, and the sorting ends.
 
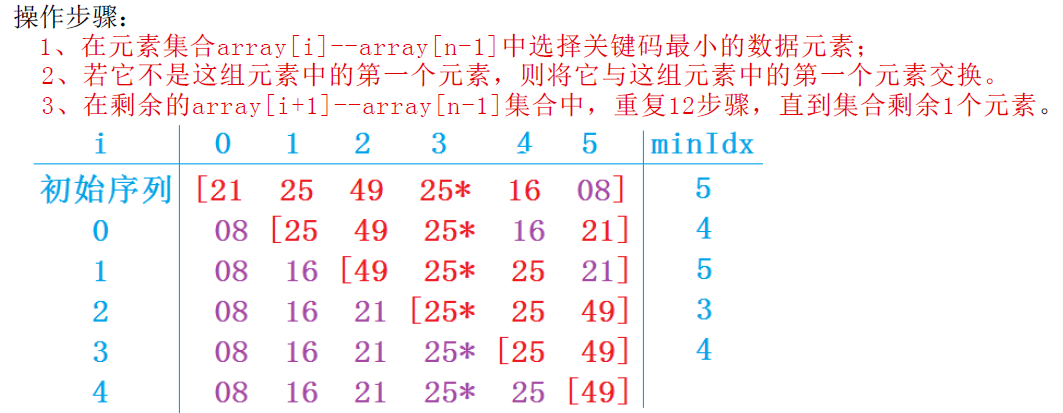
Time complexity: O(N*N)
Spatial complexity: O(1)
Stability: instability
Code implementation:

//Selection sort
void Select_Sort(int array[], int size)
{
	int min = 0;
	//Several trips can be arranged.
	for (int idx = 0; idx < size; ++idx)
	{
		min = idx;
		for (int index = idx + 1; index < size; ++index)
		{
			if (array[min] > array[index])
				min = index;
		}


		if (min != idx)
		{
			std::swap(array[min], array[idx]);
		}
	}
}

Optimizing the selection order:
Idea: Choose the largest and the smallest one at a time. The array is indented from both sides and decreases. Put the big one behind and the small one ahead. At this time, only half the number of times, you can sort a group of numbers.
Code implementation:

//Selective Sorting Optimization
void Select_Sort_Cool(int array[],int size)
{
	int min = 0;
	int max = 0;
	int left;
	int right;
	for (left = 0, right = size - 1; left<=right; left++, right--)
	{
		min = left;
		max = right;
		for (int idx = left; idx <= right; ++idx)
		{
			if (array[min] > array[idx])
				min = idx;


			if (array[max] < array[idx])
				max = idx;
		}


		if (min != left)
		{
			std::swap(array[min], array[left]);
		}
		if (max != right)
		{
			std::swap(array[max], array[right]);
		}
	}
}

Heap sort:

Idea: Sort the data by using the size heap. Build heap sorting. After each sorting, the array is subtracted by one, and the elements that have been sorted are excluded.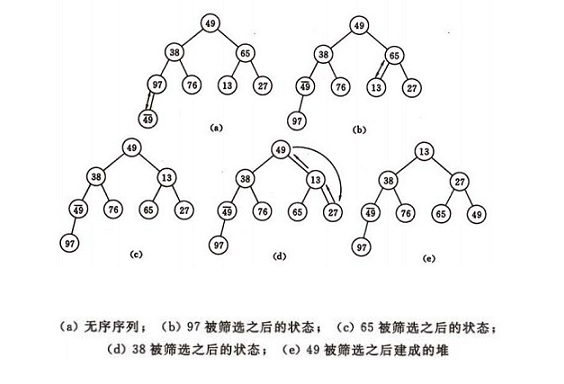
 
Time complexity: O (NlogN)
Spatial complexity: O (1)
Stability: instability
Code implementation:

//Build pile//root from top to bottom
void adjust_Down(int array[],int root, int size)
{
	int child = root * 2 + 1;
	int parent = root;


	while (child < size)
	{
		if (child+1 < size && array[child] < array[child+1])
		{
			child = child + 1;
		}
		if (array[parent] < array[child])
		{
			std::swap(array[parent],array[child]);
			parent = child;
			child = child * 2 + 1;
		}
		else
			break;
	}
}
//Heap sort
void Heap_Sort(int array[],int size)
{
	for (int idx = (size - 2) / 2; idx >= 0;--idx)
	{
		adjust_Down(array, idx, size);
	}
	int index = size - 1;
	while (index>0)
	{
		std::swap(array[0], array[index]);
		adjust_Down(array, 0, index);
		index--;
	}
}