Mind mapping

Linear table

• Definition

    It is a finite sequence consisting of n(n < 0) data elements (nodes) a1,a2....an. Among them, the number of data elements n is the length of the table. When n is zero, it is called an empty table.
  

• Logical Structural Characteristics

  • There is only one a1 called the starting element, which has no direct forward trend, and there is only one direct successor a2.
  • There is and only one end element an, without direct succession, and there is and only one direct forward trend an-1.
  • The other element nodes ai (2 < i < n-1) have only one direct forward ai-1 and one direct successor ai+1.

• Basic operation

  • InitList (L): Construct an empty linear table L, that is, table initialization, empty table
  • ListLength (L): Find the number of nodes in a linear table L, that is, the length of the table.
  • GetNode (L, i): Take the first node in the linear table L, where 1 < I < ListLength(L)
  • LocateNode (L, x): Find a node with a value of X in L and return the location of that node in L. If there are multiple nodes in L whose values are the same as x, the location of the first node is returned; if there are no nodes in L whose values are x, the value of 0 is returned.
  • InsertList (L, x, i): Insert a new node with a value of X at the first position of the linear table L. After insertion, the length of the table L is increased by 1.
  • DeleteList (L, i): Delete the first node of the linear table L and reduce the length of the table L by 1 after deletion.

• Example:

    [Example] Assuming that two linear tables LA and LB represent two A and B respectively, a new set A=A B is required.
    
    Idea: Expand the linear table LA and insert elements that do not appear in LA in LB into LA. As long as each element is extracted from the linear table LB in turn, it is searched in the linear LA by value and inserted if it is not found.
  

  void union(Linear_List LA,Linear_List LB){
      n=ListLength(LA); //Finding the Table Length of LA
      for(i=1;i<=ListLength(LB);i++){ 
          x=GetNode(LB,i); //Give x the first element in LB
          if(LocateNode(LA,x)==0) //Determine whether there is x in LA
              InsertList(LA,++n,x);
      }
  }
  

  Sequential List

• Definition

    The sequential storage of linear tables refers to storing the data elements of linear tables in logical order into a set of memory cells with continuous addresses. The linear tables stored in this way are called sequential tables.
  

  # The size of define ListSize 100//table space should be defined according to actual needs, assuming that it is 100
  typedef int DataType; //The type of DataType can depend on the actual situation, which is assumed to be int.
  typedef struct{
      DataType data[ListSize]; //Array data is used to store table nodes
      int length; //The current table length of a linear table (the number of elements actually stored)
  }SeqList
  

• Storage location

    LOC(ai)=LOC(a1)+(i-1)*d; 
  
    d: Each element needs to be occupied d A storage unit
    LOC(a1):Represented as the first element of a linear table a1 Storage location is usually called base address.
  

• Basic operation

  • insert

      The insertion element of linear table refers to the insertion of a new element x between the i-1 element and the i-1 element of the linear table, which makes the linear table with length n.
    

  void InsertList(SeqList *L,iny i,DataType x){
      int j;
      if(i<1 || i>L->Length+1){
          printf("position error");
          return;
      }
      if(L->length>=ListSize){
          printf("overflow");
          return;
      }
      for(j=l->Length-1;j>=i-1;j--){
          L->data[j+1]=L->data[j]; //Move back one by one from the last element
          L->data[i-1]=x; //Insert a new element x
          L->length++; //Actual table length plus 1
      }
  }
  

  • delete

      The deletion operation of linear tables refers to the deletion of the first i (1 < i < n) element in the table, so that the linear table with length n can be changed into a linear table with length n-1.
    

  DataType DeleteList(SeqList *L,int i){
      int jl
      DataType x;
      if(i<1 || i>L->Length){
          printf("position error");
          return;
      }
      x=L->data[i];
      for (j=i;j<=L->Length;j++){
          L->data[j-1]=L->data[j]; //Element move forward
          L->length--; //Actual table length minus 1
          return x; //Returns deleted elements
      }
      
  }
  

  Linked List

• Definition

    The storage space of linear dislike data elements in chain storage structure may be continuous or discontinuous, so the nodes of chain list can not be stored randomly.
  

  Single Linked List (Linear Linked List)

When using chain storage structure to represent each data element ai, besides storing the information of AI itself, a pointer indicating the storage location of its successor element ai+1 is also needed. The storage image of the two component elements AI is usually called a node. Since each node of this linked list contains only one pointer field, it is called a single linked list.

• Basic operation

  • Establishing a single linked list

    • Head insertion
      Head-insertion means to start from an empty table, read data repeatedly, generate new nodes, store the read data into the data field of the new nodes, and then insert the new nodes into the header of the current linked list until the end flag is read.
      

    LinkList CreateList(){
        LinkList head;
        ListNode *p;
        char ch;
        head=null; //Vacant single linked list
        ch=getchar(); //Read in the first character
        while(ch!='\n'){ //Loop when reading in a character is not an end sign
            p=(ListNode *)malloc(sizeof(ListNode)); //Apply for a new node
            p->data=ch; //Data Domain Assignment
            p->next=head; //Pointer field assignment
            head=p; //Header Pointer Executes New Node
            ch=getchar(); //Read in the next character
        }
        return head; //Header pointer to return list
    }
    

    • Tail insertion method (without leading node)

      Inserting a new node at the end of a single linked list requires adding a tail pointer rear so that it always points to the end of the list.
      

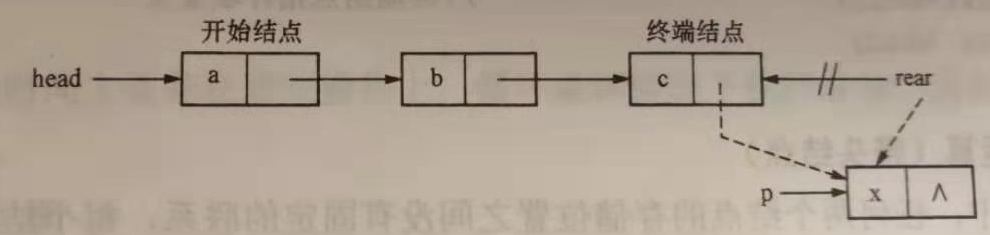
    LinkList CreateList(){
        LinkList head,rear;
        ListNode *p;
        char ch;
        head=NULL;rear=NULL; //Empty table
        ch=getchar(); //Read in the first character
        while(ch!='\n'){ //Loop when reading in character 2 is not an end marker
            p=(ListNode *)malloc(sizeof(ListNode)); //Apply for a new node
            p->data=ch; //Data Domain Assignment
            if(head=NULL) head=p; //New node * p inserts empty table
            else rear->nexr=p; //The new node * p is inserted after the table of the non-empty table is the node * rear
            rear=p; //The end pointer points to the new end of the table
            ch=getchar();//Read in the next character
        }
        if(rear!=NULL) rear-next=NULL;  //Null pointer field of terminal node
        return head;
    }
    

    • Tail insertion method (leading node)

      In order to simplify the algorithm and facilitate operation, a node can be added before the beginning node of the list, which is called the head node.

      

    LinkList CreateList(){
        LinkList head=(ListNode *)malloc(sizeof(ListNode)); //Application Header Node
        ListNode *p,*r;
        DataType ch;
        r=head;
        while((ch=getchar())!='\n'){
            p=(ListNode *)malloc(sizeof(ListNode));
            p->data=ch; //After the new node is connected to the endpoint
            r->next=p; //The tail pointer points to the new node
            r=p; //Null pointer field of terminal node
        }
        r->next=NULL;
        return head;
    }
    

  • Finding operations (leading nodes)

    • Find by Node Number

    ListNode * GetNode(LinkList head,int i){
    //head is a single linked list with many header pointers for leading nodes, and i is the serial number of the nodes to be looked up.
    //If the lookup is successful, the storage address of the lookup node is returned, otherwise NULL is returned.
        ListnNode *p;int j;
        p=head->next; //Make p point to the first node
        j=1;
        while(p!=NULL&&j<i){ //Look back clockwise until p points to the first node or p is empty
            p=p->next;
            ++j;
        }
        if(j==i){
            return p;
        }else {
            return NULL;
        }
    }
    

    • Find by Node Value

    ListNode * LocateNode(LinkList head,DataType k){
        ListNode *p=head->next;
        while(p&&p->data!=k){ //Loop until p equals NULL or p - > Data equals k
            p=p->next;
        }
        return p;
    }
    

  • Insertion Operations (Leading Nodes)

    Let p point to the location of ai-1 first, then generate a new node * s whose data field value is x, and then insert it.

    

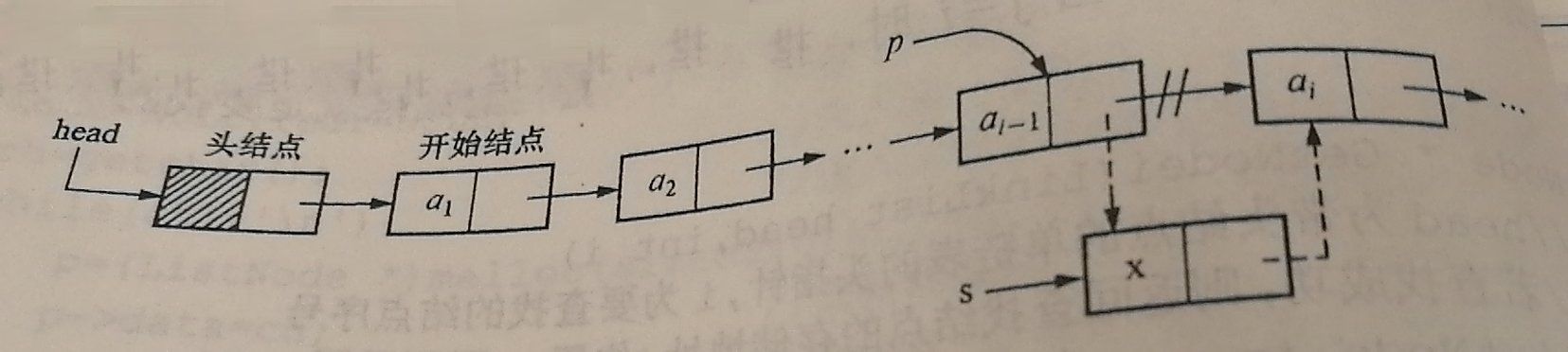
  void InsertList(LinkList head,int i,DataType x){
      ListNode *p,*s;
      int j;
      p=head;
      j=0;
      while(p!=NULL&&j<i-1){
          p=p->next;
          ++j;
      }
      if(p==NULL){
          printf("ERROR\n");
          return;
      }else{
          s=(ListNode *)malloc(sizeof(ListNode)); //Apply for a new node
          s->data=x;
          s->next=p->next;
          p->next=s;
      }
  }
  

  • Delete operations (leading nodes)

    Since the storage address of the first node is stored in the pointer field next of the i-1 node, it is necessary to make P point to the I-1 node first, then make p - > next point to the i+1 node, and then release the i-1 node.

    

  DataType DeleteList (LinkList head,int i){
      ListNode *p,*s;
      DataType x;
      int j;
      p=head;
      j=0;
      while(p!=NULL&&j<i-1){ //Make p point to node i-1
          p=p->next;
          ++j;
      }
      if(p==NULL){
          printf("Wrong location\n");
          exit(0);
      }else{
          s=p->next; //s points to node i
          p->next=s->next; //Make p - > next point to i+1 node
          x=s->data;//Save the value of the deleted node
          free(s); //Delete node i
          return x;
      }
  }
  

  Cyclic Link List (Linear Link List)

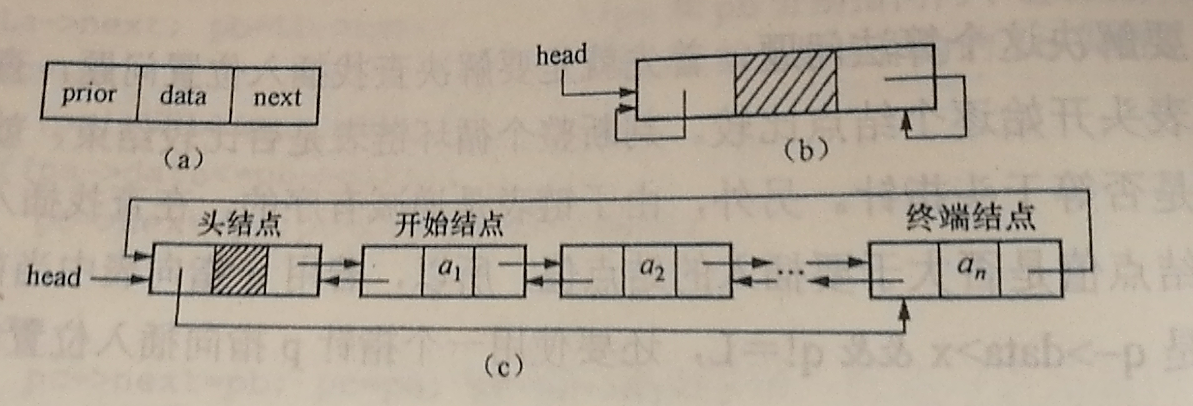
    The pointer field of the last node (terminal node) in the single list is not empty, but points to the head node of the list, which makes the whole list form a loop.
  

  

  Bidirectional Link List (Linear Link List)

  If we want to quickly determine the direct forward trend of a node from the list, we only need to add a pointer field prior to the node type of the single-linked list to point to its direct forward trend. In this way, there are two chains in different directions in the linked list, so it is called two-way linked list.

  

compare