1. What is red black tree?
The red black tree is first a self balanced binary search tree. The height difference between the left and right subtrees may be greater than 1, so the red black tree is not strictly balanced binary tree (AVL), but the cost of balancing it is low, and its average statistical performance is better than AVL.
It has the following characteristics:
- Node color is either red or black
- Root node black
- Leaf node black (empty node)
- Red nodes cannot be continuous
- Any path from node to empty node has the same number of black nodes
2. Principle
2.1 left and right rotation
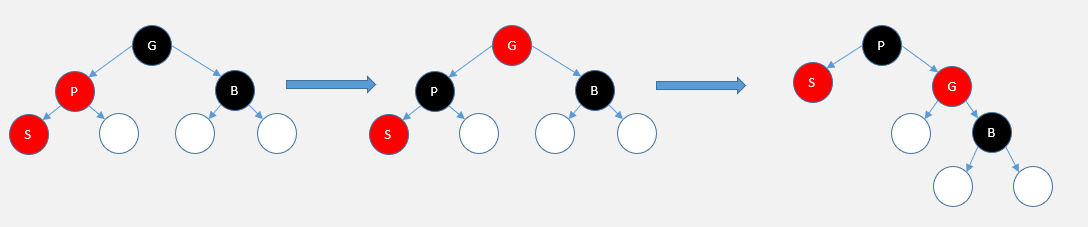
As shown in the figure below, set the imbalance node as S, the parent node as P, the parent node as G, and the P brother node as B.
1) If the characteristic (4) is satisfied, black P; At this time, the black length on the left is increased by one.
2) If the characteristic (5) is satisfied, G is painted red; At this time, the black length on the right is reduced by one.
3) If the characteristic (5) is satisfied, rotate to the right with P as the center;; At this time, the red and black trees are in balance.
2.1. Add node
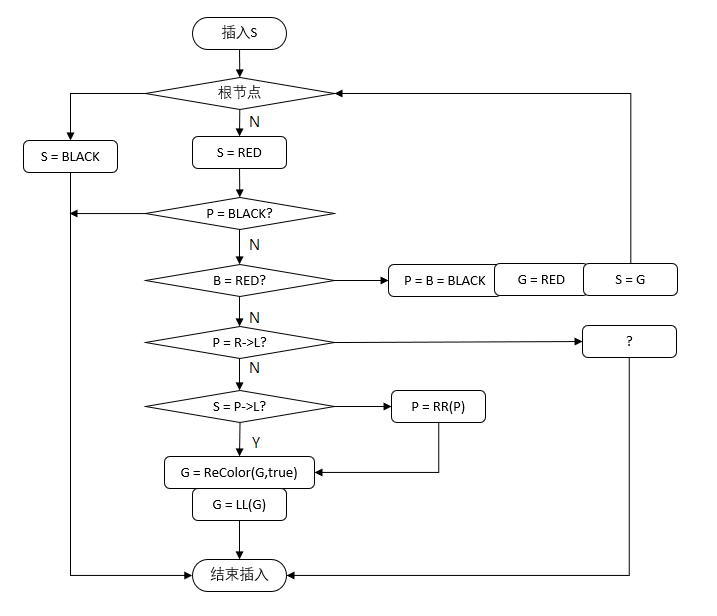
Firstly, according to the principle of binary tree, insert new nodes.
Set the imbalance node as S, the parent node as P, the grandfather node as G, and the brother node of P as B.
The basic process of inserting is as follows:
1) Determine whether the root node
2) Judge parent node color
3) Determine which branch of the parent node belongs to the parent node
4) Determine which branch of the parent node the unbalanced node belongs to
2.2. Delete node
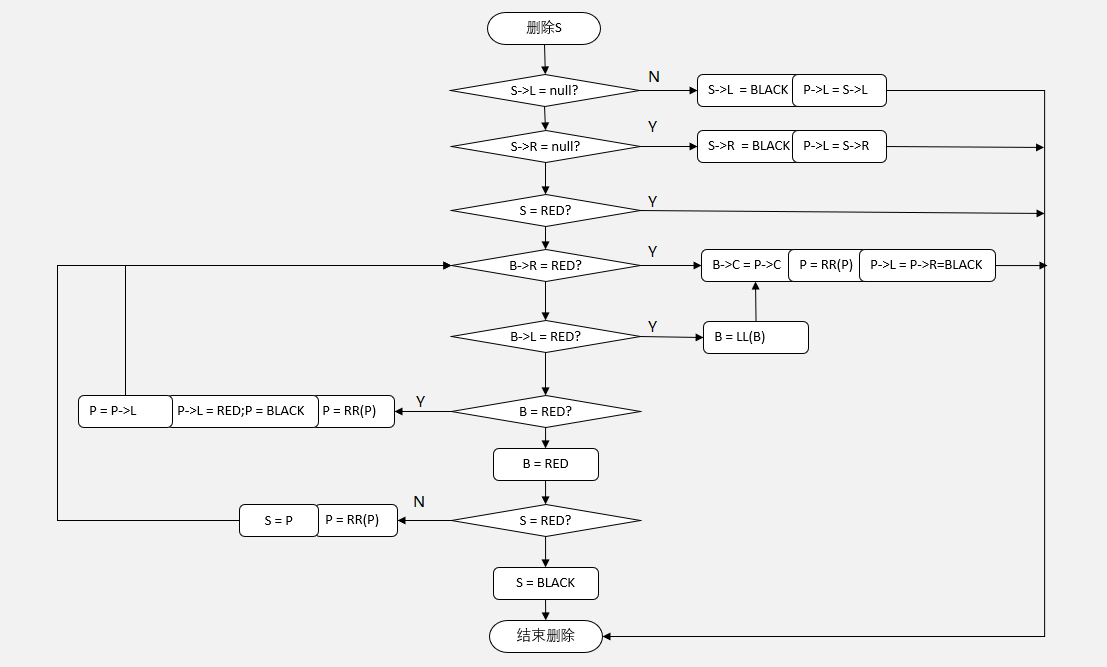
Firstly, according to the principle of binary tree, delete the specified node S.
Set the imbalance node as S (S = P - > L), the parent node as P, and the brother node as B.
The basic process of inserting is as follows:
1) Determine whether there is a left node
2) Determine whether there is a right node
3) Judge node color
4) Judge the right node color of brother node
5) Judge the left node color of sibling nodes
6) Judge parent node color
3. Examples
Simple implementation
enum RBColor { RED, BLACK };
template <class K, class V>
class RBTree {
private:
class RBNode {
private:
friend class RBTree;
K key;
V val;
RBColor color;
RBNode *l;
RBNode *r;
RBNode *p;
public:
RBNode(RBNode *parent, K key, V data) : p(parent), key(key), val(data) {
this->l = this->r = nullptr;
if (this->p == nullptr)
this->color = BLACK; // 2)
else
this->color = RED; // 5)
}
~RBNode() { ; }
};
void DelNode(RBNode *node) {
if (node != nullptr) {
DelNode(node->l);
DelNode(node->r);
delete node;
}
}
bool isRed(RBNode *node) {
if (node == nullptr) return false;
if (node->color == RED)
return true;
else
return false;
}
RBNode *ReColor(RBNode *node) {
if (node != root) node->color = RED;
node->l->color = node->r->color = BLACK;
return node;
}
RBNode *ReColor(RBNode *node, bool left) {
node->color = RED;
if (left)
node->l->color = BLACK;
else
node->r->color = BLACK;
return node;
}
RBNode *LL(RBNode *node) {
RBNode *_new = node->l;
// Update child node information
node->l = _new->r;
if (node->l != nullptr) node->l->p = node;
_new->r = node;
// Update parent node information
_new->p = node->p;
node->p = _new;
return _new;
}
RBNode *RR(RBNode *node) {
RBNode *_new = node->r;
node->r = _new->l;
if (node->r != nullptr) node->r->p = node;
_new->l = node;
_new->p = node->p;
node->p = _new;
return _new;
}
/*
* There are three situations for red black tree insertion: (1,2 no special treatment is required)
* 1) Insert root node
* 2) Parent node black
* 3) Parent / uncle red, grandfather black
* 3)After recursion, the following occurs:
* 3-1) Parent node (black, same as 2)
* 3-2) Parent node / uncle red, grandfather node black, the same as 3)
* 3-3) Parent node red, uncle node / grandfather node black
*/
RBNode *add(RBNode *parent, RBNode *node, K key, V data, int &weight) {
if (node == nullptr) {
weight = 3;
return new RBNode(parent, key, data);
}
if (key < node->key) {
node->l = add(node, node->l, key, data, weight);
if (weight) {
weight = (weight == 3) ? -3 : weight;
weight = weight - 1;
}
} else if (key > node->key) {
node->r = add(node, node->r, key, data, weight);
weight = (weight == 0) ? weight : weight + 1;
}
return rebalance(node, weight);
}
RBNode *get(RBNode *node, K key) {
if (node == nullptr) return nullptr;
if (node->key == key)
return node;
else if (key < node->key)
return get(node->l, key);
else
return get(node->r, key);
}
RBNode *Max(RBNode *node) {
while (node->r != nullptr) {
node = node->r;
}
return node;
}
RBNode *rebalance(RBNode *node, int &weight) {
switch (weight) {
case -5: // At this time, the red length of the left subtree is increased by 1
case 3:
if ((node->l->l != nullptr && isRed(node->l->l)) ||
(node->l->r != nullptr && isRed(node->l->r))) {
if (isRed(node->l)) {
if (isRed(node->r)) // Insertion scenario (3-2)
{
node = ReColor(node);
weight = 3;
break;
} else { // Insertion scenario (3-3)
if (weight == 3) node->l = RR(node->l); // Convert to ll case
node = ReColor(node, true); // Resolution feature 4)
node = LL(node); // Resolution feature 5)
}
}
}
weight = 0;
break;
case 5: // At this time, the red length of the right subtree is increased by 1
case -3:
if ((node->r->r != nullptr && isRed(node->r->r)) ||
(node->r->l != nullptr && isRed(node->r->l))) {
if (isRed(node->r)) {
if (isRed(node->l)) // Scenario 3-2)
{
node = ReColor(node);
weight = 3;
break;
} else { // Scenario 3-3)
if (weight == -3) node->r = LL(node->r); // Convert to rr case
node = ReColor(node, false); // Resolution feature 4)
node = RR(node); // Resolution feature 5)
}
}
}
weight = 0;
break;
// At this time, the black length of the left subtree is reduced by 1
case -2:
/*
* Let the black node length of the left and right subtrees of the current node L=R=n
* At this time, the left subtree L=n-1,R=n
* In order to balance the left and right, there are two schemes:
* 1)The right sub black node is transferred to the left sub tree by rotation, and a red node is blackened at the same time.
* 2)Color a black node of the right subtree red and recurse upward.
*/
if (node->r->r != nullptr && isRed(node->r->r)) { // Option 1)
node = RR(node);
// Swap parent and right node colors
node->color = node->l->color;
node->l->color = BLACK;
// Black red color
node->r->color = BLACK;
// Set equilibrium constant to zero
weight = 0;
} else if (node->r->l != nullptr && isRed(node->r->l)) { // Option 1)
node->r = LL(node->r);
node = RR(node);
// Swap parent and right node colors
node->color = node->l->color;
node->l->color = BLACK;
// Black red color
node->r->color = BLACK;
// Set equilibrium constant to zero
weight = 0;
} else if (isRed(node->r)) {
node = RR(node);
// Swap parent and right node colors
node->color = BLACK;
node->l->color = RED;
node->l = rebalance(node->l, weight);
} else if (isRed(node->r) == false) { // Both the right node and the right child node are black
node->r->color = RED;
if (isRed(node)) { // Parent node red
node->color = BLACK;
weight = 0;
} else { // Parent node black scheme 2)
weight = -1;
}
}
break;
case 2: // Black length of right subtree minus 1
if (node->l->l != nullptr && isRed(node->l->l)) { // Option 1)
node = LL(node);
// Swap parent and right node colors
node->color = node->r->color;
node->r->color = BLACK;
// Black red color
node->l->color = BLACK;
// Set equilibrium constant to zero
weight = 0;
} else if (node->l->r != nullptr && isRed(node->l->r)) { // Option 1)
node->l = RR(node->l);
node = LL(node);
// Swap parent and right node colors
node->color = node->r->color;
node->r->color = BLACK;
// Black red color
node->l->color = BLACK;
// Set equilibrium constant to zero
weight = 0;
} else if (isRed(node->l)) {
node = LL(node);
// Swap parent and right node colors
node->color = BLACK;
node->r->color = RED;
node->r = rebalance(node->r, weight);
} else if (isRed(node->l) == false) { // Nodes and child nodes are black
node->l->color = RED;
if (isRed(node)) { // Parent node red
node->color = BLACK;
weight = 0;
} else { // Parent node black scheme 2)
weight = -1;
}
}
break;
default:
break;
}
return node;
}
/*
* There are four situations for red black tree insertion:
* 1) Leaf node
* 2) There are left subtrees
* 2-1) Delete node red - child node black, not conforming to characteristic 5)
* 2-2) Delete node black - child node red
* 3) There is a right subtree
* 3-1) Delete node red - child node black, not conforming to characteristic 5)
* 3-2) Delete node black - child node red
* 4)There are left and right subtrees, and the deleted node is replaced by the precursor node (K,V) to delete the precursor node. 1) 2)
*/
RBNode *remove(RBNode *node, K key, int &weight) {
if (node == nullptr) return nullptr;
RBNode *_new = nullptr;
if (key < node->key) {
node->l = remove(node->l, key, weight);
_new = node;
weight = (weight == -1) ? -2 : 0; //
} else if (key > node->key) {
node->r = remove(node->r, key, weight);
weight = (weight == -1) ? 2 : 0; //
_new = node;
} else {
if (node->l == nullptr) {
_new = node->r;
if (_new != nullptr) { // 3-2)
_new->p = node->p;
_new->color = BLACK;
} else if (node->color == BLACK) {
weight = -1; // 1) Delete node is black
} else {
; // 1) The current node is red
}
} else if (node->r == nullptr) {
_new = node->l; // 2-2)
_new->p = node->p;
_new->color = BLACK;
} else { // 4)
_new = Max(node->l); // Find the precursor node in the left subtree
_new->l = remove(node->l, _new->key, weight);
_new->p = node->p;
_new->r = node->r;
_new->color = node->color;
if(_new->l != nullptr)
_new->l->p = _new;
if(_new->r != nullptr)
_new->r->p = _new;
weight = (weight == -1) ? -2 : 0;
}
}
return rebalance(_new, weight);
}
RBNode *root;
#ifdef _DEBUG
int Check(RBNode *node) {
if (node == nullptr)
return 1;
else {
if (isRed(node) && isRed(node->p)) return -1;
if (node->l != nullptr && node != node->l->p) return -1;
if (node->r != nullptr && node != node->r->p) return -1;
int left = Check(node->l);
int right = Check(node->r);
if (left == -1 || right == -1 || left != right) return -1;
if (node->color == RED)
return left;
else
return left + 1;
}
}
#endif
public:
RBTree() { root = nullptr; }
~RBTree() { DelNode(root); }
void add(K key, V data) {
RBNode *node = get(root, key);
if (node != nullptr) return;
int weight = 0;
root = add(root, root, key, data, weight);
}
V get(int key) {
RBNode *node = get(root, key);
if (node != nullptr) return node->val;
return nullptr;
}
#ifdef _DEBUG
int Check() { return Check(root); }
#endif
V remove(int key) {
RBNode *node = get(root, key);
if (node == nullptr) return 0;
V val = node->val;
int weight = 0;
root = remove(root, key, weight);
delete node;
return val;
}
};