lookup

sequential search

Sequential lookup of unordered tables

def sequentialSearch(alist, item):
    pos = 0
    found = False
    while pos < len(alist) and not found:
        if alist[pos] == item:
            found = True
        pos += 1
    return found

testlist = [3, 8, 5, 9, 7]
print(sequentialSearch(testlist,5))

Sequential lookup of ordered tables

def orderedSequentialSearch(alist,item):
    pos = 0
    found = False
    stop = False
    while pos < len(alist) and not found and not stop:
        if alist[pos] == item:
            found = True
        if alist[pos] > item:
            stop = True
        pos += 1
    return found

testlist = [10, 20, 30, 40, 50, 60, 70]
print(orderedSequentialSearch(testlist,35))

Two point search

It is also a divide and conquer strategy, which is to split the ordered table into two parts and search in a small range after splitting.

def binarySearch(alist,item):
    first = 0
    found = False
    last = len(alist) - 1

    while first <= last and not found:
        print(first, last)
        midPos = (first + last) // 2
        if item == alist[midPos]:
            found = True
        else:
            if item < alist[midPos]:
                last = midPos - 1
            else:
                first = midPos + 1
    return found

testlist = [10, 20, 30, 40, 50, 60, 70]
print(binarySearch(testlist, 35))

Recursive solution of binary search

def binarySearch2(alist,item):
    if len(alist) == 0:
        return False
    else:
        midPos = len(alist) // 2
        if item == alist[midPos]:
            return True
        else:
            if item < alist[midPos]:
                binarySearch2(alist[:midPos], item)
            else:
                binarySearch2(alist[midPos+1:], item)

testlist = [10, 20, 30, 40, 50, 60, 70]
print(binarySearch2(testlist, 20))

sort

Bubble sort

The time complexity of bubbling method is O(n^2)

def bubbleSort(alist):
    for passnum in range(len(alist)-1,0,-1):
        for i in range(passnum):
            if alist[i] > alist[i+1]:
                alist[i+1], alist[i] = alist[i], alist[i+1]
testlist = [3, 8, 5, 9, 7]
bubbleSort(testlist)

An optimization scheme of bubble sorting

def bubbleSort2(alist):
    exchange = True
    passnum = len(alist) - 1
    while passnum > 0 and exchange:
        exchange = False
        for i in range(passnum):
            if alist[i] > alist[i+1]:
                alist[i+1], alist[i] = alist[i], alist[i+1]
                exchange = True
testlist = [3, 8, 5, 9, 7]
bubbleSort2(testlist)
print(testlist)

Selection sort

Selective sorting is an evolution of bubbling. The time complexity of comparison is O(n^2), and the time complexity of exchange is O(n), which only reduces the number of exchanges.

def selectionSort(alist):
    i = 0
    while i < len(alist):
        j = i + 1
        minIndex = i
        while j < len(alist):
            if alist[j] < alist[minIndex]:
                minIndex = j
            j += 1
        alist[i], alist[minIndex] = alist[minIndex], alist[i]
        i += 1

testlist = [3, 8, 5, 9, 7]
selectionSort(testlist)
print(testlist)

Another solution to the choice of sorting:

def selectionSort2(alist):
    for passnum in range(len(alist)-1, 0, -1):
        maxIndex = 0
        for i in range(passnum):
            if alist[i + 1] > alist[maxIndex]:
                maxIndex = i + 1
        alist[passnum], alist[maxIndex] = alist[maxIndex], alist[passnum]

testlist = [3, 8, 5, 9, 7, 2]
selectionSort2(testlist)
print(testlist)

Insertion sort

The complexity of inserting a collation size is still O(n^2), but the performance will be slightly better. Insertion sorting will compare the value of the previous position with the value to be inserted each time; if it is larger than the value to be inserted, it will move the previous position backward; otherwise, it will break the comparison size and insert the current value into this position. So if the list itself is ordered, the number of times it compares is greatly reduced.

def insertSort(alist):
    for index in range(1, len(alist)):
        currentValue = alist[index]
        position = index
        while position > 0 and alist[position - 1] > currentValue:
            if alist[position - 1] > currentValue:
                alist[position] = alist[position - 1]
            position -= 1
        alist[position] = currentValue

testlist = [3, 8, 5, 9, 7, 2]
insertSort(testlist)
print(testlist)

Schell sort

Schell (Hill) sort divides the original list into multiple sub lists with each two elements as a group, and then inserts the sort to the sub list; then divides the original list into multiple sub lists with each four elements as a group, and then inserts the sort to the sub list;... Inserts the sort until the original list is divided into a single sub list, and finally obtains the final result. The general interval settings are from n/2, n/4, n/8... To 1. The number of invalid comparisons is greatly reduced, and the complexity is between O(n) and O(n^2), about O (n ^ 3 / 2)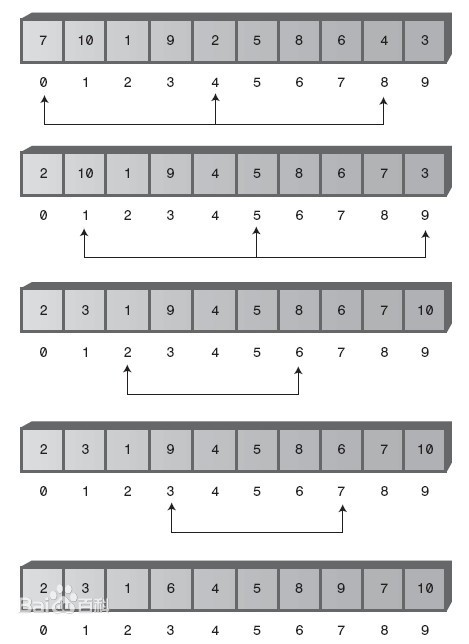

def shellSort(alist):
    sublistcount = len(alist) // 2. Set interval
    while sublistcount > 0:
        for startposition in range(sublistcount):
            gapInsertionSort(alist, startposition, sublistcount)
        sublistcount = sublistcount // 2. Reducing the interval

def gapInsertionSort(alist, start, gap):         #This function sorts the sublist
    for i in range(start + gap, len(alist), gap):
        currentValue = alist[i]
        position = i
        while position >= gap and alist[position - gap] > currentValue:
            alist[position] = alist[position - gap]
            position = position - gap
        alist[position] = currentValue

testlist = [3, 8, 5, 9, 7, 2]
shellSort(testlist)
print(testlist)

Merge sort

Merge sorting is a kind of divide and conquer strategy. It continuously splits the original list, and then sorts the two parts separately after splitting, and then merges them. It is a recursive idea. The time complexity is O(n), but it wastes twice the storage space.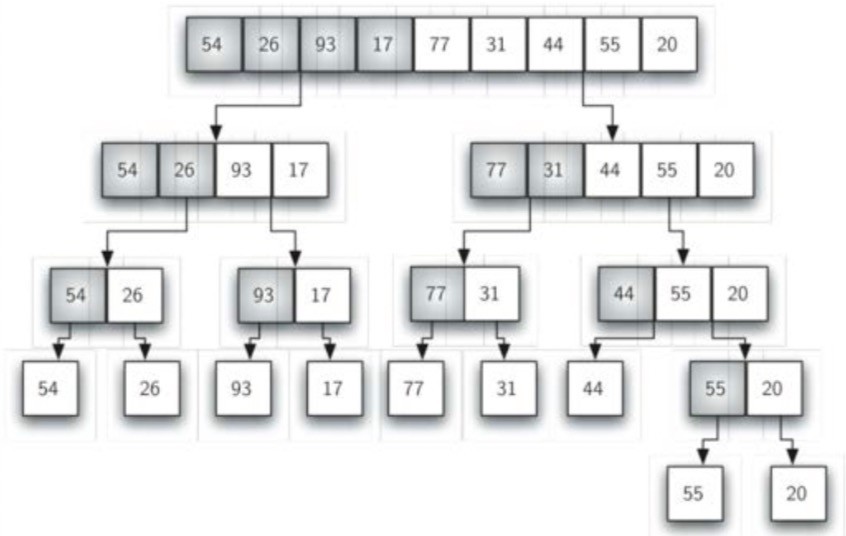

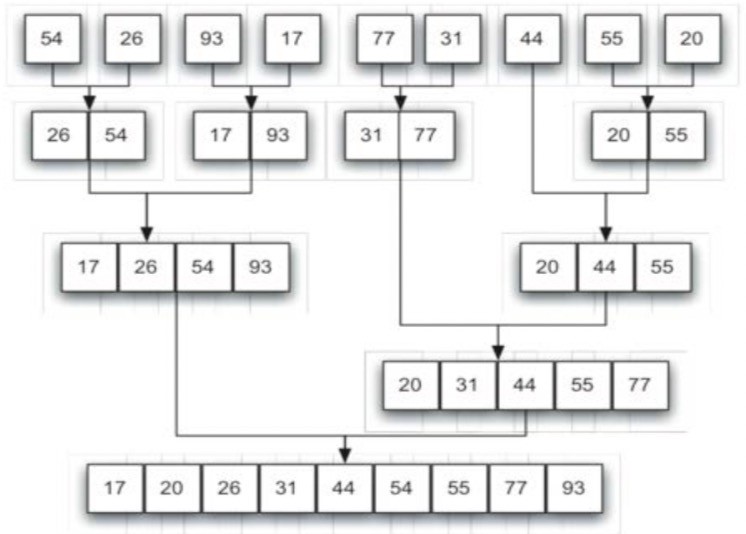
def mergeSort(alist):
    if len(alist) > 1:
        mid = len(alist) // 2
        lefthalf = alist[:mid]
        righthalf = alist[mid:]

        mergeSort(lefthalf)
        mergeSort(righthalf)

        i = j = k = 0
        while i < len(lefthalf) and j < len(righthalf):
            if lefthalf[i] < righthalf[j]:
                alist[k] = lefthalf[i]
                i += 1
            else:
                alist[k] = righthalf[j]
                j += 1
            k += 1

        while i < len(lefthalf):
            alist[k] = lefthalf[i]
            i += 1
            k += 1

        while j < len(righthalf):
            alist[k] = righthalf[j]
            j += 1
            k += 1

testlist = [3, 8, 5, 9, 7, 2]
mergeSort(testlist)
print(testlist)

Recursive solution of merging and sorting:

def merge_sort(alist):
    if len(alist) <= 1:
        return alist
    mid = len(alist) // 2
    left = alist[:mid]
    right = alist[mid:]
    return merge(merge_sort(left), merge_sort(right))

def merge(left, right):
    result = []
    while left and right:
        if left[0] <= right[0]:
            result.append(left.pop(0))
        else:
            result.append(right.pop(0))
    result.extend(right if right else left)
    return result

# testlist = [3, 8, 5, 9, 7, 2]
# print(merge_sort(testlist))

Quick sort

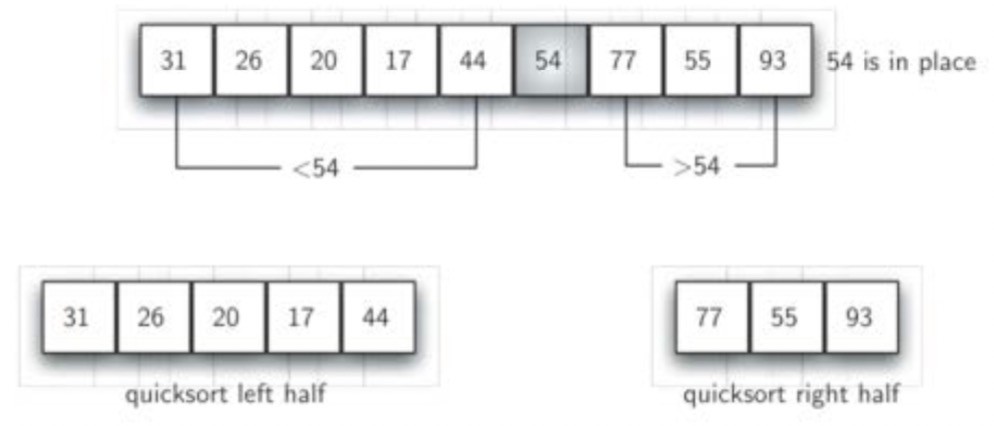
Quick sort divides the original list into two parts (sorting and splitting) based on a "median" data item, and then sorts each part quickly.
The goal of the split is to find the "median", and the specific operations are as follows:

• Set the right side (next) of the first item to leftmark; set the left side (previous) to rightmark;
• Then the leftmark moves to the right, when it is larger than the first value, stop; rightmark moves to the left, when it is smaller than the first value, stop;
• Then data exchange between leftmark and rightmark;
• Then the leftmark and rightmark continue to move until the leftmark moves to the right of the rightmark;
• At this time, the location of rightmark should be the location of "median", and then exchange the first item with the data of rightmark;
  If splitting can divide the data table into two equal parts, the complexity of splitting is O(logN); in extreme cases, its complexity will degenerate to O(n^2). The complexity of the whole comparison and movement is O(n); no additional storage space is needed in the whole process.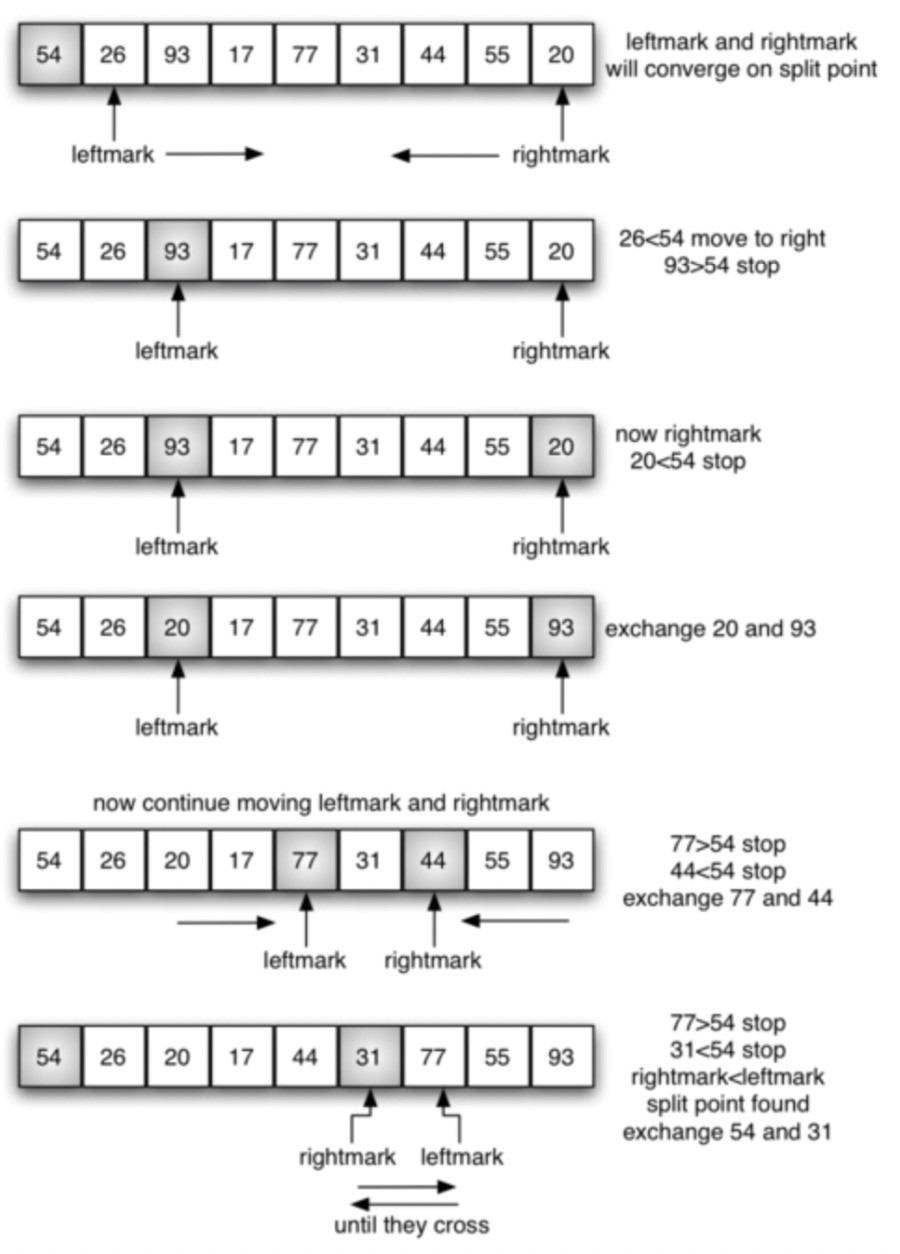
  
  

def partition(alist, first, last):
    pivotvalue = alist[first]

    leftmark = first + 1
    rightmark = last

    done = False
    while not done:
        while leftmark <= rightmark and alist[leftmark] <= pivotvalue:
            leftmark = leftmark + 1

        while rightmark >= leftmark and alist[rightmark] >= pivotvalue:
            rightmark = rightmark -1

        if rightmark < leftmark:
            done = True
        else:
            alist[leftmark], alist[rightmark] = alist[rightmark], alist[leftmark]
    alist[first], alist[rightmark] = alist[rightmark], alist[first]

    return rightmark  # At this time, rightmark points to the split point

def quickSortHelper(alist, first, last):
    if first < last:  # There must be at least two elements in the list to split
        splitpoint = partition(alist, first, last)
        quickSortHelper(alist, first, splitpoint - 1)
        quickSortHelper(alist, splitpoint + 1, last)

def quickSort(alist):
    quickSortHelper(alist, 0, len(alist)-1)

testlist = [3, 8, 5, 9, 7, 2]
quickSort(testlist)
print(testlist)