Chapter VI diagram

1. Basic structure of the drawing

1.1 basic concept of drawing

1) Graph G (graph) is composed of Vertex set V (Vertex) and Edge set E (Edge), which is marked as G=(V,E), where V(G) represents the finite nonempty set of vertices in graph G;
E(G) represents the set of relationships (edges) between vertices in graph G. If V={v1,v2..., vn}, use | V | to represent the number of vertices in graph G, also known as the order of graph G, E= {(u, v)| u ∈ U, v ∈ V}, and use | e | to represent the number of edges in graph G.

Note: the linear table can be an empty table and the tree can be an empty tree, but the graph cannot be empty, that is, V must be a non empty set and U can be an empty set.

2) Simple graph: there are no duplicate edges; There is no vertex to its own edge. (only simple pictures)
Multigraph: if there are more than one edge between two nodes in graph G, and vertices are allowed to associate with themselves through the same edge, then G is a multigraph

3) Undirected graph and directed graph

i. Undirected graph: if E is a finite set of undirected edges, then graph G is an undirected graph. Edges are unordered pairs of vertices, labeled (v,w) or (w, v), because (w, v) = (v,w), where V and W are vertices. It can be said that vertex W and vertex v are adjacent to each other. Edges (v,w) are attached to vertices W and V, or edges (v,w) are associated with vertices V and W.

Degree: the degree of vertex v refers to the number of edges attached to the vertex, which is recorded as TD(v); The sum of the degrees of all fixed points is twice the number of vertices.

ii. Directed graph: if E is a finite set of directed edges (also known as arcs), then graph G is a directed graph. An arc is an ordered pair of vertices, which is recorded as < V, w >, where V and W are vertices, V is called the arc tail, W is called the arc head, < V, w > is called the arc from vertex v to vertex W, also known as adjacent to W, or W is adjacent to v< v, w> ≠ <w, v>

In degree is the number of directed edges ending at vertex v, which is recorded as ID(v);
Out degree is the number of directed edges starting from vertex v, which is recorded as OD(v).
Sum of in degrees = sum of out degrees = number of vertices

4) Vertex vertex relationship description

Path: a path from vertex a to vertex b refers to a sequence of vertices;
Loop: the same path between the first vertex and the last vertex is called a loop or ring;
Simple path: in the path sequence, the path whose vertices do not appear repeatedly is called simple path;
Simple loop: a loop in which no vertices are repeated except the first vertex and the last vertex is called a simple loop;
Path length: the number of edges on the path;
Distance from point to true: if the shortest path from vertex u to vertex v exists, the length of this path is called the distance from u to v. if there is no path from u to V, the distance is recorded as infinite;
Connectivity: in an undirected graph, if there is a path from vertex v to vertex w, then V and w are connected; If any two vertices in graph G are connected, graph G is called connected graph, otherwise it is called unconnected graph.
Strongly connected: in a directed graph, if there are paths from vertex v to vertex W and from vertex w to vertex v, the two vertices are said to be strongly connected; If any pair of vertices in a graph are strongly connected, the graph is called strongly connected.

Frequent test sites:

For an undirected graph G with n vertices, if G is a connected graph, there are at least n-1 edges, and if G is a non connected graph, there may be at most C2n-1 edges.
For a directed graph with n vertices, if G is a strongly connected graph, there are at least n edges to form a loop.

5) Study the local of Graphs

There are two graphs G= (V, E) and G '= (v', e '). If v is a subset of v and E' is a subset of E, G 'is said to be a subgraph of G.

If there is a subgraph G 'satisfying v(G') = v(G), it is called the generated subgraph of G.

The polar Dalian pass subgraph of an undirected graph is called connected component. The polar Dalian pass subgraph should contain as many vertices and edges as possible.
The maximal strongly connected subgraph in a directed graph is called the strongly connected component of a directed graph

Spanning tree: the spanning tree of a connected graph is a minimal connected subgraph containing all vertices in the graph. N vertices, n-1 edges.

Spanning forest: in a non connected graph, the spanning tree of connected components constitutes the spanning forest of a non connected graph.

6) Weighted graph / net of edges

Edge weight: in a graph, each edge can be marked with a value with some meaning, which is called the weight of the edge.
Weighted graph / net: the graph with weight on the edge is called weighted graph, also known as net.
Weighted path length: when the graph is a weighted graph, the sum of the weights of all edges on a multi-path is called the weighted path length of the path.

7) Graphs of several special forms

Undirected complete graph: there are edges between any two vertices in an undirected graph, v = n, e = C2n;
Directed complete graph: there are two arcs with opposite directions between any two vertices in a directed graph, v=n, e=2C2n;
Sparse graph and dense graph: Generally speaking, when | e < | V | log | V |, G can be regarded as a sparse graph, otherwise it is a dense graph;
Tree: connected undirected graph without loop, v=n, e=n-1; If there are k trees in the forest, e=v-k
Directed tree: a directed graph in which the penetration of one vertex is 0 and the penetration of other vertices is 1 is called a directed tree.

1.2 storage of drawings

1.2.1 adjacency matrix

The representation method is unique.

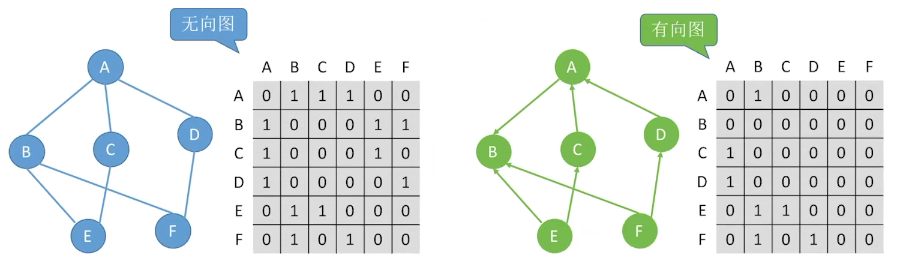
An undirected graph is a symmetric matrix and can only save the upper triangle.

#define MaxVertexNum 100 					// Maximum number of vertices
typedef struct{
	char Vex[MaxVertexNum];					//Vertex table
	bool Edge[MaxVertexNum][MaxVertexNum];	//Adjacency matrix, edge table
    int Vexnum,arcnum;						//The current number of vertices and edges / arcs of the graph
}MGraph;
//Correspondence between one-dimensional array and two-dimensional array: (I, J) - > k
//k = i * n +j -> i = k / n, j = k % n;

Undirected graph: the degree of the ith node = the number of non-zero elements in row i (or column i); O(n)；
Digraph: the degree of the ith node = the number of non-zero elements in the ith row;
Penetration = number of non-zero elements in column i;
The ith degree = the sum of the number of non-zero elements in row i and column i

Storage belt weight diagram:

#define MaxVertexNum 100 			// Maximum number of vertices
#define INFINITY 0x3f3f3f3f 			// Macro defines the constant "infinity" 0xc0c0c0c0 c0 as infinitesimal
typedef char VertexType;			//Data type of vertex
typedef int EdgeType;				//Data types of edge weights in Weighted Graphs
typedef struct{
	VertexType Vex [MaxVertexNum];	//vertex
	EdgeType Edge [MaxVertexNum][MaxVertexNum];//Edge weight
    int vexnum,arcnum;				//Current vertex number and arc number of graph
}MGraph;
//Generally, you only want to record your rights as 0;

It is suitable for storing dense graphs. The space complexity is related to the number of vertices.

nature:
Let the adjacency matrix of graph G be A (the matrix element is 0 / 1, order n), then the element A[i][j] of An is equal to the number of paths with length n from vertex i to vertex j. For example, the number of path trees with path length of 2 from 1 to 4 is as follows:

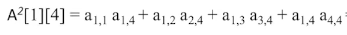
Test site:

i. How to calculate the degree, in degree and out degree of a specified vertex (divided into undirected graph and directed graph);
ii. What is the time complexity? How to find the edge (in edge, out edge) adjacent to the vertex? Time complexity;
iii. how to store the weight map;
iv. the spatial complexity is O(|v|2), which is suitable for storing dense graphs;
v. The adjacency matrix of an undirected graph is a symmetric matrix;
vi. let the adjacency matrix of graph G be A (the matrix element is 0 / 1), then the element A[i][j] of An is equal to the number of paths with length n from vertex i to vertex j.

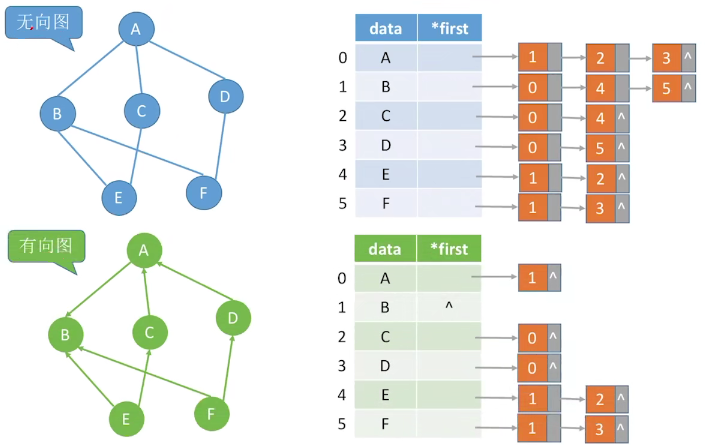
1.2.2 adjacency table

Sequential storage + chain storage, similar to the "child brother" representation of a tree
The representation method is not unique

#define MaxVertexNum 100 			// Maximum number of vertices
//Edge / arc“
typedef struct(ArcNode{
	int adjvex;					//Which node does the edge / arc point to
	struct ArcNode *next;		//Pointer to the next arc
	//infoType info; 			// Edge weight
}ArcNode;
//vertex
typedef struct VNode {
    VertexType data;		//Vertex information
    ArcNode *first;			//First edge / arc
}VNode， AdjList[MaxVertexNum];
//Graph stored with adjacency table
typedef struct {
    AdjList vertices;
    int vexnum, arcnum;
}ALGraph;

In an undirected graph, the number of edge nodes is 2e and the overall spatial complexity is O(v+2e); in a directed graph, the number of edge nodes is e and the overall spatial complexity is O(v+e)
The degree of an undirected graph and the degree of penetration of a directed graph only need to traverse the linked list of the node, and the degree of penetration of a directed graph needs to traverse the whole adjacency list.

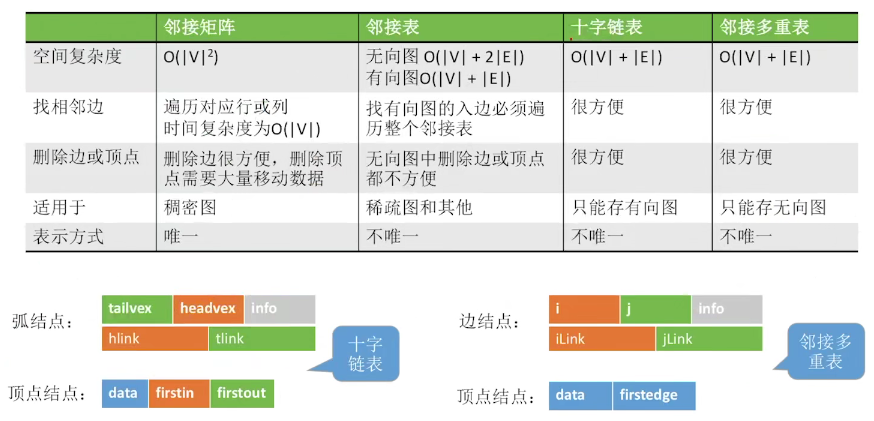
1.2.3 cross linked list

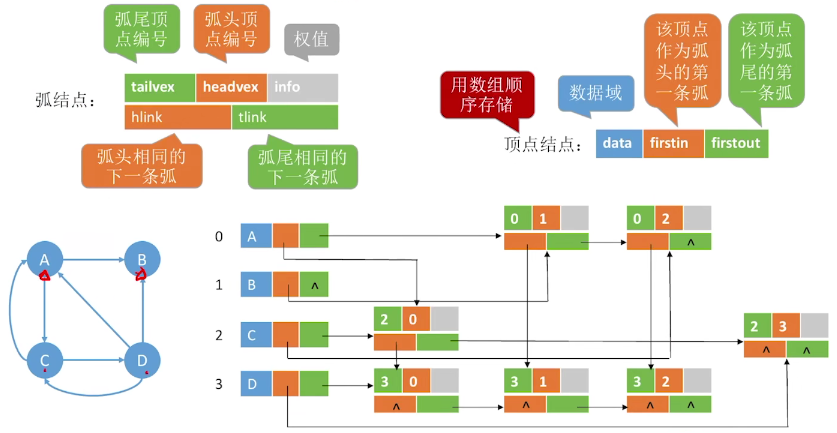
You can find the degree along the tlink pointer and the degree along hlink. The cross linked list method is only used to store directed graphs.

1.2.4 adjacency multiple table

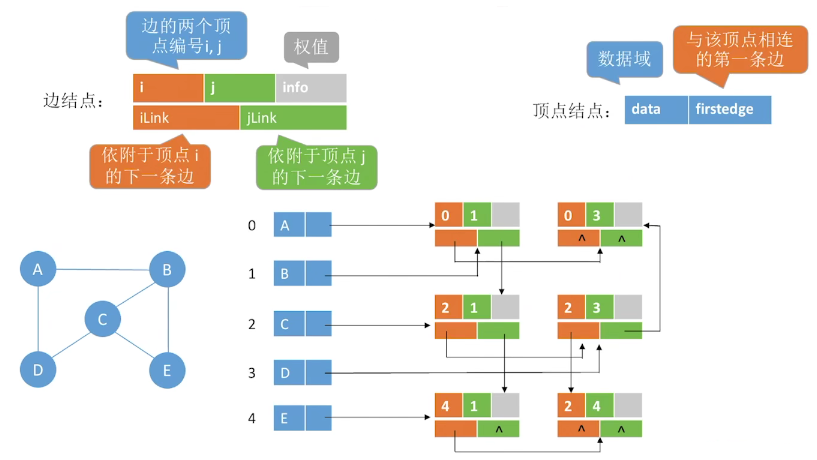
Spatial complexity: O(v+e). It is convenient to delete edges and nodes. Adjacency multiple tables are only suitable for storing undirected graphs.

Summary:

6.3 basic operation

Directed graphs are stored by adjacency matrix and undirected graphs by adjacency table.

Basic operation of the diagram:
Adjacent(G,x,y):Judgment diagram G Is there an edge<x, y>or(x, y). 
Neighbors(G,x):List diagram G Middle and node x Adjacent edges.
lnsertVertex(G,x):In Figure G Insert vertex in x. 
DeleteVertex(G,x):From figure G Delete vertices from x. 
AddEdge(G,x,y):If undirected edge(x,y)Or directed edge<x, y>If it does not exist, it is directed to the graph G Add the edge to the.
RemoveEdge(G,x,y):If undirected edge(x,y)Or directed edge<x, y>If it exists, start from the figure G Delete the edge from the.
Get_edge_value(G,x,y):Get graph G Middle edge(x, y)or<x, y>Corresponding weight.
set_edge_value(G,x,yv):Setting diagram G Middle edge(x, y)or<x, y>The corresponding weight is v. 
//Note the implementation difference between directed graph and undirected graph
FirstNeighbor(G,x):Graph seeking G Middle vertex x The first adjacent contact, if any, returns the vertex number x There are no adjacency points or do not exist in the graph x，Then return-1. 
NextNeighbor(G,x,y):Hypothesis diagram G Middle vertex y Is the vertex x An adjacent contact of returns division y Outer vertex x Vertex number of the next adjacent contact of, if y yes x The last adjacent contact of the-1. 

2. Graph traversal

2.1 breadth first traversal (BFS)

The hierarchical traversal of a tree is a breadth first traversal.

Key points of breadth first search (BFS):
i. Find all vertices adjacent to a vertex: FirstNeighbor(G,x), NextNeighbor(G,x,y)
ii. Mark which vertices have been accessed: define the access mark array to record whether they have been accessed.
iii. a secondary queue is required

bool visited [MAX_VERTEX_NUM];//Access tag array
void BFSTraverse(Graph G){		//Breadth first traversal of graph G
	for(i=0; i<G.vexnum; ++i)
		visited[i]=FALSE;		//Access tag array initialization
	InitQueue(Q);				//Initialize auxiliary queue Q
	for(i=0; i<G.vexnum; ++i)	//Traverse from vertex 0
		if(!visited[i])			//BFS is called once for each connected component
			BFS(G,i);			//vi not visited, BFS started from vi
}
//breadth-first search 
void BFS(Graph G,int v){			//Starting from vertex v, breadth first traverses graph G
	visit(v);						//Access initial vertex v
	visited[v]=TRUE;				//Mark v as accessed
	Enqueue(Q,v);					//Vertex v into queue Q
	while(!isEmpty(Q)){
	DeQueue(Q,v);					//Vertex v out of queue
	for(w=FirstNeighbor(G,v);w>=0; w=NextNeighbor(G,v,w)){
			//Detect v all adjacency points
			if(!visited[w]){		//Adjacent vertices not yet accessed with w as v
				visit(w);			//Access vertex w
				visited[w]=TRUE;	//Mark w as accessed
        		EnQueue(Q,w);		//Vertex w in queue
        	}//fi
    	}//rof
	}//elihw
}

For undirected graphs, the number of calls to the BFS function = the number of connected components

Space complexity: O(v), time complexity: adjacency matrix needs O(v2), adjacency table needs O(v+e)

Breadth first spanning tree (forest): it is generated according to the breadth first process.

Focus: find breadth first traversal sequence

2.2 depth first traversal (DFS)

The first root traversal of a tree is a depth first traversal.

bool visited [MAX_VERTEX_NUM] ;	//Access tag array
void DFSTraverse(Graph G){		//Depth first traversal of figure G
	for(i=0; i<G.vexnum; ++i)
		visited[i]=FALSE;		//Access tag array initialization
	for(i=0; i<G.vexnum; ++i)	//Traverse from vertex 0
		if(!visited[i])			//DFS is called once for each connected component
			DFS(G,i);			//vi has not been accessed, DFS started from vi
}

void DFS(Graph G,int v){			//Starting from vertex v, depth first traverses graph G
	visit(v);						//Access vertex v
	visited[v]=TRUE;				//Set accessed flag
	for(w=FirstNeighbor(G,v); w>=0; w=NextNeighor(G,v,w)){
		if (!visited[w]){			//Adjacent vertices not yet accessed with w as u
			DFS(G,w);
		}//fi
    }//rof
}

Space complexity: best O(1), worst O(v), time complexity: adjacency matrix needs O(v2), adjacency table needs O(v+e)

Focus: find the depth first traversal sequence

3. Application of diagram (key points)

3.1 minimum spanning tree

For a weighted connected undirected graph G =(V, E), the spanning tree is different, and the weight of each tree (i.e. the sum of the weights on all edges in the tree) may also be different. Let R be the set of all spanning trees of G. if T is the spanning tree with the smallest sum of the weights of edges in R, 7 it is called the minimum spanning tree (MST) of G.

be careful:
i. There may be multiple minimum spanning trees, but the sum of the weights of the edges is always unique and minimum
ii. The number of edges of the minimum spanning tree = the number of vertices - 1. If one edge is cut off, it will not be connected, and if one edge is added, a loop will appear
iii. If a connected graph itself is a tree, its minimum spanning tree is itself
iv. only connected graphs have spanning trees, and non connected graphs only have spanning forests

3.1.1 general algorithm:

GenericMst(G){
	T = Ø;
    while(T A spanning tree is not formed){
        Find a minimum cost edge(u,v)；
            if((u,v)join T No ring will be formed after)
                T = T ∪ (u,v);
    }
}

3.1.2 Prim algorithm (PRIM):

(select points) build the spanning tree from a vertex; each time the least expensive new vertex is included in the spanning tree until all vertices are included.

The time complexity is O(v2), which is suitable for edge dense graphs.

void Prim(G,T){
	T = Ø;						//Initialize empty tree
    U = {w};					//Add any vertex w
    while((V-U) != Ø){			//If the tree does not contain all vertices
        set up(u,v),satisfy u∈U， v∈(V-U),And is the edge with the smallest weight;
        T = T ∪ {(u,v)};		//Add this edge to the spanning tree
        U = U ∪ {v};			//Vertex attributed tree
    }
}

Two arrays need to be defined:
isJoin[v] mark whether each node has joined the tree,
lowCost[v] the lowest cost for each node to join the tree. If it cannot join directly, it is recorded as (∞)

You can continue to optimize and mark

3.1.3 Kruskal algorithm (Kruskal)

(edge selection) select an edge with the smallest weight each time to connect the two ends of this edge (those already connected are not selected)
Until all nodes are connected.

Time complexity: O(e*log2e), suitable for edge sparse graphs.

void Kruskal(V,T){
	T = V;						//Initialize tree T, containing only vertices
    numS = n;					//Connected component number
    while(numS > 1){			//If the connected component is greater than 1
        from E The edge with the smallest weight is extracted from the(v,u);
        if(v and u belong to T Different connected components in){
        	T = T ∪ {(u,v)};		//Add this edge to the spanning tree
        	numS = numS - 1;		//Connected component minus one
        }
    }
}

You need to sort all vertices according to their weights, using Joint search set Judge whether it belongs to the same connected component.

3.2 shortest path problem

3.2.1 single source shortest path problem:

BFS algorithm (weighted graph)

bool visited [MAX_VERTEX_NUM];//Access tag array
void BFSTraverse(Graph G){		//Breadth first traversal of graph G
	for(i=0; i<G.vexnum; ++i)
		visited[i]=FALSE;		//Access tag array initialization
	InitQueue(Q);				//Initialize auxiliary queue Q
	for(i=0; i<G.vexnum; ++i)	//Traverse from vertex 0
		if(!visited[i])			//BFS is called once for each connected component
			BFS(G,i);			//vi not visited, BFS started from vi
}
//breadth-first search 
void BFS(Graph G,int v){			//Starting from vertex v, breadth first traverses graph G
	//visit(v); 						// Access initial vertex v
    for(i=0; i<G.vexnum ;++i){		//d[i] represents the shortest path from u to I node
        d[i]=0x3f3f3f3f;			//Initialization path length
		path[i]=-1;					//Which vertex does the shortest path come from
	}
	d[v] = 0;
	visited[v]=TRUE;				//Mark v as accessed
	Enqueue(Q,v);					//Vertex v into queue Q
	while(!isEmpty(Q)){				//BFS algorithm core
	DeQueue(Q,v);					//Vertex v out of queue
	for(w=FirstNeighbor(G,v);w>=0; w=NextNeighbor(G,v,w)){
			//Detect v all adjacency points
			if(!visited[w]){		//Adjacent vertices not yet accessed with w as v
				//visit(w); 			// Access vertex w
                d[w] = d[v] + 1;	//Path length plus one
                path[w] = v;		//The shortest path should be from u to w
				visited[w]=TRUE;	//Mark w as accessed
        		EnQueue(Q,w);		//Vertex w in queue
        	}//fi
    	}//rof
	}//elihw
}

Dijkstra algorithm (weighted graph, non weighted graph) (key)

Put forward "goto harmful theory" - an operating system, virtual storage technology
Semaphore mechanism PV primitive 1 - operating system, process synchronization
Banker algorithm -- operating system, deadlock
Solve the dining problem of philosophers - operating system, deadlock
Dijkstra shortest path algorithm -- large and small problems of data structure

Algorithm idea: similar to Prime algorithm, greedy

Two auxiliary arrays:
dist []: record the current shortest path length from the source point v0 to other vertices;
path[i]: represents the precursor node of the shortest path from the source point to vertex I

If from V0 Start, make final[0]=ture; dist[0]=0; path[0]=-1;
Remaining vertices final[k]=false; dist[k]=arcs[0][k];
path[k]=arcs[0][k]<INF? 0 ∶-1
 Loop through all vertices to find the shortest path that has not been determined, and dist Smallest vertex Vi，order final[i]=ture. 
And check all adjacent from Vi For vertices adjacent from Vi Vertex of Vj，
if final[i]==false And dist[i]+arcs[i][j]< dist[j]，
Then order dist[j]=dist[i]+arcs[i][i]; path[j]=i. 
(notes: arcs[i][j]express Vi reach Vj Weight of arc)

#include <iostream>
#define Max 503
#define INF 0x3f3f3f3f 								// Macro definition infinity
using namespace std;
typedef struct MGraph {								//Definition diagram
	int vex, arc;									//Number of vertices, number of edges
	int arcs[Max][Max];								//adjacency matrix 
}MGraph;

int dist[Max], path[Max];							//dist saves the total weight and path of the shortest path, and saves the path through the precursor node of the path
bool final[Max];									//Shortest path set found
void Dijkstra(MGraph &G)							//Dijkstra's algorithm 
{
	for (int i = 1; i <= G.vex; i++)				
	{
		dist[i] = G.arcs[0][i];						//Initialize dist array
		path[i] = dis[i] < INF ? 0 : -1;			//Initialize path array
	}
	final[0] = true;									
	dist[0] = 0;									//Starting point initialization
	for (int i = 1; i < G.vex; i++)					//Traverse G.vex-1 times
	{
		int mins = INF, u = 0;
		for (int j = 1; j < G.vex; j++)				//Find the shortest backdrive point that is not currently added to the set
		{
			if (!final[j] && mins > dist[j]) {
				mins = dist[j];
				u = j;
			}
		}
		final[u] = true;							//Add the point to the collection
		for (int j = 1; j <= G.vex; j++)			//Traverse all other points to update their shortest path (relaxation operation)
		{
			if (!final[j] && dist[j] > dist[u] + G.arcs[u][j]) {
				dist[j] = dist[u] + G.arcs[u][j];	//Update shortest path value
				path[j] = u;						//The precursor of modified j is u
			}
		}
	}
}
void find(int x)									//Recursive output shortest path
{
	if (path[x] == 1) {
		cout << 1;
	}
	else {
		find(path[x]);
	}
	cout << " -> " << x;
	return;
}
void input(MGraph &G)								//Input diagram
{
	cin >> G.vex >> G.arc;
	for (int i = 1; i <= G.vex; i++)				//Initialize adjacency matrix
		for (int j = 1; j <= G.vex; j++)
			G.arcs[i][j] = INF;

	for (int i = 1; i <= G.arc; i++)			
	{
		int u, v, w;
		cin >> u >> v >> w;
		G.arcs[u][v] = w;
	}
}
void output(MGraph &G)								//output
{
	//Cout < < "the shortest distance from the starting point v1 to each point is: \ n";
	for (int i = 1; i < G.vex; i++)
	{
		cout << dist[i] << " ";
	}
	cout << dis[G.vex] << endl;
	/*for (int i = 2; i <= G.vex; i++)
	{
		cout << "The path from the starting point v1 to V "< < I < <" is: ";
		find(i);
		cout << endl;
	}*/
}
int main()
{
	MGraph G;
	input(G);
	Dijkstra(G);
	output(G);
	return 0;
}

Time complexity O(v2)

Note: the main test is manual calculation. If there is a negative weight in the path, this algorithm is not suitable.

3.2.2 shortest path between vertices:

Floyd algorithm (weighted graph, non weighted graph)

Floyd algorithm (Floyd warhall algorithm)
Heap sorting algorithm

for*3 algorithm:

Using the idea of dynamic programming, the solution of the problem is divided into several stages
For a graph G with n vertices, finding the shortest path between any pair of vertices VI - > VJ can be divided into the following stages: # initial: transit at other vertices is not allowed. What is the shortest path?
0: if transfer in V0 is allowed, what is the shortest path?
1: If transfer is allowed in V0 and V1, what is the shortest path?
2: If transfer is allowed in V0, V1 and V2, what is the shortest path?
...
n-1: if transfer is allowed in V0, V1, V2... Vn-1, what is the shortest path?

Auxiliary matrix:
A(i): at present, the shortest path length between vertices
path(i): the transition point between two vertices

That is, if a (k-1) [i] [J] > A (k-1) [i] [k] + a (k-1) [k] [J]
Then A(k)[i][j] = A(k-1)[i][k] + A(k-1)[k][j], path(k)[i][j] = k
Otherwise, A(k) and path(k) remain the original values.

Initialization: A(-1): it is the adjacency matrix of the graph without passing through any point; path(-1): the transfer point between two vertices, all of which are - 1;

A	V0	V1	V2		path	V0	V1	V2
V0	0	6	13		V0	-1	-1	-1
V1	10	0	4		V1	-1	-1	-1
V2	5	∞	0		V2	-1	-1	-1

After three rounds, the corner mark I indicates the position of the i-th round change

A	V0	V1	V2		path	V0	V1	V2
V0	0	6	102		V0	-1	-1	1
V1	93	0	4		V1	2	-1	-1
V2	5	111	0		V2	-1	0	-1

//... preparation, initialize matrix A and path according to the information in the figure (as shown in the figure above)
for (int k=0; k<n; k++){					//Consider vk as the transit point
	for (int i=0; i<n; i++){				//Traverse the whole matrix, i is the row number and j is the column number
    	for (int j=0; j<n; j++){
			if (A[i][j]>A[i][k]+A[k][j]){	//The path with vk as the transit point is shorter
                A[i][j]=A[i][k]+A[k][j];	//Update shortest path length
				path[i][j]=k;				//Transit point
			}}}}
void find(int x, int y)							//Output path
{
	if (path[x][y] == -1) {						//If there is no node between X and y, the lookup ends
		return;
	}
	else {										//If there is a node T between X and y, find t, y
		int t = path[x][y];
		find(t, y);			
		cout << "->" << t;
	}
	return;
}

void wayoutput(MGraph &G, int p)
{
	for (int i = 0; i < G.vex; i++)			
		{
			cout << "from v"<< p <<" reach v" << i << "The shortest path length is:" << A[p][i] << endl;
			cout << "Path is: "<<p;
			find(p, i);
			cout << "->" << i << endl;
		}
}

Time complexity O(v3)

Note: the main test is manual calculation. If there are negative weights in the path, this algorithm is also suitable, but if the graph contains a loop with negative weights, it is not suitable.

summary	BFS algorithm	Dijkstra algorithm	Floyd algorithm
have no right	✔	✔	✔
With right	✘	✔	✔
With negative weight	✘	✘	✔
Circuit with negative weight	✘	✘	✘
Time complexity	O(|V|2) or O(|V|+|E|)	O(|V|2)	O(|V|3)
Usually used for	Find the shortest path of the cell of the weight graph	Finding the shortest path of a weighted graph	Find the shortest path between vertices in weighted graph

3.3 directed acyclic graph

Directed acyclic graph: if there is no ring in a directed graph, it is called directed acyclic graph (DAG graph)

3.3.1 description expression

Find the minimum number of nodes required to describe the expression with a directed acyclic graph
i. Arrange the operands in a row without repetition
ii. Mark the effective order of each operator (it doesn't matter if the order is a little different)
iii. add operators in order and pay attention to "layering"
iv. check whether operators in the same layer can be merged from bottom to top

Example: (a * b) * (a * b) * (a * b) * c

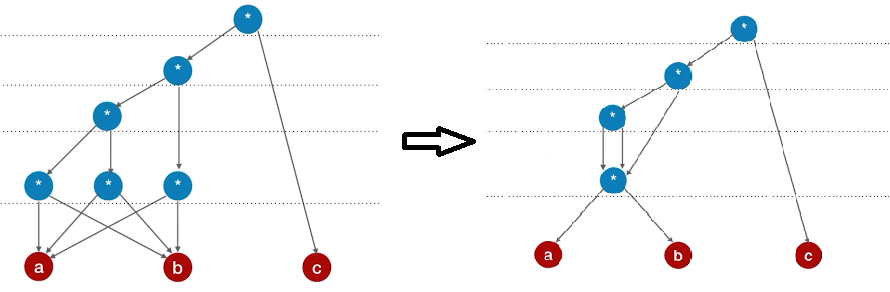
Note: each operand can occur at most once

3.3.2 topology sorting

AOV network (Activity on vertex Network):
A DAG graph (directed acyclic graph) is used to represent a project. The vertex represents the activity, and the directed edge < Vi, Vj > represents the activity. Vi must precede the activity Vj

Topological sorting: find the order of doing things

Definition 1: in graph theory, a sequence of vertices of a directed acyclic graph is called a topological ordering of the graph if and only if the following conditions are met:
① Each vertex appears only once.
② If vertex 4 is ahead of vertex B in the sequence, there is no path from vertex B to vertex A in the graph.

Definition 2: topological sorting is A sorting of the vertices of A directed acyclic graph. It makes vertex B appear after vertex A in the sorting if there is A path from vertex A to vertex B. Each AOV network has one or more topological sorting sequences.

Implementation of topology sorting (must be a directed acyclic graph):
i. Select a vertex without precursor from AOV network and output it.
ii. Delete the vertex and all directed edges starting from it from the net.
iii. repeat i and ii until the current AOV network is empty or there is no Vertex without precursor in the current network.

#define MaxvertexNum 100 		// The maximum number of vertices in a graph
typeder struct ArcNode{			//Edge table node
	int adjvex;					//The position of the vertex to which the arc points
	struct Arcode *nextarc;		//Pointer to the next arc 
    //InfoType info; 			// Edge weights of nets
}ArcNode;
typedef struct vNode{			//Vertex table node
	vertexType data;			//Vertex information
	ArcNode *firstarc;			//Pointer to the first arc attached to the vertex
}VNode, AdjList[MaxvertexNum];
typedef struct{
	AdjList vertices;			//Adjacency table
	int vexnum, arcnum;			//The number of vertices and arcs of a graph
}Graph;							//Graph is a graph type stored as an adjacency table
int indefree[MaxvertexNum]		//The penetration of the current vertex
int print[MaxvertexNum]			//Record topology sort sequence
bool Topologicalsort ( Graph G){
    InitStack(S);				//Initialize the stack and store vertices with a degree of 0
	for(int i=0 ; i<G.vexnum;i++)
		if (indegree[i]==0 )
			Push (S,i);			//Stack all vertices with degree 0
		int count=0;			//Count to record the number of vertices that have been output
		while(!IsEmpty(s) ){	//If the stack is not empty, there are vertices with a degree of 0
            Pop(S,i);			//Stack top element out of stack
			print[count++]=i;	//Output vertex i
		for( p=c.vertices [ i].firstarc;p;p=P->nextarc ) {
		//Reduce the in degree of all vertices pointed to by i by 1, and press the vertices whose in degree is reduced to o into stack S
            v=p->adjvex;
            indegree[v] = indegree[v] - 1;
			if(indegree[v] == 0)
				Push (S,v);		//If the entry degree is 0, it will be stacked
        }//rof
	}//elihw
	if (count<G.vexnum)
        return false;			//Sorting failed, there is a loop in the directed graph
	else
        return true;			//Topology sorting succeeded

Similarly, inverse topological sorting can be realized. At this time, it is convenient to use adjacency matrix or inverse adjacency table to store graphs.

void DFSTraverse(Graph G){		//Depth first traversal of figure G
	for(v=0; v<G.vexnum; ++v)
		visited[v]=FALSE;		//Initialize accessed tag data
	for(v=0; v<G.vexnum; ++v)	//This code starts from v=0
		if(!visited[v])
			DFS(G,v);
}
void DFS(Graph G,int v){		//Starting from vertex v, depth first traverses graph G
	visit(v);					//Access vertex v
	visited[v]=TRUE;			//Set accessed flag
	for(w=FirstNeighbor(G,v ); w>=0; w=NextNeighor(G,v,w)){
		if(!visited [w]){		//Adjacent vertices not yet accessed with w as u
			DFS(G,w);
		}//fi
    }//rof
    print(v);					//Output vertex
}

3.3.3 critical path

In a weighted directed graph, an event is represented by a vertex, an activity is represented by a directed edge, and the cost of completing the activity (such as the time required to complete the activity) is represented by the weight on the edge. It is called an activity on edge network (AOE network for short)

AOE network has the following properties:
i. Only after the event represented by a vertex occurs, the activities represented by each directional edge starting from the vertex can start;
ii. The event represented by a vertex can occur only when the activities represented by each directed edge entering a vertex have ended. In addition, some activities can be carried out in parallel;
iii. in the AOE network, there is only one vertex with in degree O, called the start vertex (source point), which represents the beginning of the whole project; there is also only one vertex with out degree 0, called the end vertex (sink point), which represents the end of the whole project.

There may be multiple directed paths from the source point to the sink point. Among all paths, the path with the maximum path length is called critical path, and the activities on the critical path are called critical activities.

Earliest start time e(i) of activity a: refers to the earliest occurrence time of the event represented by the starting point of the active arc
Latest start time l(i) of activity a: it refers to the difference between the latest occurrence time of the event represented by the end of the activity arc and the time required for the activity.
Time margin iHN)-e(i) of activity a: represents the time that activity a can delay without increasing the total time required to complete the whole project.
If the time margin of an activity is zero, it means that the activity must be completed on schedule. Activity a with d(i)=0, i.e. l(i)=e(i) is a key activity, and the path composed of key activities is a key path

Steps:
i. Find the earliest occurrence time (VE) of all events and the fastest end time of the activity before the current activity
Find the ve() of each vertex according to the topological sorting sequence:
Ve (source point) = 0; ve(k) = Max{ve(j) + Weight(Vj, Vk)} Vj is any precursor of Vk

ii. Find the latest occurrence time vl() of all events and the latest start time of the current activity
Sort the sequence according to the inverse topology, and find the vl() of each vertex in turn:
VL (sink) = ve (sink); vl(k) = Min{vl(j) - Weight(Vk, Vj)} Vj is any successor of Vk

iii. find the earliest occurrence time e() of all activities and the earliest start time of the starting event of the active arc
If edge < VK, VJ > represents active ai, then e(i)=ve(k)

iv. calculate the latest occurrence time I() of all activities, and the difference between the latest occurrence time of the end point of the activity arc and the time required for the activity
If edge < VK, VJ > indicates active ai, then l(i)=vl(j) - Weight(Vk, Vj)

v. Find the time margin of all activities. Activities with D () = 0 are key activities (edges)
The vertices corresponding to the activity of d(i) = l(i) - e(i), d(i) = 0 form a path

If the time of key activities increases, the construction period of the whole project will increase; shortening the time of key activities can shorten the construction period of the whole project;
When shortened to a certain extent, key activities may become non key activities;
There may be multiple critical paths. Only increasing the speed of key activities on one critical path can not shorten the construction period of the whole project. Only accelerating those key activities included in all critical paths can achieve the purpose of shortening the construction period.