Data structure - minimum spanning tree QuickPass Guide

1. Introduction to spanning tree and minimum spanning tree

An important difference between a tree and a graph is that there is no loop in the tree, and a spanning tree is to remove the loop by removing some edges from the part that constitutes the loop in the graph. The resulting tree is called a spanning tree. When each edge has weights, the tree with the smallest sum of total weights is called the minimum spanning tree, and the algorithm for finding the minimum spanning tree mainly uses two minimum spanning tree algorithms.

2. Minimum spanning tree algorithm I: Kruskal algorithm (Kruskal algorithm)

Kruskal is an edge adding algorithm. Its idea is to sort all edges in ascending order according to their weights, add the edges to the point graph in turn, and judge whether a loop is formed. If a loop is formed, it will not be added, and if not, it will be added until the edges are added or the minimum spanning tree is constructed. It is more suitable for graphs with sparse edges.

It involves the knowledge of judging the loop and searching the set. If you don't know, you can take a look at it first: Data structure - parallel search set speed Guide

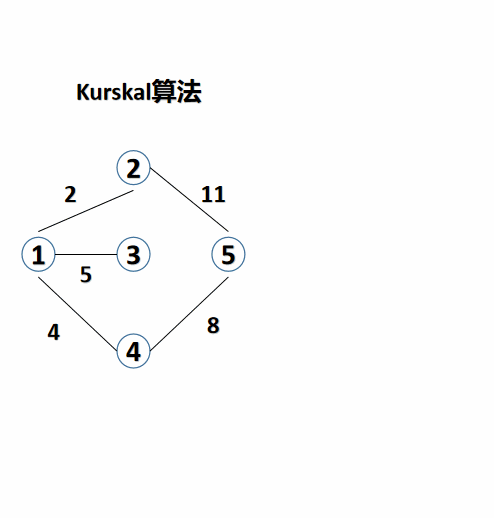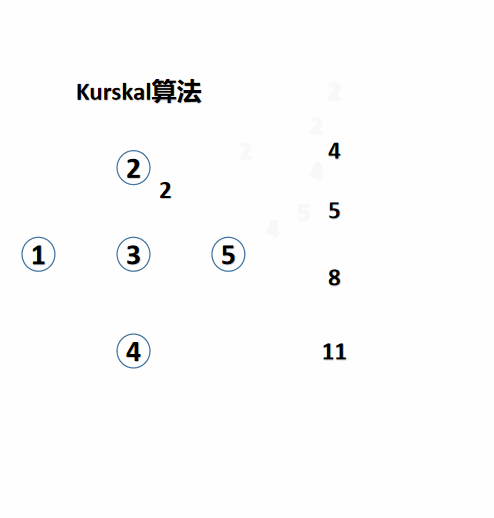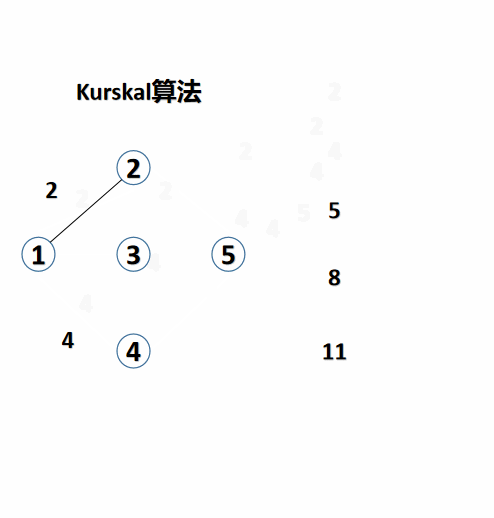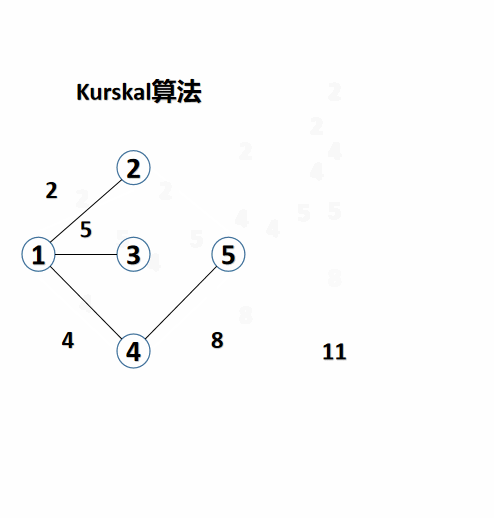
K r u s k a l : { 1. yes edge Press power Row order 2. Press power value from Small reach large plus edge ， plus Yes after yes no structure become return ring ？ { 1. structure become ， no plus edge 2. no structure become ， plus edge 3. edge no enough or person most Small living become tree finish become ， junction beam Kruskal: \begin{cases} 1. Sort edges by weight \ \ 2. Add edges from small to large according to weight. Does it form a loop\ begin{cases} 1. Form, without edges \ \ 2. Do not form, with edges \ \ end{cases}\ 3. The edges are not enough or the minimum spanning tree is completed. end{cases} Kruskal: ⎩⎪⎪⎨⎪⎪⎧ 1. The opposite edges are sorted by weight. 2. The edges are added from small to large according to the weight. Does the addition form a loop? {1. Composition, no edges 2. No composition, edges 3. Not enough edges or the minimum spanning tree is completed, end

#include<bits/stdc++.h>
using namespace std;

vector<pair<int,pair<int,int> > > edge;
int pre[MAXN];
int weight;

int find(int x){//Combined search
    if(pre[x] == x) return x;
    else return find(pre[x]);
}

void join(int x,int y){//Merge search set merge
    x = find(x),y = find(y);
    if(x != y) pre[x] = y;
}

int main(){
    for(int i = 0;i < MAXN;i++) pre[i] = i;//Initialization of the subsequence array before merging
    
    sort(edge.begin(),edge.end(),[](pair<int,pair<int,int> > 						a,pair<int,pair<int,int> > b){return a.second.second < b.second.second});//Sort edges
    
    int num = 0;//Record the number of edges added
    for(int i = 0;i < edge.size();i++){
		if(find(edge[i].first) != find(edge[i].second.first){//If the root node is different, it indicates 		  // If no loop is formed, the edge is added
             join(edge[i].first,edge[i].second.first);
             num++;//Add the number of sides plus one
             weight += edge[j].second.second;//Minimum weight accumulation
        }
        if(num >= pointnum - 1) break;//When the number of added edges is the number of points minus one, it indicates that the minimum spanning tree has been generated 		 End cycle
    }
           
    if(num >= pointnum - 1) cout << weight;//Judge whether the minimum spanning tree is generated successfully. If it is successful, the minimum spanning tree will be output 	  // Weight 
    else cout << -1;//Output - 1 if failed
           
    return 0;
}

3. Minimum spanning tree algorithm II: Prim algorithm (Prim algorithm)

Prim algorithm is as like as two peas, which is based on blue white point. So its code is highly similar to that of Dijkstra algorithm, which is the same as the blue white point algorithm. , the shortest path algorithm first digs a hole, then fills it in, and then adds a hyperlink here. Its idea is to select a point, then find the edge with the smallest weight around, mark its point, and repeat the steps from that point next time. It is more suitable for graphs with dense edges.

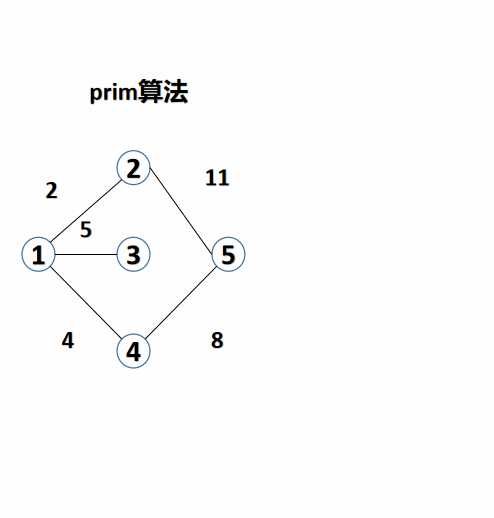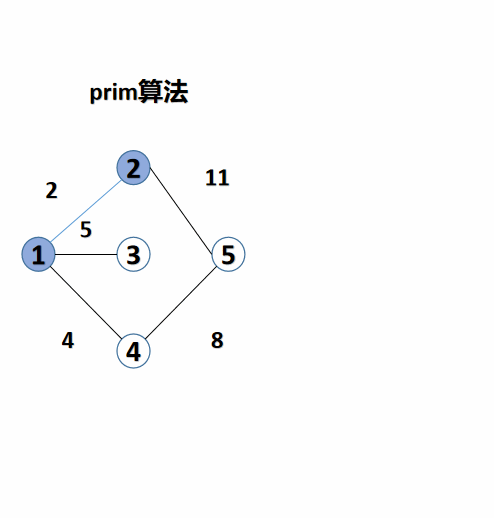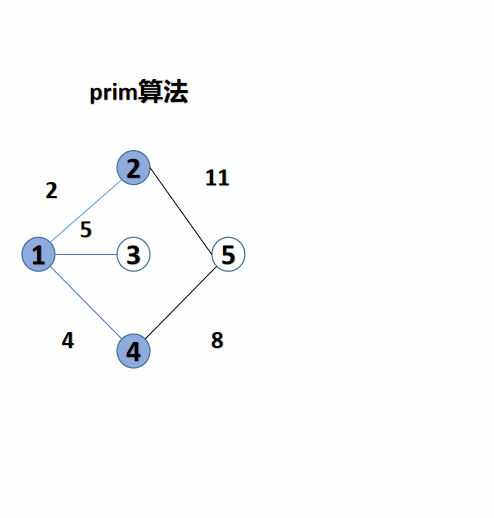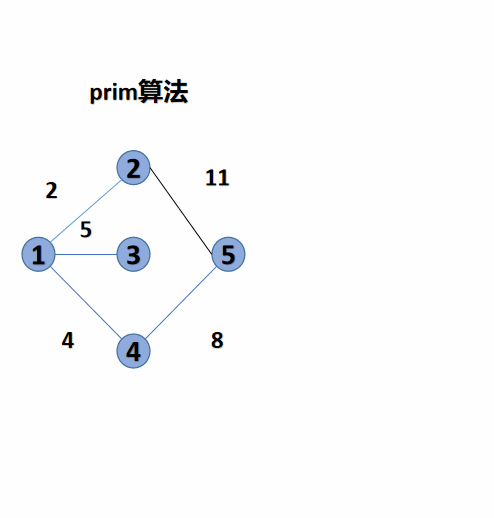
#include<bits/stdc++.h>
using namespace std;
const long long INF = 0x3f3f3f3f;
int mp[MAXN][MAXN];
bool book[MAXN];
int mindist[MAXN];
int sum;

int main(){
    //initialization
    for(int i = 0;i < MAXN;i++) mindist[i] = INF;
    mindist[1] = 0;
    book[1] = true;
    int num = 0;
    
    while(num++ < pointnum - 1){
        int m = INF,k = 0;
        for(int i = 1;i < MAXN;i++){//Find the shortest distance point
            if(mindist[i] < m){
                m = mindist[i];
                k = i;
            }
	    }
        sum += mindist[k];//Minimum weight accumulation
        book[k] = true;//sign
        for(int i = 1;i < MAXN;i++){//Update mindist
			if(!book[i] && mp[k][i] < mindist[i]){
                mindist[i] = mp[k][i];
            }
        }
    }
    
    for(int i = 1;i < MAXN;i++) if(mindist[i] == INF) cout << -1,return 0;//Failed output - 1
    cout << sum;//Successful output of minimum weight
    return 0;
}

4. Minimum spanning tree related exercises

Do one by one~