Even if there is no talent, as long as you are willing to spend a little time every day, do the same thing, unconsciously, you will go far.
What is a linear table?
A linear table is a finite sequence of n (n > = 0) elements. In the table, there is a linear logical relationship between elements: (1) There is only one start node in the table; (2) There is only one terminal node; (3) Except for the start node, each node in the table has only one predecessor node; (4) Except terminal nodes, each node in the table has only one successor node; According to their relationship, they can be arranged into an existing linear sequence, which is recorded as: (a1, a2,..., an) For example, 26 English alphabets (A,B,C,...,X,Y,Z) are a linear table ai (1 < = I < = n) here belongs to the same data object and has the same data type. Data elements in linear tables The number n is the length of the linear table, which is called table length. When n=0, it is an empty table. i is the bit order of data element ai.
How to store linear tables
Linear tables can be stored in two ways: sequential storage and chained storage
(1) Sequence table
Sequential storage is to store the data elements of linear table in sequence with a piece of memory with continuous address. The sex table with sequential storage structure is called sequential table, and the logically adjacent data elements in the sequential table are also adjacent in the physical storage location. As long as the starting position of the linear table is determined, any data in the linear table can be accessed randomly: The address of the ith element is: Loc(ai) = Loc(a1) + size * (i - 1) where size is the space occupied by each element.
Implementation of C language version
#include <stdio.h>
#include <stdlib.h>
#define ERROR 0
#define OK 1
#define TRUE 1
#define FALSE 0
#define NOTFOUND -1
#define MAXSIZE 100
#define seqNodeDataType int
//Definition of structure
typedef struct seqNode{
seqNodeDataType data[MAXSIZE];
int length;
}SeqNode;
//Initialization
void Init_SeqList(SeqNode * L){
L->length = 0;
}
//Sentence blank
int IsEmpty_SeqList(SeqNode L){
if (L.length == 0) {
return TRUE;
} else {
return FALSE;
}
}
//Sentence full
int IsFull_SeqList(SeqNode L){
if (L.length == MAXSIZE - 1) {
return TRUE;
} else {
return FALSE;
}
}
//Get real length
int GetListLength_SeqList(SeqNode L){
return L.length;
}
//Get the element at index
seqNodeDataType GetElem_SeqList(SeqNode L, int index){
if (index < 0 || index >= L.length) {
return ERROR;
}
return L.data[index];
}
//Search by value
int IndexOf_SeqList(SeqNode L, seqNodeDataType elem){
for (int i = 0; i < L.length; ++i) {
if (L.data[i] == elem) {
return i;
}
}
return NOTFOUND;
}
//Printout
void Print_SeqList(SeqNode L){
printf("[");
for (int i = 0; i < L.length; ++i) {
if (i == L.length - 1) {
printf("%d", L.data[i]);
} else {
printf("%d,", L.data[i]);
}
}
printf("]\n");
}
//Insert element at index
int InsertOfIndex_SeqList(SeqNode *L, int index, seqNodeDataType elem){
if (index < 0 || index > L->length) {
return ERROR;
}
if (IsFull_SeqList(*L)) {
return ERROR;
}
for (int i = L->length; i > index; --i) {
L->data[i] = L->data[i - 1];
}
L->data[index] = elem;
L->length++;
return OK;
}
//Add element at the beginning
int InsertFirst_SeqList(SeqNode *L, seqNodeDataType elem){
InsertOfIndex_SeqList(L, 0, elem);
}
//Tail add element
int InsertLast_SeqList(SeqNode *L, seqNodeDataType elem){
InsertOfIndex_SeqList(L, L->length, elem);
}
//Delete elements
int DeleteOfIndex_SeqList(SeqNode *L, int index, seqNodeDataType *result){
if (index < 0 || index > L->length) {
return ERROR;
}
if (IsEmpty_SeqList(*L)) {
return ERROR;
}
for (int i = index; i < L->length - 1; ++i) {
L->data[i] = L->data[i + 1];
}
L->length--;
return OK;
}
//wipe data
int Clear_SeqList(SeqNode *L){
L->length = 0;
return OK;
}
What are the disadvantages
Because the underlying implementation of the sequence table is an array, and the capacity of the array cannot be changed, the biggest problem is how much space allocation is appropriate? Too small data can not continue to store, and too large space waste. High level language can be used to optimize the sequence table and realize dynamic array expansion.
Java implementation
package cn.boom.list;
public class SeqList<T> {
private T[] data;
private int size;
//Non parametric structure
public SeqList(){
data = (T[]) new Object[10];
size = 0;
}
//Structures with parameters: parameter capacity
public SeqList(int capacity) {
data = (T[]) new Object[capacity];
size = 0;
}
/**
* Get the real length (number of data)
* @return size
*/
public int getSize(){
return this.size;
}
/**
* Get elements of index location
* @param index
* @return data[index]
* @throws IllegalArgumentException Illegal parameter exception
*/
public T getIndexOf(int index) throws IllegalArgumentException{
//Parameter validity verification
if (index < 0 || index >= size) {
throw new IllegalArgumentException("Illegal Index !");
}
return this.data[index];
}
//Modified value
public void set(int index, T elem) {
if (index < 0 || index >= size) {
throw new IllegalArgumentException("Illegal Index !");
}
data[index] = elem;
}
/**
* Search by value return elem first occurrence subscript not found return - 1
* @param elem
* @return index
*/
public int locationElem(T elem){
for (int i = 0; i < this.size; i++) {
if (elem.equals(this.data[i])) {
return i;
}
}
return -1;
}
//Element present or not
public boolean contains(T elem){
return locationElem(elem) != -1;
}
//Whether the table is empty
public boolean isEmpty(){
return (size == 0);
}
//Whether the table is empty
public boolean isFull(){
return (size == data.length);
}
//Capacity acquisition
public int getCapacity(){
return data.length;
}
//Insert an element at index
public void add(int index, T elem) {
//Parameter validity verification
if (index < 0 || index > size) {
throw new IllegalArgumentException("Illegal Index ! index is " + index);
}
if (isFull()) {
updateCapacity(data.length * 2);
}
//Data move backward after index
for (int i = size; i > index; i--) {
this.data[i] = this.data[i - 1];
}
this.data[index] = elem;
size++;
}
//Add element at the beginning of array
public void addFirst(T elem) {
add(0, elem);
}
//Add elements at the end of the array
public void addLast( T elem){
add(this.size,elem);
}
//Update array capacity
public void updateCapacity(int newCapacity) {
T[] newArray = (T[]) new Object[newCapacity];
for (int i = 0; i < size; i++) { // copy the data in the original array
newArray[i] = data[i];
}
this.data = newArray;
}
//Delete the element with index as its subscript and return
public T remove(int index){
if (index < 0 || index > size) {
throw new IllegalArgumentException("Illegal Index ! index is " + index);
}
T elem = data[index];
for (int i = index; i < size - 1; i++) {
data[i] = data[i + 1];
}
size--;
if (size < data.length / 2) { //Shrinkage capacity
updateCapacity(data.length / 2);
}
return elem;
}
//Delete first element
public T removeFirst() {
return remove(0);
}
//Delete last element
public T removeLast() {
return remove(size - 1);
}
@Override
public String toString() {
StringBuilder res = new StringBuilder();
res.append("SeqList{");
res.append(" data=[");
for (int i = 0; i < this.size; i++) {
res.append(this.data[i].toString());
if (i != size - 1) {
res.append(',');
}
}
res.append("], size=" + size + ", capacity=" + getCapacity() + " }");
return res.toString();
}
}
Although the above code realizes the dynamic expansion and reduction of array space, the sequence table is still a non dynamic storage structure. The following describes the list of dynamic storage structures.
(2) Single chain table
Linked list is a set of arbitrary storage units to store data elements in a linear table. This set of storage units can be continuous or discontinuous. In order to establish a linear relationship between data elements, for each data element an, in addition to storing its own information, it must also contain information indicating the storage location of the direct successor elements of the element, These two parts of information form a "node", that is, each node includes at least two domains, one domain stores data element information, which is called data domain; the other domain stores the address of the direct successor element, which is called pointer domain.

Sometimes for the convenience of operation, a node is added before the first node of a single chain table, which is called the head node. The data field of the head node can store information such as title, table length, etc., or it can not store any information. Its pointer field stores the first address of the first node, and the head node points from the head pointer.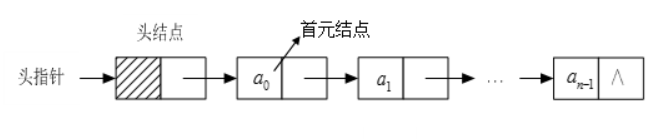
Single chain table C
#include <stdio.h>
#include <stdlib.h>
#define ERROR 0
#define OK 1
#define TRUE 1
#define FALSE 0
#define NOTFOUND -1
#define linkedListDataType int
typedef struct linkedNode{
linkedListDataType data;
struct linkedNode* next;
}LNode;
//Establishing single chain table by head insertion
int CreateHead_LinkedList(LNode ** H){
(*H)->next = NULL;
int elem;
scanf("%d",&elem);
while (elem != -1) {
LNode* s = (LNode *) malloc(sizeof(LNode));
s->data = elem;
s->next = (*H)->next;
(*H)->next = s;
scanf("%d", &elem);
}
return OK;
}
//Initialize linked list
LNode *Init_LinkedList() {
LNode *H = (LNode *) malloc(sizeof(LNode));
if (H == NULL) {
return ERROR;
}
H->next = NULL;
return H;
}
//Establishing single chain table by tail insertion
int CreateTail_LinkedList(LNode ** H){
(*H)->next = NULL;
LNode *p = *H;
int elem;
scanf("%d",&elem);
while (elem != -1) {
LNode* s = (LNode *) malloc(sizeof(LNode));
s->data = elem;
s->next = NULL;
p->next = s;
p = s;
scanf("%d", &elem);
}
}
//Get link length
int GetSize_LinkedList(LNode *H){
LNode *p = H;
int size = 0;
while (p->next != NULL) {
size++;
p = p->next;
}
return size;
}
//Judge whether the list is empty
int IsEmpty(LNode *H){
if ( H == NULL || GetSize_LinkedList(H) == 0) {
return 1;
}
return 0;
}
//Output print list
void Print_LinkedList(LNode *H){
LNode *p = H;
printf("head -> ");
while (p->next != NULL) {
printf("%d -> ", p->next->data);
p = p->next;
}
printf("NULL\n");
}
//Get index node
LNode* GetNode_LinkedList(LNode *H, int index) {
if (index == -1) {
return H;
}
LNode *p = H;
int count = 0;
while (p->next != NULL) {
p = p->next;
if (index == count) {
return p;
}
count++;
}
return NULL;
}
//Delete nodes by index
int DeleteNodeByIndex_LinkedList(LNode *H, int index) {
LNode *p = GetNode_LinkedList(H, index - 1);
LNode *q = p->next;
p->next = p->next->next;
free(q);
return OK;
}
//Insert a node at the index
int InsertNodeIndexOf_LinkedList(LNode *H, int index, linkedListDataType elem) {
if (index > GetSize_LinkedList(H)) {
return ERROR;
}
LNode *p = GetNode_LinkedList(H, index - 1);
LNode* s = (LNode *) malloc(sizeof(LNode));
if (s == NULL) {
return ERROR;
}
s->data = elem;
s->next = p->next;
p->next = s;
return OK;
}
//Insert an element at the end of the list
int InsertNodeTail_LinkedList(LNode *H, linkedListDataType elem) {
InsertNodeIndexOf_LinkedList(H,GetSize_LinkedList(H),elem);
return OK;
}
//Modify the value of the node at the index
int UpdateNodeByIndex_LinkedList(LNode *H, int index, linkedListDataType elem){
LNode *p = GetNode_LinkedList(H, index);
p->data = elem;
return OK;
}
//Delete duplicate element node
void DeleteRepeatElem(LNode *H){
if (H == NULL) {
return;
}
LNode *p = H->next;
if (p == NULL) {
return;
}
while (p->next != NULL) {
LNode *q = p->next;
while (q != NULL) {
if (p->data == q->data) {
//Delete q node
LNode *t = q;
q = q->next;
free(t);
p->next = q;
} else {
q = q->next;
}
}
p = p->next;
}
}
Java implementation of single chain table
package cn.boom.list;
public class LinkedList<T> {
private Node head;//Virtual head node
private int size;//Table length
private class Node {
private T data;
private Node next;
public Node() {
this.data = null;
this.next = null;
}
public Node(T data) {
this.data = data;
this.next = null;
}
public Node(T data, Node node) {
this.data = data;
this.next = node;
}
}
public LinkedList() {
this.head = new Node();
this.size = 0;
}
/**
* Get link length
* @return
*/
public int getSize() {
return this.size;
}
/**
* Judge whether the list is empty
* @return
*/
public boolean isEmpty() {
return size == 0;
}
/**
* Add a new element in the index(0-size) position of the linked list
* @param index
* @param elem
*/
public void add(int index, T elem) {
if (index < 0 || index > size) {
throw new IllegalArgumentException("Index Is Illegal Argument ! index = " + index);
}
Node node = this.head;
for (int i = 0; i < index ; i++) { //Find the previous node to insert the subscript
node = node.next;
}
Node e = new Node(elem);
//Insert Knot
e.next = node.next;
node.next = e;
this.size++;
}
/**
* Add new elements at the head of the list
* @param elem
*/
public void addFirst(T elem) {
add(0,elem);
}
/**
* Add new elements at the end of the list
* @param elem
*/
public void addLast(T elem) {
add(size,elem);
}
/**
* Get the element at the index(0-size) position of the linked list
* @param index
* @return
*/
public T get(int index) {
if (index < 0 || index >= size) {
throw new IllegalArgumentException("Index Is Illegal Argument ! index = " + index);
}
Node node = this.head.next;
for (int i = 0; i < index; i++) {
node = node.next;
}
return node.data;
}
/**
* Modify the element at the index(0-size) position of the linked list
* @param index
* @param elem
*/
public void set(int index, T elem) {
if (index < 0 || index >= size) {
throw new IllegalArgumentException("Index Is Illegal Argument ! index = " + index);
}
Node node = this.head.next;
for (int i = 0; i < index; i++) {
node = node.next;
}
node.data = elem;
}
/**
* Query whether the element is included in the table
* @param elem
* @return
*/
public boolean contains(T elem) {
Node node = this.head.next;
while (node != null) {
if (node.data.equals(elem)) {
return true;
}
node = node.next;
}
return false;
}
/**
* Delete the node at index(0-size) and return data
* @param index
* @return
*/
public T remove(int index) {
if (index < 0 || index >= size) {
throw new IllegalArgumentException("Index Is Illegal Argument ! index = " + index);
}
Node node = this.head.next;
for (int i = 0; i < index - 1; i++) { //Find the previous node to delete
node = node.next;
}
Node s = node.next;
node.next = s.next;
s.next = null;
this.size--;
return s.data;
}
/**
* Remove element e from table
* @param elem
*/
public void removeElement(T elem) {
Node preNode = this.head;
Node node = preNode.next;
while (node != null) {
if (node.data.equals(elem)) {
preNode.next = node.next;
node.next = null;
node = preNode.next;
this.size--;
continue;
}
preNode = node;
node = node.next;
}
}
@Override
public String toString() {
Node node = this.head.next;
StringBuilder res = new StringBuilder();
res.append("head -> ");
for (int i = 0; i < this.size; i++) {
res.append(node.data.toString() + " -> ");
node = node.next;
}
res.append("NULL");
return res.toString();
}
}
Advantages and disadvantages of sequence list and chain list
Advantages of sequence table: (1) Using array to store data elements is simple and easy to implement. (2) No additional storage overhead is needed to represent the logical relationship between nodes. (3) High storage density. (4) Sequence table can access nodes randomly according to element bit order. Disadvantages: (1) When doing insert and delete operations, a large number of data elements must be moved, which is inefficient. (2) To occupy continuous storage space, storage allocation can only be done in advance. If the estimation is too large, it may lead to a large number of empty rear; if the pre allocation is too small, it will cause data overflow. The advantages and disadvantages of linked list are just opposite to the sequence list.
Reference
[1] Wang Shuyan. Data structure and algorithm: People's post and Telecommunications Press

