data structure

Basic concept and operation of linear table (I)

Mind map

2.1 definition and basic operation of linear table

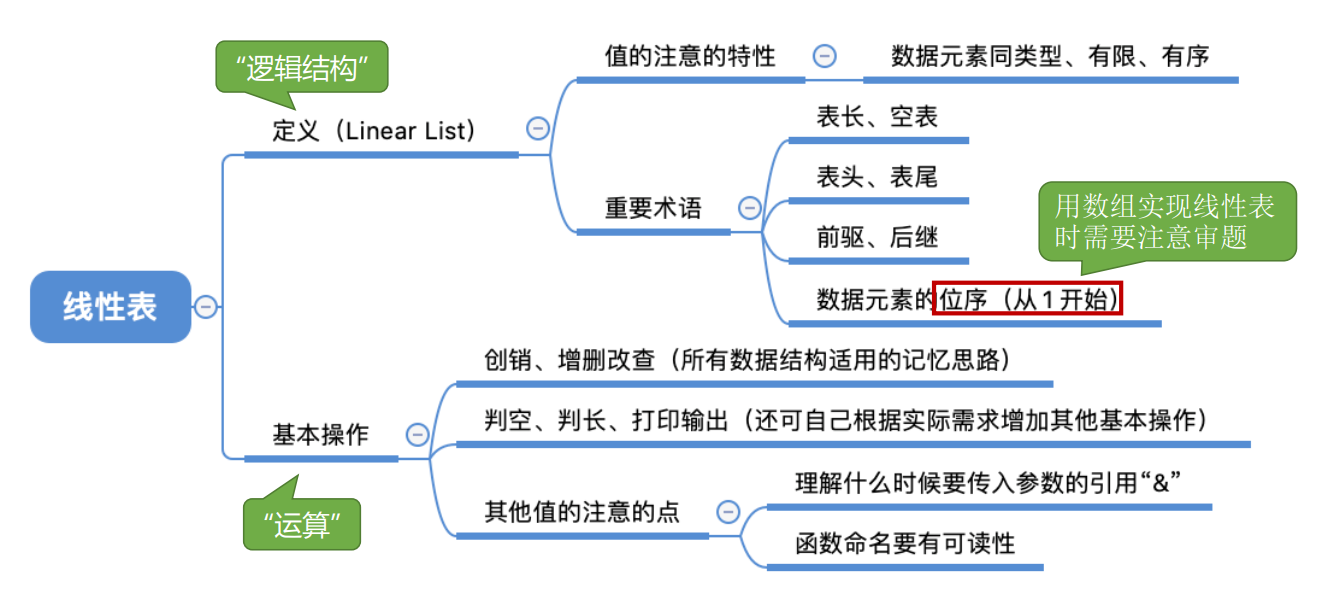
2.1.1 definitions

A linear table is a finite sequence of n (n ≥ 0) data elements with the same data type, where n is the table length. When n = 0, the linear table is an empty table. If L is used to name the linear table, it is generally expressed as

L = ( a 1 , a 2 , ... , a i , a i + 1 , ... , a n ) L = (a_1, a_2, ... , a_i, a_i+1, ... , a_n) L=(a1​,a2​,...,ai​,ai​+1,...,an​)

Several concepts:
a i a_i ai ， is the "ith" element in the linear table and the bit order in the linear table
a 1 a_1 a1 is the header element; a n a_n an is the footer element.
Except for the first element, each element has and has only one direct precursor; Except for the last element, each element has and has only one direct successor.

2.1.2 basic operation

Initlist: initialize table. Construct an empty linear table L and allocate memory space.

Destroylist: destroy operation. Destroy the linear table and free the memory space occupied by linear table L.

Listinsert (& L, i, e): insert operation. Insert the specified element E at position i in table L.

ListDelete & L, i, & e: delete operation. Delete the element at position i in Table L and return the value of the deleted element with e.

Locaterelem (L, e): find operation by value. Finds an element with a given keyword value in table L.

GetElem(L,i): bitwise lookup operation. Gets the value of the element at position i in table L.

Other common operations:

Length(L) find the table length. Returns the length of linear table L, that is, the number of data elements in L.

PrintList(L) output operation. Output all element values of linear table L in sequence.

Empty(L) empty judgment. If l is an empty table, it returns true; otherwise, it returns false.

2.2 sequential representation of linear table

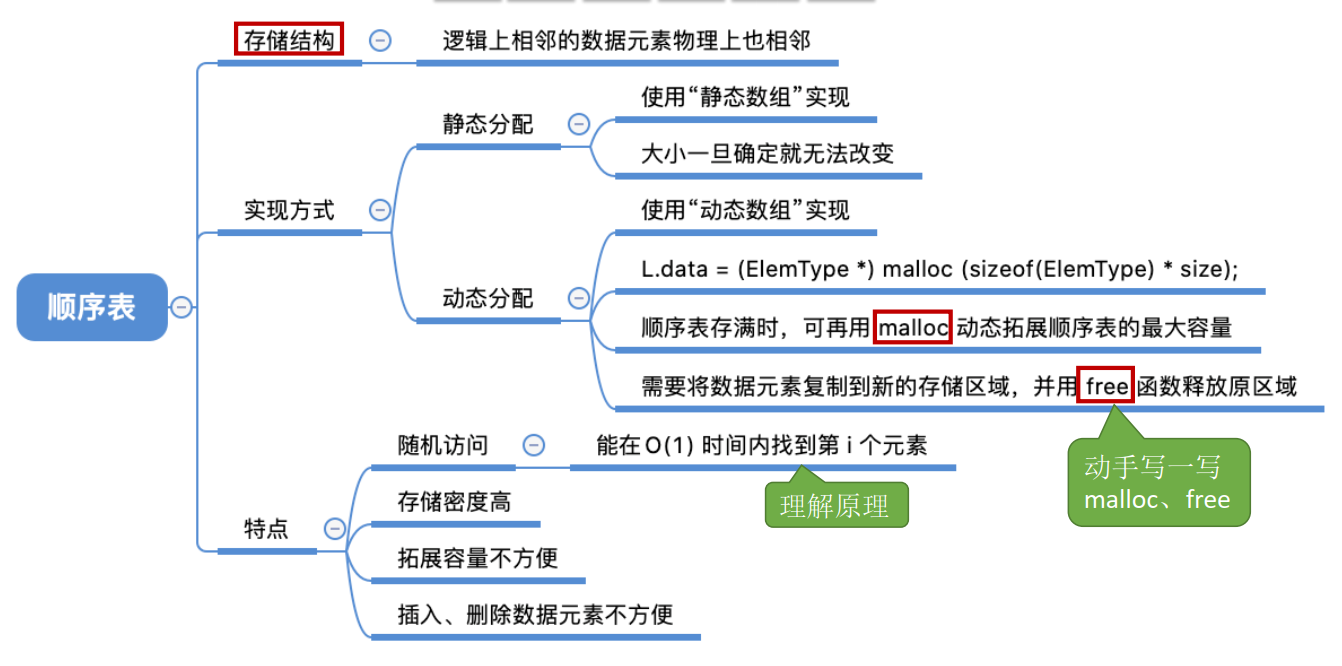
2.2.1 definitions

Definition: sequential table – realize the sequential storage of linear table by sequential storage. Logically adjacent elements are stored in storage units that are also adjacent in physical locations, and the relationship between elements is reflected by the adjacency relationship of storage units.

1. Static allocation

Allocate continuous storage space for each data element, with the size of MaxSize * sizeof(ElemType)

#include <stdio.h>
#define MaxSize 10 / / define the maximum length
typedef struct SqList
{
    /* data */
    int data[MaxSize]; //Use a static "array" to store data elements
    int length;        //Current length of sequence table
};

void InitList(SqList &L)
{
    L.length = 0; //The initial length of the sequence table is 0;
}

int main()
{
    SqList L; //Declare a sequence table
    InitList(L); //initialization
    for (int i = 0; i < L.length; i++)
    {
        /* code */
        printf("data[%d]=%d\n", i, L.data[i]);
    }
    return 0;
}

2. Dynamic allocation

C language knowledge

1. Malloc is a system function, which is the abbreviation of memory allocate. Where memory means "memory" and allocate means "allocate". As the name suggests, malloc functions

Allocate memory. To call it, you must include the header file < stdlib. H >.

The return value of malloc function is an address, which is the starting address of dynamically allocated memory space. If the function fails to execute successfully, such as insufficient memory space, a null pointer is returned

NULL.

int *p = (int *)malloc(4);

The system is requested to allocate 4 bytes of memory space, return the address of the first byte, and then assign it to the pointer variable P. When malloc is used to allocate dynamic memory, the above pointer variable p is initialized

It's melting.

2. sizeof(x) calculates the length of the variable x.

int *p = malloc(sizeof(int));

The value of sizeof (int) is the number of bytes occupied by int variables, which can well represent the number of bytes occupied by int variables in the current computer. In this way, the portability of writing programs is enhanced. So dynamic

It is best to build as much memory as you need.

3. Free (p) releases the storage space of the variable indicated by pointer p, that is, completely deletes a variable

A pointer variable pointing to dynamic memory was defined earlier p:

int *p = malloc(sizeof*(int));

As mentioned earlier, the dynamically allocated memory space is released manually by the programmer. So how to release it? Use the free function.

The free function has no return value. Its function is to release the memory unit pointed to by the pointer variable p. At this point, the memory unit pointed to by p will be released and returned to the operating system and will no longer be used by it.

The operating system can reassign it to other variables.

It should be noted that freeing does not mean emptying the memory space, but marking the memory space as "available" so that the operating system can reallocate it to other variables when allocating memory.

be careful:

Only dynamically created memory can be released with free, and static memory cannot be released with free. Static memory can only be released by the system.

Code implementation:

#include <stdio.h>
#include <stdlib.h>
#define InitSize 10 / / the initial length of the sequence table
typedef struct SqList
{
    /* data */
    int *data; //Use a static "array" to store data elements
    int MaxSize; //Define maximum length
    int length; //Current length of sequence table
};

void InitList(SqList &L)
{
    //Apply for a continuous piece of storage space with malloc function
    L.data = (int *)malloc(InitSize*sizeof(int));
    L.length = 0;
    L.MaxSize = InitSize;
}

void IncreaseSize(SqList &L, int len) {
    int *p = L.data;
    L.data = (int *)malloc((L.MaxSize + len)*sizeof(int));
    for (int i = 0; i < L.length; i++)
    {
        /* code */
        L.data[i] = p[i];  //Copy data to New Area
    }
    L.MaxSize = L.MaxSize + len; //Increase the maximum length of sequence table by len
    free(p);  //Free up the original memory space
    
}
int main()
{
    SqList L;    //Declare a sequence table
    InitList(L); //initialization
    //Insert element
    IncreaseSize(L, 5);
    return 0;
}

3. Sequence table features

1. Random access, that is, the ith element can be found in O(1) time. (code implementation: data[i-1]; static allocation and dynamic allocation are the same)
2. The storage density is high, and each node only stores data elements
3. It is inconvenient to expand the capacity (even if it is realized by dynamic allocation, the time complexity of expanding the length is relatively high)
4. Insertion and deletion operations are inconvenient, and a large number of elements need to be moved

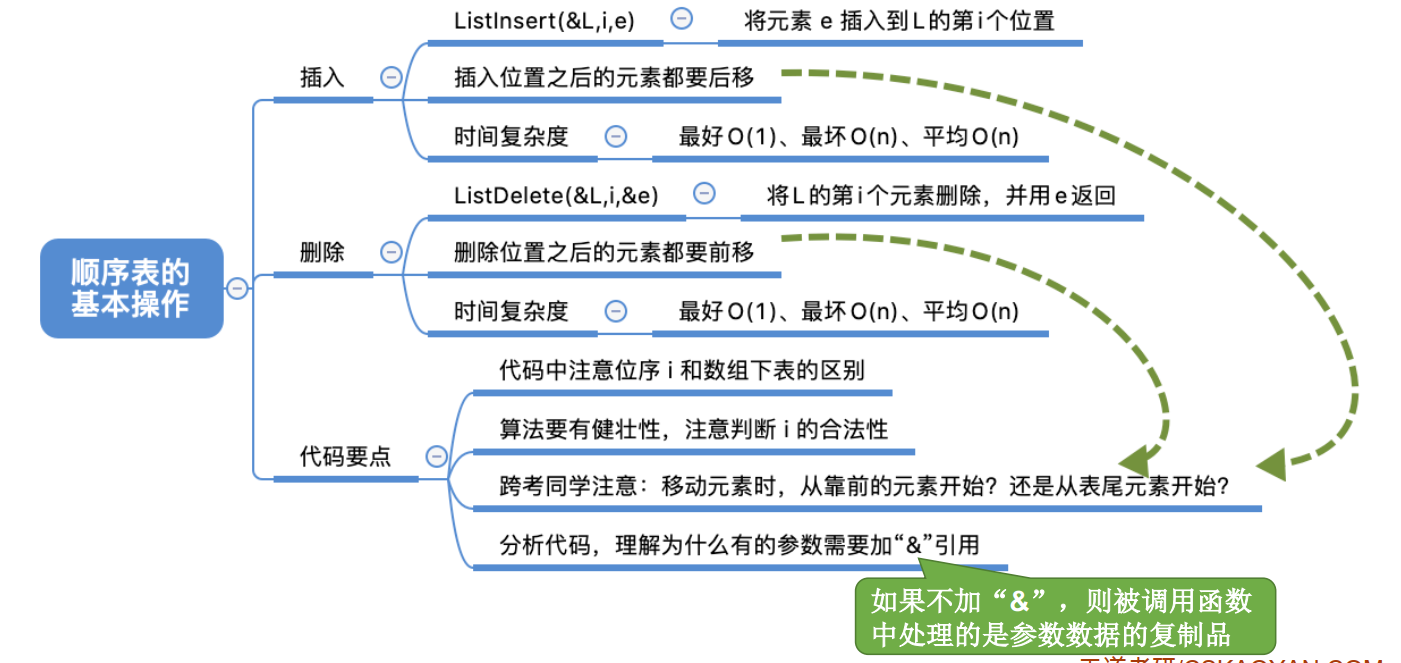
2.2.2 realization of basic operation

1. Insert

Listinsert (& L, i, e): insert operation. Insert the specified element E at position i in table L.

Code implementation:

#include<stdio.h>
#include<iostream>
#define MaxSize 10
using namespace std;
typedef struct
{
    /* data */
    int data[MaxSize];
    int length;
}SqList;

/**
 * initialization
 */
void InitList(SqList &L)
{
    L.length = 0; //The initial length of the sequence table is 0;
}

/**
 * Insert sequence table
 */
bool ListInsert(SqList &L, int i, int e) {
    //Judge whether the range of i is valid
    if (i < 1 || i > L.length + 1)
    {
        return false;
        /* code */
    }
    //Judge whether the current storage space is full and cannot be inserted
    if (L.length >= MaxSize) 
    {
        /* code */
        return false;

    }
    //Move the i th element and subsequent elements backward
    for (int j = L.length; j >= i; j--)
    {
        /* code */
        L.data[j] = L.data[j - 1];
    }
    //Place e at position i
    L.data[i - 1] = e;
    L.length++;  //Length++
    return true;
    
}

/**
 * Printout
 */ 
void printList(SqList L) {
    cout << "length length = " << L.length << endl;
    cout << "The data is:" << endl;
    for (int i = 0; i < L.length; i++)
    {
        /* code */
        cout << "data[" << i << "] = " << L.data[i] << endl;
        
    }
    
}
int main() {
    SqList L;
    InitList(L);
    //assignment
    for (int i = 0; i < 5; i++)
    {
        /* code */
        L.data[i] = i;
        L.length++;
    }
    printList(L);
    bool flag = ListInsert(L, 2, 6);
    cout << flag << endl;
    printList(L);
    return 0;
}

length length = 5
 The data is:
data[0] = 0
data[1] = 1
data[2] = 2
data[3] = 3
data[4] = 4
1
 length length = 6
 The data is:
data[0] = 0
data[1] = 6
data[2] = 1
data[3] = 2
data[4] = 3
data[5] = 4

Time complexity

1. Best case: the new element is inserted at the end of the table without moving the element

i = n+1, 0 cycles; Best time complexity = O(1)

2. Worst case: when a new element is inserted into the header, all the original n elements need to be moved backward

i = 1, N cycles; Worst time complexity = O(n)

3. Average case: suppose that the probability of inserting a new element into any position is the same, that is, the probability of i = 1,2,3,..., length+1 is p = 1 ( n + 1 ) p = \frac{1}{(n+1)} p=(n+1)1​

i = 1, N cycles; When i = 2, cycle n - 1; i = 3, cycle n-2 times... When i = n + 1, cycle 0 times

flat all Follow ring second number = n p + ( n − 1 ) p + ( n − 2 ) p + ... ... + 1 ⋅ p = n ( n + 1 ) 2 ∗ 1 ( n + 1 ) = n 2 Average number of cycles = np + (n-1)p + (n-2)p +... + 1 ⋅ p = \frac{n(n+1)}{2} * \frac{1}{(n+1)} = \frac{n}{2} Average number of cycles = np+(n − 1)p+(n − 2)p +... + 1 ⋅ p=2n(n+1) * (n+1)1 = 2n

Average time complexity = O(n)

2. Delete

ListDelete & L, i, & e: delete operation. Delete the element at position i in Table L and return the value of the deleted element with e.

Code implementation:

#include<stdio.h>
#include<iostream>
#define MaxSize 10
using namespace std;
typedef struct
{
    /* data */
    int data[MaxSize];
    int length;
}SqList;

/**
 * initialization
 */
void InitList(SqList &L)
{
    L.length = 0; //The initial length of the sequence table is 0;
}

/**
 * Delete sequence table
 */
bool ListDelete(SqList &L, int i, int &e) {
    //Judge whether the range of i is valid
    if (i < 1 || i > L.length + 1)
    {
        return false;
        /* code */
    }
    e = L.data[i - 1];
    //Move the i th element and subsequent elements forward
    for (int j = i; j < L.length; j++)
    {
        /* code */
        L.data[j - 1] = L.data[j];
    }
    L.length--;  //Length--
    return true;
    
}

/**
 * Printout
 */ 
void printList(SqList L) {
    cout << "length length = " << L.length << endl;
    cout << "The data is:" << endl;
    for (int i = 0; i < L.length; i++)
    {
        /* code */
        cout << "data[" << i << "] = " << L.data[i] << endl;
        
    }
    
}
int main() {
    SqList L;
    InitList(L);
    //assignment
    for (int i = 0; i < 5; i++)
    {
        /* code */
        L.data[i] = i;
        L.length++;
    }
    int e;
    printList(L);
    ListDelete(L, 4, e);
    printList(L);
    cout << "The number deleted is " << e << " " << endl;
    return 0;
}

length length = 5
 The data is:
data[0] = 0
data[1] = 1
data[2] = 2
data[3] = 3
data[4] = 4
 length length = 4
 The data is:
data[0] = 0
data[1] = 1
data[2] = 2
data[3] = 4
 The number deleted is 3

Time complexity

1. Best case: delete the footer element without moving other elements

i = n, 0 cycles; Best time complexity = O(1)

2. Worst case: to delete the header element, you need to move all the subsequent n-1 elements forward

i = 1, n-1 cycles; Worst time complexity = O(n)

3. Average case: suppose that the probability of deleting any element is the same, that is, the probability of i = 1,2,3,..., length is p = 1 n p = \frac{1}{n} p=n1​

i = 1, n-1 cycles; When i=2, cycle n-2 times; i=3, cycle n-3 times... When i =n, cycle 0 times

flat all Follow ring second number = ( n − 1 ) p + ( n − 2 ) p + ... ... + 1 ⋅ p = n ( n − 1 ) 2 ∗ 1 n = ( n − 1 ) 2 Average number of cycles = (n-1)p + (n-2)p +... + 1 ⋅ p = \frac{n(n-1)}{2} * \frac{1}{n} = \frac{(n-1)}{2} Average number of cycles = (n − 1)p+(n − 2)p +... + 1 ⋅ p=2n(n − 1) * n1 = 2(n − 1)

Average time complexity = O(n)

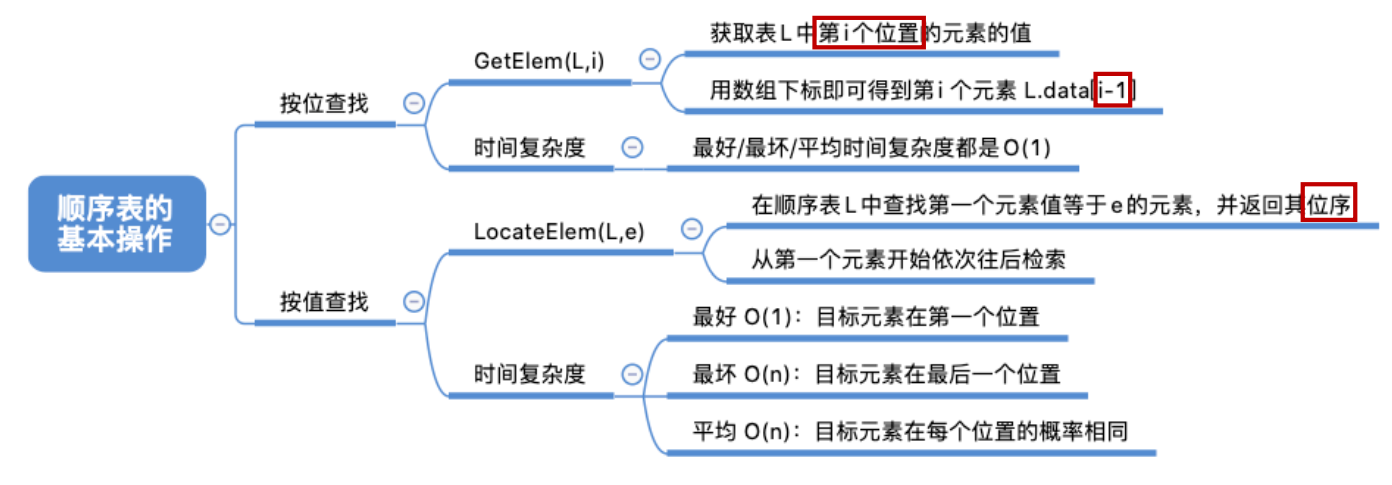
3. Search

(1) Search by bit

GetElem(L,i): bitwise lookup operation. Gets the value of the element at position i in table L.

Code implementation:

#include <stdio.h>
#include <stdlib.h>
#include <iostream>
#define InitSize 10
using namespace std;
typedef struct
{
    /* data */
    int *data; //Dynamic allocation
    int length;
    int MaxSize;
} SqList;

/**
 * initialization
 */
void InitList(SqList &L)
{
    L.data = (int *)malloc(InitSize*sizeof(int));
    L.MaxSize = InitSize;
    L.length = 0; //The initial length of the sequence table is 0;
}

/**
 * Bitwise lookup order table
 */
int ListSearchBySite(SqList L,  int i)
{
    cout << "Find page " << i << " The value of bit is:";
    return  L.data[i - 1];
}

/**
 * Printout
 */
void printList(SqList L)
{
    cout << "length length = " << L.length << endl;
    cout << "The data is:" << endl;
    for (int i = 0; i < L.length; i++)
    {
        /* code */
        cout << "data[" << i << "] = " << L.data[i] << endl;
    }
}

int main()
{
    SqList L;
    InitList(L);
    //assignment
    for (int i = 0; i < 5; i++)
    {
        /* code */
        L.data[i] = i;
        L.length++;
    }
    printList(L);
    cout << ListSearchBySite(L, 3) << endl;
    return 0;
}

length length = 5
 The data is:
data[0] = 0
data[1] = 1
data[2] = 2
data[3] = 3
data[4] = 4
 Find the value of bit 3: 2

Time complexity

Since each data element of the sequence table is stored continuously in memory, the i-th element - "random access" feature can be found immediately according to the starting address and the size of the data element

Time complexity = O(n)

(2) Find by value

Locaterelem (L, e): find operation by value. Finds an element with a given keyword value in table L.

Code implementation:

#include <stdio.h>
#include <stdlib.h>
#include <iostream>
#define InitSize 10
using namespace std;
typedef struct
{
    /* data */
    int *data;
    int length;
    int MaxSize;
} SqList;

/**
 * initialization
 */
void InitList(SqList &L)
{
    L.data = (int *)malloc(InitSize * sizeof(int));
    L.MaxSize = InitSize;
    L.length = 0; //The initial length of the sequence table is 0;
}

/**
 * Lookup order table by value
 */
int ListSearchByValue(SqList L, int e)
{
    cout << "The lookup value is " << e << " The location of the is:";
    for (int i = 0; i < L.length; i++)
        if (L.data[i] == e)
            return i + 1; //The value of the element with the index i of the array is equal to e, and its bit order i+1 is returned
    return 0;             //Exit the loop, indicating that the search failed
}


/**
 * Printout
 */
void printList(SqList L)
{
    cout << "length length = " << L.length << endl;
    cout << "The data is:" << endl;
    for (int i = 0; i < L.length; i++)
    {
        /* code */
        cout << "data[" << i << "] = " << L.data[i] << endl;
    }
}

int main()
{
    SqList L;
    InitList(L);
    //assignment
    for (int i = 0; i < 5; i++)
    {
        /* code */
        L.data[i] = i;
        L.length++;
    }
    printList(L);
    cout << ListSearchByValue(L, 1) << endl;
    return 0;
}

length length = 5
 The data is:
data[0] = 0
data[1] = 1
data[2] = 2
data[3] = 3
data[4] = 4
 The location where the lookup value is 1 is: 2

Time complexity

1. Best case: the target element circulates once in the header; Best time complexity = O(1);

2. Worst case: the target element circulates n times at the end of the table; Worst time complexity = O(n);

3. Average case: assuming that the probability of the target element appearing at any position is the same, it is the same 1 n \frac{1}{n} n1​

flat all Follow ring second number = n p + ( n − 1 ) p + ( n − 2 ) p + ... ... + 1 ⋅ p = n ( n + 1 ) 2 ∗ 1 n = ( n + 1 ) 2 Average number of cycles = np + (n-1)p + (n-2)p +... + 1 ⋅ p = \frac{n(n+1)}{2} * \frac{1}{n} = \frac{(n+1)}{2} Average number of cycles = np+(n − 1)p+(n − 2)p +... + 1 ⋅ p=2n(n+1) * n1 = 2(n+1)

Average time complexity = O(n)

A blog post on time complexity analysis is attached
Data structure - Introduction (II) -- time complexity analysis