Heap heap introduction
concept
Heap is a special tree based data structure, in which the tree is a complete binary tree. In general, there are two types of heaps:
- Max heap large top heap: in Max heap, the key on the root node must be the largest of the keys on all child nodes. The same properties must apply recursively to all subtrees in the binary tree.
- Min heap small top heap: in Min heap, the key on the root node must be the smallest of the keys on all its child nodes. The same properties must apply recursively to all subtrees in the binary tree
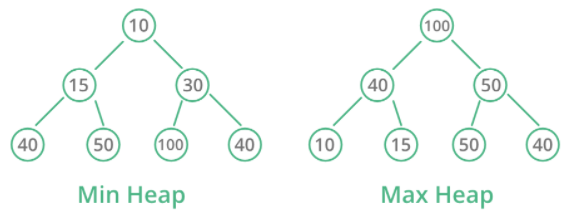
Characteristics of reactor
The heap satisfies the following properties: see heap-data-structure
- Heap is a complete binary tree, also known as binary heap. Generally speaking, heap refers to binary heap. In fact, there are left leaning heap and right leaning heap. They are not required to be a complete binary tree.
- The value of any node in the heap is always not greater than / less than the value of its child nodes;
Heap application scenario
- Heap is often used to implement "priority queue". Priority queues are free to add data
- In guava package, there is a two-way priority queue (MinMaxPriorityQueue), which provides a way to access the data structure of its smallest and largest elements with constant time complexity. As a queue, it is functionally the same as PriorityQueue
- PriorityQueue (priority queue) is essentially a minimum heap, which is different from first in first out (FIFO) queue. Each time the element with the highest priority is taken out of the queue (specify the comparator).
- Implement heap sorting
Implementation of heap
Because the heap is a complete binary tree
According to the nature of the binary tree, the complete binary tree can be perfectly mapped to the array structure: if the nodes are numbered from 0 and mapped to the array, the nodes meet the following relationship:
- Large top pile: arr [i] > = arr [2I + 1] & & arr [i] > = arr [2I + 2] (0 < = I < = n / 2 - 1), such as 9,8,7,6,5,4,3,2,1
- Small top pile: arr [i] < = arr [2I + 1] & & arr [i] < = arr [2I + 2] (0 < = I < = n / 2 - 1), such as 1,2,3,4,5,6,7,8,9
n is the length of the array, and n/2 -1 actually represents the index position of the last non leaf node of the array from beginning to end.
Therefore, arrays are often used to implement the heap structure. For example, PriorityQueue in Java is a binary heap implemented by arrays.
Because the heap is regarded as a partial order (only the size relationship between the parent node and the child node, and there is no size relationship between the two child nodes), the actual storage order of the heap constructed by the same batch of elements using different algorithms in the array is not necessarily the same, and heap sorting is also an unstable sorting algorithm.
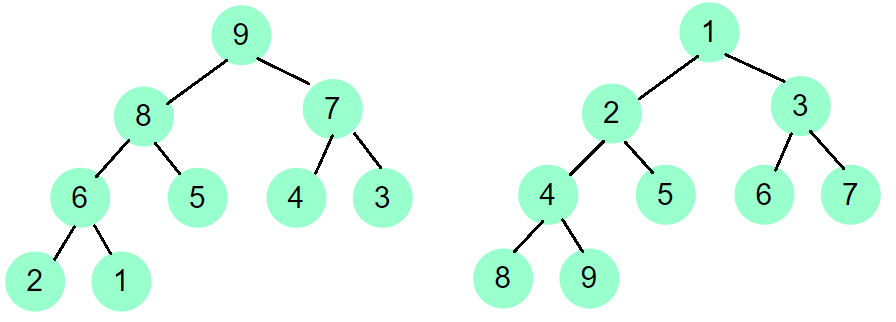
Differences between binary sort trees:
- In a binary sort tree, the left child node must be smaller than the parent node and the right child node must be larger than the parent node. But not in the heap. In the largest heap, both child nodes must be smaller than the parent node, while in the smallest heap, both must be larger than the parent node
- Binary sort trees are generally implemented by linked lists, which occupy more memory space than the data they store. Additional memory must be allocated for node objects and left / right child node pointers. The heap can use arrays to store data. There is a natural relationship between node objects and left / right child nodes, which can be reached by using indexes to save memory.
- Due to the nature of the node size in the binary sort tree, the search in the binary sort tree will be fast. The search process is similar to the binary search of an ordered array, and the search times will not exceed the depth of the tree, but the search in the heap will be slow. The purpose of using binary sort tree is to find nodes conveniently. The purpose of using heap is to put the largest (or smallest) node in the front, so as to quickly sort, insert and delete.
code implementation
Large top stack implementation
import java.util.Arrays;
import java.util.Collection;
import java.util.Comparator;
public class MaxBinaryTreeHeap<E> {
private Object[] heap;
private int size;
/**
* If the initial capacity is not specified, the default is 16
*/
private static int capacity = 16;
/**
* If the element uses natural sorting, the comparator is null; Otherwise, a comparator is used for comparison
*/
private final Comparator<? super E> cmp;
/**
* For the method of comparing the size of elements, if a user-defined comparator is passed, the user-defined comparator is used; otherwise, the data type is required to implement the Comparable interface
*
* @param e1 The first object to be compared
* @param e2 The second object being compared
* @return 0 equal; Less than 0 E1 < E2; Greater than 0 E1 > E2
*/
private int compare(E e1, E e2) {
if (cmp != null) {
return cmp.compare(e1, e2);
} else {
return ((Comparable<E>) e1).compareTo(e2);
}
}
/**
* Initialize the empty large top heap and use the default capacity
*/
public MaxBinaryTreeHeap() {
this(capacity, null);
}
/**
* Initialize the empty large top heap and specify the capacity
*
* @param initCapacity Specify capacity array
*/
public MaxBinaryTreeHeap(int initCapacity) {
this(initCapacity, null);
}
/**
* Initialize the empty large top heap and specify the comparator
*
* @param comparator Specify comparator
*/
public MaxBinaryTreeHeap(Comparator<? super E> comparator) {
this(capacity, comparator);
}
/**
* Initialize the empty large top heap, specify the capacity and comparator
*
* @param initCapacity Specify array capacity
* @param comparator Specify comparator
*/
public MaxBinaryTreeHeap(int initCapacity, Comparator<? super E> comparator) {
if (initCapacity < 1) {
throw new IllegalArgumentException();
}
capacity = initCapacity;
this.heap = new Object[initCapacity];
cmp = comparator;
}
/**
* Initialize the large top heap through the same batch of data
*
* @param heap array
*/
public MaxBinaryTreeHeap(Collection<? extends E> heap) {
this(heap, null);
}
/**
* Initialize the large top heap through the same batch of data and the specified comparator
*
* @param heap array
* @param comparator Custom comparator
*/
public MaxBinaryTreeHeap(Collection<? extends E> heap, Comparator<? super E> comparator) {
Object[] array = heap.toArray();
this.cmp = comparator;
if (array.getClass() != Object[].class) {
array = Arrays.copyOf(array, array.length, Object[].class);
}
for (Object o : array) {
if (o == null) {
throw new NullPointerException();
}
}
this.heap = array;
this.size = array.length;
buildHeap(this.heap);
}
/**
* Initialize the large top heap through the same batch of data
*
* @param heap Data array
*/
private void buildHeap(Object[] heap) {
/*i Starting from the index of the last non leaf node, decrement the build until i=-1 ends the loop
Here, the index of the element starts from 0, so the last non leaf node array.length/2 - 1 takes advantage of the nature of a complete binary tree*/
for (int i = heap.length / 2 - 1; i >= 0; i--) {
buildHeap(heap, i, heap.length);
}
}
/**
* Initialize large top heap
*
* @param arr Data array
* @param i Index of non leaf node
* @param length Heap length
*/
private void buildHeap(Object[] arr, int i, int length) {
//Take out the current non leaf node element first, because the current element may have to move all the time
Object temp;
//The index of the child node of the node
int childIndex;
/*The loop judges whether the parent node is greater than two child nodes. If the index of the left child node is greater than or equal to the heap length or the parent node is greater than two child nodes, the loop ends*/
for (temp = arr[i]; (childIndex = 2 * i + 1) < length; i = childIndex) {
//childIndex + 1 < length indicates that the node has a right child node. If the value of the right child node is greater than the left child node, the childIndex will increase by 1, that is, the childIndex points to the index of the right child node
if (childIndex + 1 < length && compare((E) arr[childIndex], (E) arr[childIndex + 1]) < 0) {
childIndex++;
}
//If it is found that the maximum child node (left and right child nodes) is greater than the root node, in order to ensure that the value of the root node of the large top heap is greater than that of the child node, it is necessary to exchange values
//If the child node is replaced, the subtree with the child node as the root will be affected. Therefore, after the exchange, continue to cycle to judge the tree where the child node is located
if (compare((E) arr[childIndex], (E) temp) > 0) {
swap(arr, i, childIndex);
} else {
//Here, it shows that the parent node is larger than the largest child node, meets the condition of large top heap, and directly terminates the cycle
break;
}
}
}
/**
* Large top heap sort (order)
* In fact, it is a process of continuously cycling to exchange the top and tail elements, then remove the tail elements, and then reconstruct the large top heap
*/
public Object[] heapSort() {
//Sort output using a copy of the large top heap
Object[] arr = Arrays.copyOf(heap, size);
/*Start heap sorting, i = arr.length - 1, that is, start from the number at the tail of the large top heap until i=0 to end the cycle*/
for (int i = size - 1; i > 0; i--) {
//Swap top and tail element order
swap(arr, 0, i);
//Rebuild the large top reactor
buildHeap(arr, 0, i);
}
return arr;
}
/**
* Add nodes to build a large top heap
*
* @param e Nodes to be added
*/
public void add(E e) {
/*Air judgment*/
if (e == null) {
throw new NullPointerException();
}
/*Check capacity*/
if (heap.length == size) {
resize();
}
/*Add node*/
addNode(e, size++);
}
/**
* Add nodes and reconstruct the large top heap upward. Finally, find a location to add a new node e, where the node is less than or equal to its parent node
*
* @param e Node to add
*/
private void addNode(E e, int start) {
//Gets the parent node index of the node at size
int parent = (start - 1) / 2;
/*If size > 0, find a suitable location: the new node at an inserted location is less than or equal to the value of the corresponding parent node*/
while (start > 0) {
//Judge the size of the parent node and the new child node. If the parent node is less than or equal to the new child node, it meets the requirements of the small top heap. The reconstruction ends, and the start is the insertion position of the child node
if (compare((E) heap[parent], e) >= 0) {
break;
} else {
//Otherwise, move the value of the parent node to the position of the child node
heap[start] = heap[parent];
//Change the index value of start to the index value of the parent node
start = parent;
//Recalculate the index of the parent node and cycle until the index with the parent node value less than or equal to the value of the new child node is found
parent = (start - 1) / 2;
}
}
//Insert the new node value in the appropriate location
heap[start] = e;
}
/**
* Expansion of underlying array
*/
private void resize() {
heap = Arrays.copyOf(heap, heap.length * 2, Object[].class);
}
/**
* Exchange element
*
* @param arr array
* @param a Subscript of element
* @param b Subscript of element
*/
private static void swap(Object[] arr, int a, int b) {
Object temp = arr[a];
arr[a] = arr[b];
arr[b] = temp;
}
/**
* Delete the first heap node found and reconstruct the large top heap
*
* @param e Nodes to be deleted
* @return false Delete failed. Delete succeeded
*/
public boolean remove(E e) {
int eIndex = -1;
for (int i = 0; i < size; i++) {
//Here, compare is used to find whether the elements are the same
if (compare((E) heap[i], e) == 0) {
eIndex = i;
}
}
/*No element found to delete*/
if (eIndex == -1) {
return false;
}
/*eureka*/
//Original tail element x
E x = (E) heap[size - 1];
//Swap the location of the found element and the heap tail element
swap(heap, eIndex, size - 1);
//Remove tail element
heap[size--] = null;
//Rebuild the large top heap downward from eIndex
buildHeap(heap, eIndex, size);
//After construction, if the element at eIndex position is x, it indicates that the heap structure has not been adjusted, then the element at this position is regarded as a newly inserted element, and the large top heap needs to be constructed upward
if (heap[eIndex] == x) {
//Call addNode to reconstruct the large top heap upward from eIndex
addNode(x, eIndex);
}
return true;
}
public int size() {
return size;
}
@Override
public String toString() {
StringBuilder stringBuilder = new StringBuilder();
stringBuilder.append("[");
for (int i = 0; i < size; i++) {
stringBuilder.append(heap[i]);
if (i != size - 1) {
stringBuilder.append(",");
}
}
stringBuilder.append("]");
return stringBuilder.toString();
}
}
Small top stack implementation
Please refer to the implementation of the PriorityQueue class
Test code
public static void main(String[] args) {
Integer[] arr = new Integer[]{9, 8, 5, 4, 5, 2, 1, 3, 7};
//Construction of large top reactor
MaxBinaryTreeHeap<Integer> maxBinaryHeap = new MaxBinaryTreeHeap<>(Arrays.asList(arr));
//Output large top reactor
System.out.println(maxBinaryHeap);
//Add nodes and refactor the large top heap
maxBinaryHeap.add(11);
maxBinaryHeap.add(77);
//Output large top reactor
System.out.println(maxBinaryHeap);
//Delete the node and reconstruct the large top heap
//Deletion failed
System.out.println(maxBinaryHeap.remove(79));
//Delete succeeded
System.out.println(maxBinaryHeap.remove(7));
//Output large top reactor
System.out.println(maxBinaryHeap);
//Large top heap sort (sequential sort)
System.out.println(Arrays.toString(maxBinaryHeap.heapSort()));
//Output large top reactor
System.out.println(maxBinaryHeap);
}
The output results are as follows:
[9,8,5,7,5,2,1,3,4]
[77,11,5,7,9,2,1,3,4,5,8]
false
true
[77,11,5,8,9,2,1,3,4,5]
[1, 2, 3, 4, 5, 5, 8, 9, 11, 77]
[77,11,5,8,9,2,1,3,4,5]
reference resources
Detailed explanation of the principles of 10 common sorting algorithms and the complete implementation of Java code
heap-data-structure