Some of the algorithms in the figure are relatively complex, which is summarized in multiple blogs

Related concepts of Graphs

In fact, the previous data structures are relatively simple, and the previous memory is still relatively clear. However, some concepts are a little fuzzy when it comes to the figure. Here, we will summarize the relevant concepts in the figure below.

Definition

Definition: a graph is composed of some points (vertex) and the edge between them; where points are usually referred to as "vertex", and the connection between points is referred to as "edege". Usually, G=(V,E).

According to whether the edge has direction, it can be divided into directed graph and undirected graph

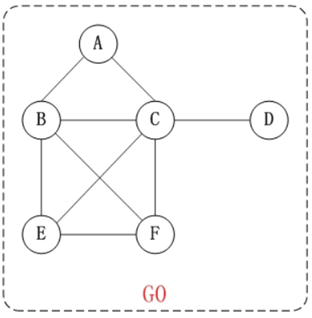
Undirected graph

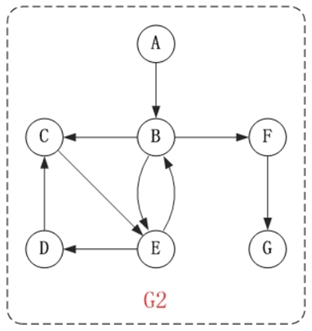
Digraph

Adjacency point and degree

Adjacency point

Two vertices on an edge are called adjacency points.
For example, vertex A and vertex C in the above undirected graph G0 are adjacency points.

In digraphs, in addition to adjacency points, there are also the concepts of "in edge" and "out edge".
The in edge of a vertex refers to the edge that ends at that vertex. The outgoing edge of a vertex refers to the edge starting from the vertex.
*For example, B and E in digraph G2 above are adjacency points; * * * is the out edge of B or the in edge of E.

degree

In an undirected graph, the degree of a vertex is the number of edges (or arcs) adjacent to that vertex.
For example, the degree of vertex A in the undirected graph G0 above is 2.

In digraphs, degrees can be divided into in degrees and out degrees.
The degree of penetration of a vertex refers to the number of edges ending at that vertex. The vertex degree refers to the number of edges starting from the vertex.
Vertex degree = in degree + out degree.
For example, in the digraph G2 above, the degree of entry and exit of vertex B is 2 and 3; the degree of vertex b * = 2 + 3 = 5 * *. *

How to store graphs

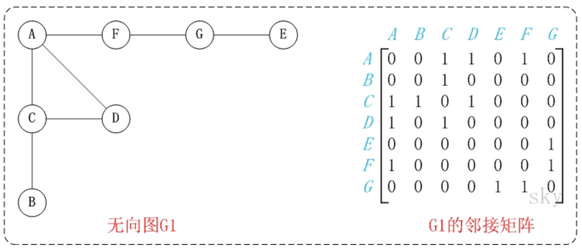
adjacency matrix

Adjacency matrix refers to using matrix to represent graph. It uses matrix to describe the relationship between vertices (and the weight of arc or edge).
If the number of vertices in the graph is n, the adjacency matrix is defined as:

Generally, two arrays are used to realize adjacency matrix: one is used to store vertex information, and the other is used to store edge information.
The disadvantage of adjacency matrix is that it consumes more space.

Adjacency matrix of undirected graph

Relevant code design

public class MatrixDG {
    int size;
    char[] vertexs; //Figure vertex name
    int[][] matrix; //Graph relation matrix
}

Specific construction methods

/**
 * autor:liman
 * createtime:2020/2/9
 * comment: Array representation of undirected graph
 */
public class MatrixNDG {

    int size;
    char[] vertexs; //Figure vertex name
    int[][] matrix; //Graph relation matrix

    public MatrixNDG(char[] vertexs, char[][] edges) {
        size = vertexs.length;
        matrix = new int[size][size];
        this.vertexs = vertexs;

        for (char[] c : edges) {
            int p1 = getPosition(c[0]);
            int p2 = getPosition(c[1]);

            //Undirected graph, two symmetrical positions need to be stored
            matrix[p1][p2] = 1;
            matrix[p2][p1] = 1;
        }
    }

    public void print() {
        for (int[] i : matrix) {
            for (int j : i) {
                System.out.print(j + " ");
            }
            System.out.println();
        }
    }

    //Get the corresponding matrix subscript according to the vertex name
    private int getPosition(char ch) {
        for (int i = 0; i < vertexs.length; i++) {
            if (vertexs[i] == ch) {
                return i;
            }
        }
        return -1;
    }

    public static void main(String[] args) {
        char[] vexs = {'A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'I', 'J', 'K'};
        char[][] edges = new char[][]{
                {'A', 'C'},
                {'A', 'D'},
                {'A', 'F'},
                {'B', 'C'},
                {'C', 'D'},
                {'E', 'G'},
                {'D', 'G'},
                {'I', 'J'},
                {'J', 'G'},
                {'E', 'H'},
                {'H', 'K'}};

        MatrixNDG matrixNDG = new MatrixNDG(vexs,edges);
        matrixNDG.print();
    }
}

Adjacency matrix of digraph

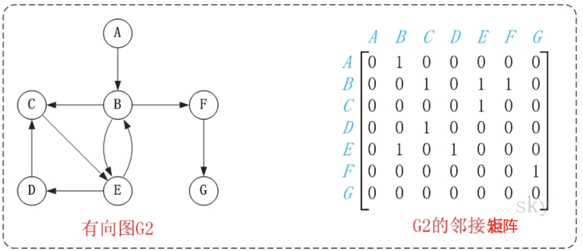
The construction and storage structure of the digraph is the same as the above, but there is only one line less code during construction, as follows:

public MatrixDG(char[] vertexs, char[][] edges) {
    size = vertexs.length;
    matrix = new int[size][size];
    this.vertexs = vertexs;

    for (char[] c : edges) {
        int p1 = getPosition(c[0]);
        int p2 = getPosition(c[1]);

        //Directed graph, only need to store one
        matrix[p1][p2] = 1;
    }
}

Adjacency list

Adjacency table is a kind of chain storage representation method of graph. It is an improved "adjacency matrix". Its disadvantage is that it is not convenient to judge whether there is edge between two vertices, but it is more space saving than adjacency matrix.

Adjacency table of undirected graph

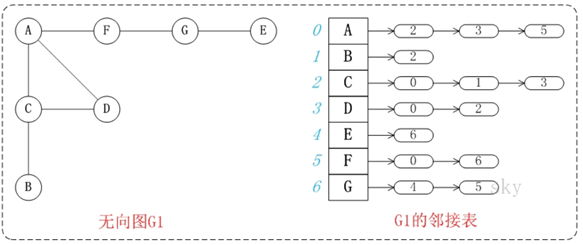
Specific storage design

/**
 * autor:liman
 * createtime:2020/2/9
 * comment: Storage of undirected graph by adjacency table
 */
public class ListNDG {

    Vertex[] vertexList;	//Here is an array of storage nodes
    int size;

    class Vertex{
        char ch;
        Vertex next;

        public Vertex(char ch) {
            this.ch = ch;
        }

        void add(char ch){
            Vertex node = this;
            while(node.next!=null){//Find the end of the list
                node = node.next;
            }
            node.next = new Vertex(ch);
        }
    }
}

The specific construction operations are as follows:

public ListNDG(char[] vertexs,char[][] edgs){
    size = vertexs.length;
    this.vertexList = new Vertex[size];//Determine size of adjacency table
    //Set each node of adjacency table
    for(int i = 0;i<size;i++){
        this.vertexList[i] = new Vertex(vertexs[i]);
    }

    //Storage side information
    for(char[] c:edgs){
        int p1 = getPosition(c[0]);
        vertexList[p1].add(c[1]);
        int p2 = getPosition(c[1]);
        vertexList[p2].add(c[0]);
    }
}

//Get the list subscript according to the vertex name
private int getPosition(char ch){
    for(int i =0;i<size;i++){
        if(vertexList[i].ch==ch){
            return i;
        }
    }
    return -1;
}

public void print(){
    for(int i = 0;i<size;i++){
        Vertex temp = vertexList[i];
        while(temp!=null){
            System.out.print(temp.ch+" ");
            temp = temp.next;
        }
        System.out.println();
    }
}

public static void main(String[] args) {
    char[] vexs = {'A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'I', 'J', 'K'};
    char[][] edges = new char[][]{
            {'A', 'C'},
            {'A', 'D'},
            {'A', 'F'},
            {'B', 'C'},
            {'C', 'D'},
            {'E', 'G'},
            {'D', 'G'},
            {'I', 'J'},
            {'J', 'G'},
            {'E', 'H'},
            {'H', 'K'}};

    ListNDG listNDG = new ListNDG(vexs,edges);
    listNDG.print();
}

Adjacency table of Digraphs

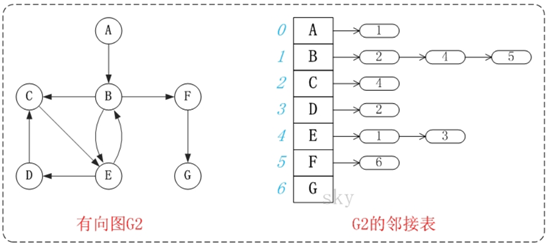
In the same way as adjacency matrix, it is two lines less than undirected graph

public ListDG(char[] vertexs, char[][] edgs){
    size = vertexs.length;
    this.vertexList = new Vertex[size];//Determine size of adjacency table
    //Set each node of adjacency table
    for(int i = 0;i<size;i++){
        this.vertexList[i] = new Vertex(vertexs[i]);
    }

    //This is a directed graph that stores only one-way connection edge information
    for(char[] c:edgs){
        int p1 = getPosition(c[0]);
        vertexList[p1].add(c[1]);
    }
}