1. Realization of Adjacency Matrix of Graphs

1. Graph with vertex array and adjacency matrix as storage structure is realized.

2. The algorithms of graph creation (including directed/undirected graph, directed/undirected network), vertex/edge addition and deletion, depth/breadth first traversal are implemented.

3. Initialize the creation of graph by using vertex object list and edge (arc) object list. Refer to "ObjArrayList.h" header file, the header file can refer to the previous blog "Order List of Data Structures (Supporting Object Elements)" code.

4. To solve the problem of discontinuous storage of vertices in array (static) by indexing the subscripts of empty vertex arrays into a queue, and referring to the header file "LinkQueue.h", the header file can refer to the previous blog article "Queue of Data Structure (Class Template Implementation of Circular Queue and Chain Queue)".

5. Depth-first traversal is implemented by recursive algorithm, while breadth-first traversal is implemented by queuing.

6. In the test code, all weighted edges of the directed network are used as the initialization data. Selecting graph types (DG, UDG, DN, UDN) can create different types of graphs.
 

2. Graph Structural Diagram in Test Code

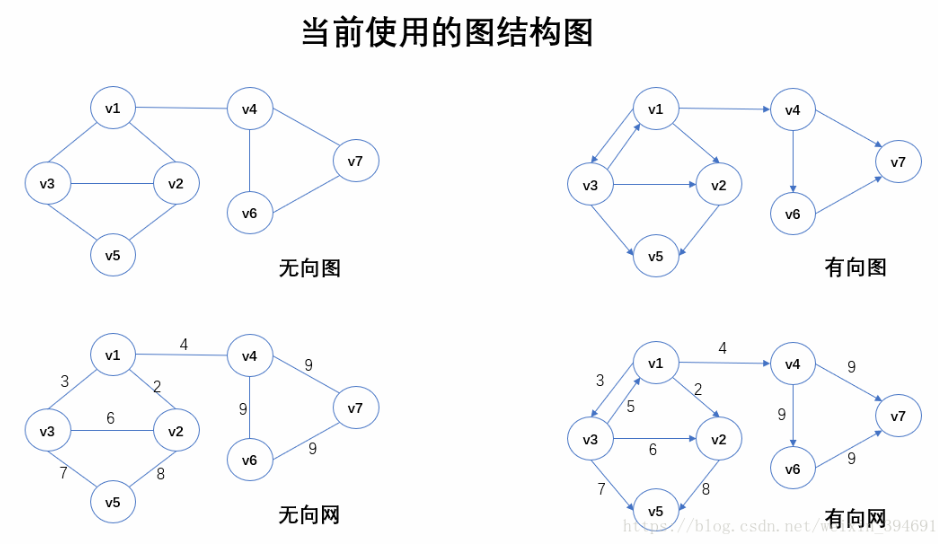
Depth-first traversal sequence (starting from v1 vertex):

1. undirected graph/network: v1-v2-v3-v5-v4-v6-v7

2. Directed graph/network: v1-v2-v5-v3-v4-v6-v7

Breadth-first traversal sequence (starting from v2 vertex):

1. undirected graph/network: v2-v1-v3-v5-v4-v6-v7

2. Directed graph/network: v2-v5 postorder cannot be traversed

Note: The traversal of a digraph follows the direction of outgoing traversal. If there is no direction of outgoing traversal, the traversal terminates.

Three, code

//File name: "GraphAdjMat.h"
#pragma once
#ifndef GRAPHADJMAT_H_
#define GRAPHADJMAT_H_
 
#include <limits>
#include <string>
#include "ObjArrayList.h"
#include "LinkQueue.h"
using namespace std;
 
/*
.	Graph Adjacency Matrix
.	Relevant terms:
.		Vertex; Edge Arc; Weight;
.		Digraph of digraph;Undigraph of undirected graph;
.		Directed Network; Undirected Network;
*/
 
class GraphAdjMat
{
	/*
	.	Edge (arc) element, note: adjacent matrix element
	*/
	struct ArcCell
	{
		int adj;		//Adjacent vertex relations. Graph: 0 | Neighbor 1 | Neighbor; Network: Infinite (INT_MAX) | Neighbor Weight (W) | Neighbor
		char * info;	//Edge (arc) information
	};
	
public:
	/*
	.	Types of Graphs
	*/
	enum GraphType
	{
		DG,			//Directed graph, default 0
		UDG,		//Undirected graph, default 1
		DN,			//Directed network, default 2
		UDN			//Undirected network, default 3
	};
	/*
	.	Edge (arc) data, note: for external initialization of edge data
	*/
	struct ArcData
	{
		string Tail;	//Arc tail
		string Head;	//Arc head
		int Weight;		//weight
	};
 
private:
	const int _INFINITY = INT_MAX;				//Infinite Notes: Included in Header File < limits >
	static const int _MAX_VERTEX_NUM = 10;		//Supporting maximum number of vertices
 
	//Static storage structure
	string vexs[_MAX_VERTEX_NUM];						//Vertex table
	ArcCell arcs[_MAX_VERTEX_NUM][_MAX_VERTEX_NUM];		//Edge (Arc) Matrix
	int vexNum;			//Vertex number
	int arcNum;			//Edge number
	int type;			//Types of Graphs
	int nonAdjInt;		//Non-adjacent int: 0 | Infinite without power | Right
 
	LinkQueue<int> *vexs_null_index_queue = new LinkQueue<int>();		//Hollow vertex position index queue in vertex array (need to be destroyed)
	bool vexs_visited[_MAX_VERTEX_NUM];			//Vertex Access Markup Array: 0 | Not Accessed 1 | Accessed
 
	void _CreateDG(ObjArrayList<ArcData> * arcsList);			//Creating Directed Graphs
	void _CreateUDG(ObjArrayList<ArcData> * arcsList);			//Create undirected graph
	void _CreateDN(ObjArrayList<ArcData> * arcsList);			//Creating Directed Networks
	void _CreateUDN(ObjArrayList<ArcData> * arcsList);			//Creating undirected network
	
	int _Locate(string vertex);					//Location of vertex elements
	void _DFS_R(int index);						//Depth-first traversal recursion
 
public:
	GraphAdjMat(int type);						//Constructor: Initialization graph type
	~GraphAdjMat();								//Destructor: Destruction Graph Storage Space
	void Init(ObjArrayList<string> * vexs, ObjArrayList<ArcData> * arcsList);		//Initialize vertex and edge data as graph | net
	void Display();								//Display Chart | Net
	void InsertVertex(string *vertex);			//Insert a new vertex
	void DeleteVertex(string *vertex);			//Delete a vertex
	void InsertArc(ArcData *arc);				//Insert a new edge (arc)
	void DeleteArc(ArcData *arc);				//Delete an edge (arc)
	void Display_DFS(string *vertex);			//Beginning with the specified vertex, depth first traversal
	void Display_BFS(string *vertex);			//Starting with the specified vertex, breadth-first traversal
 
	GraphAdjMat * MiniSpanTree_Prim(string * vertex);		//Minimum Spanning Tree (Prim algorithm)
	GraphAdjMat * MiniSpanTree_Kruskal(string * vertex);	//Minimum Spanning Tree (Kruskal algorithm)
 
};
 
#endif // !GRAPHADJMAT_H_

//File name: "GraphAdjMat.cpp"
#include "stdafx.h"
#include <string>
#include "ObjArrayList.h"
#include "LinkQueue.h"
#include "GraphAdjMat.h"
using namespace std;
 
GraphAdjMat::GraphAdjMat(int type)
{
	/*
	.	Constructor: Initialization graph type
	*/
	this->type = type;
	this->vexNum = 0;
	this->arcNum = 0;
	if (this->type == DG || this->type == UDG)
	{
		//Non-adjacent int value 0 of Graphs
		this->nonAdjInt = 0;
	}
	else
	{
		//The Neighboring int Value of a Network is Infinite
		this->nonAdjInt = this->_INFINITY;
	}
}
 
GraphAdjMat::~GraphAdjMat()
{
	/*
	.	Destructor: Destruction Chart
	*/
	//1. Release vertex empty location index queue
	int * e;
	while (vexs_null_index_queue->GetHead() != NULL)
	{
		e = vexs_null_index_queue->DeQueue();
		delete e;
	}
	delete vexs_null_index_queue;
 
}
 
void GraphAdjMat::Init(ObjArrayList<string> * vexs, ObjArrayList<ArcData> * arcsList)
{
	/*
	.	Initialize vertices, edge data, and build chart|network
	.	Participation:
	.		vexs: Vertex list
	.		arcsList: Edge Data List
	*/
	//1. Initialize vertex data
	if (vexs->Length() > this->_MAX_VERTEX_NUM)
	{
		return;
	}
	for (int i = 0; i < vexs->Length(); i++)
	{
		this->vexs[i] = *vexs->Get(i);
	}
	this->vexNum = vexs->Length();
	//1.1. Initialize the null vertex position index queue of vertex array
	for (int i = vexs->Length(); i < _MAX_VERTEX_NUM; i++)
	{
		vexs_null_index_queue->EnQueue(new int(i));
	}
	//2. Create the specified graph according to the initialized graph type
	switch (this->type)
	{
	case DG:
		_CreateDG(arcsList); break;
	case UDG:
		_CreateUDG(arcsList); break;
	case DN:
		_CreateDN(arcsList); break;
	case UDN:
		_CreateUDN(arcsList); break;
	default:
		break;
	}
}
 
void GraphAdjMat::_CreateDG(ObjArrayList<ArcData> * arcsList)
{
	/*
	.	Creating Directed Graphs
	.	Vertex adjacency: 0 | non-adjacent 1 | adjacent
	.	Adjacent Matrix is Asymmetric Matrix
	*/
	//Initialize temporary edge objects
	ArcData * arcData = NULL;
	//Initialization Matrix Two-Dimensional Coordinates
	int m = 0, n = 0;
	//Adjacency Matrix of Initialization Edge
	for (int i = 0; i < _MAX_VERTEX_NUM; i++)
	{
		for (int j = 0; j < _MAX_VERTEX_NUM; j++)
		{
			this->arcs[i][j].adj = 0;
			this->arcs[i][j].info = NULL;
		}
	}
	//Traversing Edge Data List
	for (int i = 0; i < arcsList->Length(); i++)
	{
		//Sequential acquisition of edges (arcs)
		arcData = arcsList->Get(i);
		//Locate (or set) the vertex positions at both ends of the edge
		m = _Locate(arcData->Tail);
		n = _Locate(arcData->Head);
		//Set vertex adjacent to 1 (undirected)
		if (this->arcs[m][n].adj == 1)
		{
			//Remove duplicate edges
			continue;
		}
		this->arcs[m][n].adj = 1;
		//Edge count
		this->arcNum++;
	}
}
 
void GraphAdjMat::_CreateUDG(ObjArrayList<ArcData> * arcsList)
{
	/*
	.	Create undirected graph
	.	Vertex adjacency: 0 | non-adjacent 1 | adjacent
	.	Adjacency matrix is symmetric matrix
	*/
	//Initialize temporary edge objects
	ArcData * arcData = NULL;
	//Initialization Matrix Two-Dimensional Coordinates
	int m = 0, n = 0;
	//Adjacency Matrix of Initialization Edge
	for (int i = 0; i < _MAX_VERTEX_NUM; i++)
	{
		for (int j = 0; j < _MAX_VERTEX_NUM; j++)
		{
			this->arcs[i][j].adj = 0;
			this->arcs[i][j].info = NULL;
		}
	}
	//Traversing Edge Data List
	for (int i = 0; i < arcsList->Length(); i++)
	{
		//Sequential acquisition of edges (arcs)
		arcData = arcsList->Get(i);
		//Locate (or set) the vertex positions at both ends of the edge
		m = _Locate(arcData->Tail);
		n = _Locate(arcData->Head);
		//Set vertex adjacent to 1 (directed)
		if (this->arcs[m][n].adj == 1 || this->arcs[n][m].adj == 1)
		{
			//Remove duplicate edges
			continue;
		}
		this->arcs[m][n].adj = 1;
		this->arcs[n][m].adj = 1;
		//Edge count
		this->arcNum++;
	}
}
 
void GraphAdjMat::_CreateDN(ObjArrayList<ArcData> * arcsList)
{
	/*
	.	Creating Directed Networks
	.	Vertex adjacency: infinity | non-adjacent w | adjacent
	.	Adjacency matrix is asymmetric matrix
	*/
	//Initialize temporary edge objects
	ArcData * arcData = NULL;
	//Initialization Matrix Two-Dimensional Coordinates
	int m = 0, n = 0;
	//Adjacency Matrix of Initialization Edge
	for (int i = 0; i < _MAX_VERTEX_NUM; i++)
	{
		for (int j = 0; j < _MAX_VERTEX_NUM; j++)
		{
			this->arcs[i][j].adj = this->_INFINITY;	//Infinity
			this->arcs[i][j].info = NULL;
		}
	}
	//Traversing Edge Data List
	for (int i = 0; i < arcsList->Length(); i++)
	{
		//Sequential acquisition of edges (arcs)
		arcData = arcsList->Get(i);
		//Locate (or set) the vertex positions at both ends of the edge
		m = _Locate(arcData->Tail);
		n = _Locate(arcData->Head);
		//Set vertex adjacent to weight weight
		if (this->arcs[m][n].adj != this->_INFINITY)
		{
			//Remove duplicate edges
			continue;
		}
		this->arcs[m][n].adj = arcData->Weight;
		//Edge count
		this->arcNum++;
	}
}
 
void GraphAdjMat::_CreateUDN(ObjArrayList<ArcData> * arcsList)
{
	/*
	.	Creating undirected network
	.	Vertex adjacency: infinity | non-adjacent w | adjacent
	.	Adjacency matrix is symmetric matrix
	*/
	//Initialize temporary edge objects
	ArcData * arcData = NULL;
	//Initialization Matrix Two-Dimensional Coordinates
	int m = 0, n = 0;
	//Adjacency Matrix of Initialization Edge
	for (int i = 0; i < _MAX_VERTEX_NUM; i++)
	{
		for (int j = 0; j < _MAX_VERTEX_NUM; j++)
		{
			this->arcs[i][j].adj = this->_INFINITY;	//Infinity
			this->arcs[i][j].info = NULL;
		}
	}
	//Traversing Edge Data List
	for (int i = 0; i < arcsList->Length(); i++)
	{
		//Sequential acquisition of edges (arcs)
		arcData = arcsList->Get(i);
		//Locate (or set) the vertex positions at both ends of the edge
		m = _Locate(arcData->Tail);
		n = _Locate(arcData->Head);
		//Set vertex adjacent to weight weight
		if (this->arcs[m][n].adj != this->_INFINITY || this->arcs[n][m].adj != this->_INFINITY)
		{
			//Remove duplicate edges
			continue;
		}
		if (arcData->Weight == this->_INFINITY)
		{
			//Remove edges with infinite weight
			continue;
		}
		this->arcs[m][n].adj = arcData->Weight;
		this->arcs[n][m].adj = arcData->Weight;
		//Edge count
		this->arcNum++;
	}
}
 
int GraphAdjMat::_Locate(string vertex)
{
	/*
	.	Location of vertex elements
	.		Later, it can be changed to a dictionary tree, and the location of vertices can be faster after the number of vertices exceeds 100.
	*/
	//Traversal locating vertex position
	for (int i = 0; i < this->_MAX_VERTEX_NUM; i++)
	{
		if (vertex == this->vexs[i])
		{
			return i;
		}
	}
	cout << endl << "vertex[" << vertex << "]Non-existent." << endl;
	return -1;
}
 
void GraphAdjMat::Display()
{
	/*
	.	Display Graph | Net (Output Vertex Array, Adjacency Matrix)
	*/
	//Display vertex array
	//Note: When an intermediate ordinal vertex is deleted, the vertex array is not continuous.
	cout << endl << "Vertex array:" << endl;
	for (int i = 0, num = 0; i < this->_MAX_VERTEX_NUM && num < this->vexNum; i++)
	{
		if (this->vexs[i] != "")
		{
			cout << " (" << i << ")" << this->vexs[i];
			num++;
		}
	}
	//Display edge (adjacency matrix)
	cout << endl << "Edge (adjacency matrix):" << endl;
	cout << "    ";
	for (int i = 0; i < this->_MAX_VERTEX_NUM; i++)
	{
		cout << "[" << i << "]";
	}
	cout << endl;
	for (int i = 0; i < this->_MAX_VERTEX_NUM; i++)
	{
		cout << "[" << i << "] ";
		for (int j = 0; j < this->_MAX_VERTEX_NUM; j++)
		{
			if (this->arcs[i][j].adj == this->_INFINITY)
				cout << " + ";
			else
				cout << " " << this->arcs[i][j].adj << " ";
		}
		cout << endl;
	}
}
 
void GraphAdjMat::InsertVertex(string *vertex)
{
	/*
	.	Insert a new vertex
	*/
	//1. Judging whether a vertex already exists
	if (_Locate(*vertex) > -1)
	{
		cout << endl << "The vertex already exists." << endl;
		return;
	}
	//2. Judging whether the number of vertices reaches the upper limit
	if (this->vexNum >= this->_MAX_VERTEX_NUM)
	{
		cout << endl << "The number of vertices has reached the upper limit." << endl;
		return;
	}
	//3. Insert new vertices and increase the total number of vertices
	int * index = vexs_null_index_queue->DeQueue();	//Retrieve from an empty location index queue
	this->vexs[*index] = *vertex;
	this->vexNum++;
	//4. Additional vertices do not require any operations in the adjacency matrix (initialized)
 
}
 
void GraphAdjMat::DeleteVertex(string *vertex)
{
	/*
	.	Delete a vertex
	*/
	//1. Judging whether a vertex already exists
	int index = _Locate(*vertex);
	if (index == -1)
	{
		cout << endl << "The vertex does not exist." << endl;
		return;
	}
	//2. Delete the vertex and reduce the total number of vertices
	this->vexs[index] = "";
	this->vexNum--;
	//3. Clear the data of the index row and column of the adjacency matrix and restore the initialization state of the row and column
	if (this->type == DG || this->type == UDG)
	{
		//chart
		for (int i = 0; i < this->_MAX_VERTEX_NUM; i++)
		{
			this->arcs[i][index].adj = 0;
			this->arcs[index][i].adj = 0;
		}
	}
	else
	{
		//network
		for (int i = 0; i < this->_MAX_VERTEX_NUM; i++)
		{
			this->arcs[i][index].adj = this->_INFINITY;
			this->arcs[index][i].adj = this->_INFINITY;
		}
	}
}
 
 
void GraphAdjMat::InsertArc(ArcData *arc)
{
	/*
	.	Insert a new edge (arc)
	.		If it already exists, it will be updated
	*/
	//1. Locating vertex position
	int i = _Locate(arc->Tail);
	int j = _Locate(arc->Head);
	//2. Judging whether a vertex exists
	if (i == -1 || j == -1)
	{
		cout << endl << "The edge vertex does not exist." << endl;
		return;
	}
	//3. Insert/update an edge
	if (this->type == DG)
	{
		//Directed Unweighted Graphs
		this->arcs[i][j].adj = 1;
	}
	else if (this->type == UDG)
	{
		//Undirected weightless graph
		this->arcs[i][j].adj = 1;
		this->arcs[j][i].adj = 1;
	}
	else if (this->type == DN)
	{
		//Directed Authority Network
		this->arcs[i][j].adj = arc->Weight;
	}
	else
	{
		//Undirected power network
		this->arcs[i][j].adj = arc->Weight;
		this->arcs[j][i].adj = arc->Weight;
	}
}
 
void GraphAdjMat::DeleteArc(ArcData *arc)
{
	/*
	.	Delete an edge (arc)
	*/
	//1. Locating vertex position
	int i = _Locate(arc->Tail);
	int j = _Locate(arc->Head);
	//2. Judging whether a vertex exists
	if (i == -1 || j == -1)
	{
		cout << endl << "The edge vertex does not exist." << endl;
		return;
	}
	//3. Delete an edge, that is, restore the initialization state
	if (this->type == DG)
	{
		//Directed Unweighted Graphs
		this->arcs[i][j].adj = 0;
	}
	else if (this->type == UDG)
	{
		//Undirected weightless graph
		this->arcs[i][j].adj = 0;
		this->arcs[j][i].adj = 0;
	}
	else if (this->type == DN)
	{
		//Directed Authority Network
		this->arcs[i][j].adj = this->_INFINITY;
	}
	else
	{
		//Undirected power network
		this->arcs[i][j].adj = this->_INFINITY;
		this->arcs[j][i].adj = this->_INFINITY;
	}
}
 
void GraphAdjMat::Display_DFS(string *vertex)
{
	/*
	.	Depth-first traversal display, starting at the specified vertex
	*/
	//1. Judging whether a vertex exists
	int index = _Locate(*vertex);
	if (index == -1)
		return;
	//2. Initialize Vertex Access Array
	for (int i = 0; i < this->_MAX_VERTEX_NUM; i++)
	{
		this->vexs_visited[i] = 0;
	}
	//3. Depth-first traversal recursion
	cout << "Depth-first traversal: (from vertices)" << *vertex << "Start)" << endl;
	_DFS_R(index);
}
 
void GraphAdjMat::_DFS_R(int index)
{
	/*
	.	Depth-first traversal recursion
	.		Directed/undirected algorithms are the same
	.		Directed graph | net, traversing in the direction of exit of the current vertex
	.		Undirected graph | net, traversing in the direction of the adjacent nodes of the current vertex (can be understood as "outgoing", but not outgoing)
	*/
	//1. Access vertices and mark accessed vertices
	cout << this->vexs[index] << " ";
	this->vexs_visited[index] = 1;
	//2. Access its adjacent vertices
	for (int i = 0; i < this->_MAX_VERTEX_NUM; i++)
	{
		//Accessible when the boundary value is not a non-adjacent int value (0 | weightless infinite | weighted) and has not been accessed out of date
		if (this->arcs[index][i].adj != this->nonAdjInt && this->vexs_visited[i] != 1)
		{
			_DFS_R(i);
		}
	}
}
 
void GraphAdjMat::Display_BFS(string *vertex)
{
	/*
	.	Breadth-first traversal display, starting at the specified vertex
	.		Tree-like hierarchical traversal algorithm
	*/
	//1. Judging whether a vertex exists
	int index = _Locate(*vertex);
	if (index == -1)
		return;
	//2. Initialize Vertex Access Array
	for (int i = 0; i < this->_MAX_VERTEX_NUM; i++)
	{
		this->vexs_visited[i] = 0;
	}
	//3. breadth-first traversal
	cout << "Breadth-first traversal: (from vertex)" << *vertex << "Start)" << endl;
	//3.1. Initialization queue
	LinkQueue<int> * vexQ = new LinkQueue<int>();
	//3.2. Visit the start vertex and mark access and entry
	cout << this->vexs[index] << " ";
	this->vexs_visited[index] = 1;
	vexQ->EnQueue(new int(index));
	//3.3. Get out of the team and traverse the adjacent vertices (next level), then join the team after visiting.
	while (vexQ->GetHead() != NULL)
	{
		index = *vexQ->DeQueue();
		for (int j = 0; j < _MAX_VERTEX_NUM; j++)
		{
			//Unvisited adjacent vertices
			if (this->arcs[index][j].adj != this->nonAdjInt && this->vexs_visited[j] != 1)
			{
				//Visit the vertex and mark access and queue entry
				cout << this->vexs[j] << " ";
				this->vexs_visited[j] = 1;
				vexQ->EnQueue(new int(j));
			}
		}
	}
 
	//4. Release queue
	int * e;
	while (vexQ->GetHead() != NULL)
	{
		e = vexQ->DeQueue();
		delete e;
	}
	delete vexQ;
}

//File name: "GraphAdjMat_Test.cpp"
#include "stdafx.h"
#include <iostream>
#include "GraphAdjMat.h"
#include "ObjArrayList.h"
using namespace std;
 
int main()
{
	//Initialize vertex data
	string * v1 = new string("v1");
	string * v2 = new string("v2");
	string * v3 = new string("v3");
	string * v4 = new string("v4");
	string * v5 = new string("v5");
	string * v6 = new string("v6");
	string * v7 = new string("v7");
	ObjArrayList<string> * vexs = new ObjArrayList<string>();
	vexs->Add(v1);
	vexs->Add(v2);
	vexs->Add(v3);
	vexs->Add(v4);
	vexs->Add(v5);
	vexs->Add(v6);
	vexs->Add(v7);
 
	//Initialize edge (arc) data
	GraphAdjMat::ArcData * arc1 = new GraphAdjMat::ArcData{ "v1", "v2", 2 };
	GraphAdjMat::ArcData * arc2 = new GraphAdjMat::ArcData{ "v1", "v3", 3 };
	GraphAdjMat::ArcData * arc3 = new GraphAdjMat::ArcData{ "v1", "v4", 4 };
	GraphAdjMat::ArcData * arc4 = new GraphAdjMat::ArcData{ "v3", "v1", 5 };
	GraphAdjMat::ArcData * arc5 = new GraphAdjMat::ArcData{ "v3", "v2", 6 };
	GraphAdjMat::ArcData * arc6 = new GraphAdjMat::ArcData{ "v3", "v5", 7 };
	GraphAdjMat::ArcData * arc7 = new GraphAdjMat::ArcData{ "v2", "v5", 8 };
	GraphAdjMat::ArcData * arc8 = new GraphAdjMat::ArcData{ "v4", "v6", 9 };
	GraphAdjMat::ArcData * arc9 = new GraphAdjMat::ArcData{ "v4", "v7", 9 };
	GraphAdjMat::ArcData * arc10 = new GraphAdjMat::ArcData{ "v6", "v7", 9 };
	ObjArrayList<GraphAdjMat::ArcData> * arcsList = new ObjArrayList<GraphAdjMat::ArcData>();
	arcsList->Add(arc1);
	arcsList->Add(arc2);
	arcsList->Add(arc3);
	arcsList->Add(arc4);
	arcsList->Add(arc5);
	arcsList->Add(arc6);
	arcsList->Add(arc7);
	arcsList->Add(arc8);
	arcsList->Add(arc9);
	arcsList->Add(arc10);
 
	//Test 1: undirected graph
	cout << endl << "Undirected graph initialization:" << endl;
	GraphAdjMat * udg = new GraphAdjMat(GraphAdjMat::UDG);
	udg->Init(vexs, arcsList);
	udg->Display();
	//1.1. Depth-first traversal
	cout << endl << "Depth-first traversal sequence of undirected graph:" << endl;
	udg->Display_DFS(v1);
	//1.2. breadth-first traversal
	cout << endl << "The breadth-first traversal sequence of undirected graphs:" << endl;
	udg->Display_BFS(v2);
	//1.3. Insert new vertices and edges
	cout << endl << "New vertices and edges are inserted into undirected graphs:" << endl;
	udg->InsertVertex(new string("v8"));
	udg->InsertArc(new GraphAdjMat::ArcData{ "v8", "v1", 8 });
	udg->Display();
	//1.4. Delete vertices and edges
	cout << endl << "Delete vertices from undirected graphs v1,edge arc9: " << endl;
	udg->DeleteVertex(v1);
	udg->DeleteArc(arc9);
	udg->Display();
 
	//Test 2: Directed graph
	cout << endl << "Digraph:" << endl;
	GraphAdjMat * dg = new GraphAdjMat(GraphAdjMat::DG);
	dg->Init(vexs, arcsList);
	dg->Display();
	//2.1. Depth-first traversal
	cout << endl << "Directed graph depth-first traversal sequence:" << endl;
	dg->Display_DFS(v1);
	//2.2. breadth-first traversal
	cout << endl << "Directed graph breadth-first traversal sequence:" << endl;
	dg->Display_BFS(v2);
 
	//Testing: undirected network
	cout << endl << "Undirected network:" << endl;
	GraphAdjMat * udn = new GraphAdjMat(GraphAdjMat::UDN);
	udn->Init(vexs, arcsList);
	udn->Display();
 
	//Test: Directed Network
	cout << endl << "Directed network:" << endl;
	GraphAdjMat * dn = new GraphAdjMat(GraphAdjMat::DN);
	dn->Init(vexs, arcsList);
	dn->Display();
	
	return 0;
}