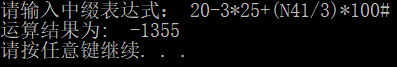Title Requirements

Enter the infix expression from the keyboard, set up the stack of operands and operators, and calculate and output the evaluation results of the expression.
Basic requirements: implement +, -, *, /four binary operators and (); operands range from 0 to 9.
Increased requirements: implement +, - two unary operators (i.e., positive and negative signs); operands can be any integer value (program does not consider calculation overflow).
If two integers are divided, only the integer quotient is preserved (the remainder is discarded); expression syntax errors are not handled.

Involving knowledge points

Stack and Queue

Data structure design

A C++ template class is used to create Operator Stack OPND with integer element type and Operator Stack OPTR with character type. In each stack object, the elem pointer is used to create an array of length n, n is the maximum number of elements in the stack, and top is the top pointer.

Algorithmic Description

1. The infix expression ends with'#', and the'#'character is also used as an operator.
(2)'(','))'is treated as an operator and parentheses need to be removed after the operation in parentheses is completed.
(3) Two different types of stacks need to be built, the integer operand stack OPND and the character operator stack OPTR.
(4) The main steps of the algorithm:
a. Initially, OPND is empty with'#'as the bottom element of the OPTR stack;
b. Read each character in the expression in turn, and if an operand, press directly into the OPND stack;
c. If the operator (denoted as theta), the top operator of the PTR stack (denoted as lambda) takes precedence;
Lambda <theta, theta pushes into the OPTR stack and continues reading the next character;
Lambda=theta, parentheses off, continue reading the next character;
Lambda>theta, performs the lambda operation (lambda de-stacking), theta equals outside the stack (do not read the next character), that is, theta continues to be preferred to the OPTR top operator (repeat the above operation) until theta can be stacked.
For unary operators (positive and negative signs), use'P'for'+','N' for'-'.

Program Code

#include<iostream>
using namespace std;
template <typename T>
class Stack                 //Template class: stack
{
public:
    Stack();                //Default constructor
    Stack(int n);           //Constructor that calls the function createStack(int n) to create a stack of length n
    ~Stack();               //Fictitious function
    int createStack(int n); //Create a stack of length n
    int empty();            //Determine if stack is empty
    int full();             //Determine if the stack is full
    int push(T e);          //Stack element e
    int pop(T &e);          //Element out of stack, saved in e
    T get_top();            //Get the top element of the stack
    friend int isoperator(char &e);//Determine whether character e is an operator
    friend int isp(char &e);//Returns the priority of an operator on the stack
    friend int icp(char &e);//Returns the priority of an out-of-stack operator
    friend int compute(int x, char a, int y);//Evaluation function
private:
    T *elem;                //Create an array of length n
    int n;                  //Maximum number of elements in stack
    int top;                //top of stack
};
template<typename T>
Stack<T>::Stack()
{
    top = -1;
}
template<typename T>
Stack<T>::Stack(int n)
{
    createStack(n);
}
template<typename T>
Stack<T>::~Stack()
{
    n = 0;
    top = -1;
    delete[]elem;
}
template<typename T>
int Stack<T>::createStack(int n)
{
    if (n <= 0)
        return 0;
    this->n = n;
    top = -1;
    elem = new T[n];
    if (!elem)
        return 0;
    return 1;
}
template<typename T>
int Stack<T>::empty()
{
    return top == -1;
}
template<typename T>
int Stack<T>::full()
{
    return top >= n - 1;
}
template<typename T>
int Stack<T>::push(T e)
{
    if (top >= n - 1)
        return 0;
    elem[++top] = e;
    return 1;
}
template<typename T>
int Stack<T>::pop(T & e)
{
    if (top == -1)
        return 0;
    e = elem[top--];
    return 1;
}
template<typename T>
T Stack<T>::get_top()
{
    return elem[top];
};
int isoperator(char &e)        //Determine whether it is an operator
{
    if (e == '+' || e == '-' || e == '*' || e == '/' || e == '(' || e == ')' || e == '#' || e == 'P' || e == 'N')
        return 1;      //Is operator returns 1
    else
        return 0;      //Not an operator returns 0
}
int isp(char &e)               //Returns the priority of an operator on the stack
{
    switch (e)
    {
    case '#':
        return 0; break;
    case '(':
        return 1; break;
    case '+':
    case '-':
        return 2; break;
    case '*':
    case '/':
        return 3; break;
    case 'P':
    case 'N':
        return 4; break;
    case ')':
        return 5; break;
    default:
        return -1; break;
    }
}
int icp(char &e)                 //Returns the priority of an out-of-stack operator
{
    switch (e)
    {
    case '#':
        return 0; break;
    case ')':
        return 1; break;
    case '+':
    case '-':
        return 2; break;
    case '*':
    case '/':
        return 3; break;
    case 'P':
    case 'N':
        return 4; break;
    case '(':
        return 5; break;
    default:
        return -1; break;
    }
}
int compute(int x, char a, int y)
{
    switch (a)
    {
    case '+':                //Calculate Addition
        return x + y; break;
    case '-':                //Calculate Subtraction
        return x - y; break;
    case '*':                //Calculate Multiplication
        return x * y; break;
    case '/':                //Calculate Division
        return x / y; break;
    default:
        return -1; break;
    }
}
int g1()
{
    char a, b, c;
    int i, j, f, value, firstOpnd, secondOpnd, m;
    Stack<char> OPTR(MAX);    //Build Operator Stack
    Stack<int> OPND(MAX);     //Build Operand Stack
    OPTR.push('#');           //'#'Stack
    cout << "Please enter an infix expression: ";
    a = getchar();
    while (a != '#' || OPTR.get_top() != '#')
    {
        if (!isoperator(a))   //Not an operator, that is an operand, operands stacked
            OPND.push(a - 48);//Converting Character Types to Integer Numbers
        else                  //Is an operator that compares the priority size to the top stack operator
        {
            b = OPTR.get_top();//Get the top element of the stack
            i = isp(b);       //Priority of stack top operator
            j = icp(a);       //Priority of off-stack operators
            if (i < j)        //Out-of-stack operators have high priority and operators are stacked
                OPTR.push(a);
            else
            {
                OPTR.pop(b);                    
                if (b != '('&&i == j || i > j)
                {
                    c = OPTR.get_top();
                    if ((c == '(' || c == '#') & && (b =='P'|| B =='N') /*c is unary
                                                                            Operator: Positive and negative sign*/
                    {
                        OPND.pop(firstOpnd); //Get Operand
                        switch (b)
                        {
                        case 'P':            //Positive sign
                            f = firstOpnd * 1;
                            break;
                        case 'N':            //Minus sign
                            f = firstOpnd * (-1);
                            break;
                        }
                    }
                    else                     //c is a binary operator
                    {
                        OPND.pop(secondOpnd); //Get the second operand
                        OPND.pop(firstOpnd);  //Get the first operand
                        f = compute(firstOpnd, b, secondOpnd); //Calculate Evaluation
                    }
                    OPND.push(f);             //Evaluation Result Stack
                    continue;
                }
            }
        }
        c = a;
        a = getchar();                         //Continue reading characters
        while(!isoperator(a) && !isoperator(c))  /*Multiply the bit weight if the continuous read characters are all numbers
                                                  Get multidigits*/
        {
            OPND.pop(m);
            m = m * 10 + a - 48;
            OPND.push(m);
            c = a;
            a = getchar();
        }
        
    }
    OPND.pop(value);
    return value;      //Returns the result of an expression
}
int main()
{
    int a;
    a = g1();
    cout << "The result of the operation is:  " << a << endl;
    return 0;
}

Example

(1) Program input: 3+5* (9-5)/10#
Program Output: 5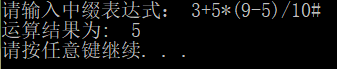

(2) Program input: P9+10*(N2*8/4)-10#
Program Output: -41

(3) Program input: 20-3*25+(N41/3)*100#
Program Output: -1355