1, Basic concept of graph

 

Graph - graph G is composed of two sets V(G) and E(G), marked as G=(V,E), where V(G) is a non empty finite set of vertices,   E(G) is a finite set of edges, and edges are disordered or ordered pairs of vertices.

Graph cannot be empty

1. Terms and definitions of drawings

1) Directed graph

If E is a finite set of directed edges, then graph G is a directed graph. An arc is a directed pair of vertices, which is recorded as < V, w >, where V, w ∈ V, V is called the arc tail, W is called the arc head, and < V, w > is called the arc from V to W

2) Undirected graph

If E is a finite set of undirected edges, then graph G is an undirected graph. Edges are undirected pairs of vertices, denoted as (V, w) or (W, v), where V, w ∈ v

3) Simple graph

A graph G is called a simple graph if it satisfies that there are no repeated edges and rings.

4) Complete graph

A graph with edges between each vertex. Undirected complete graphs have n(n-1)/2 edges, and directed complete graphs have n(n-1) arcs

5) Subgraph

There are two graphs G1=(V1,E1) and G2(V2,E2). If V2 is a subset of V1 and E2 is a subset of E1, G2 is said to be a subgraph of G1. If V2=V1, G2 is said to be the generated subgraph of G1.

6) Connected, connected graph, connected component

In an undirected graph, if there is a path from vertex v to vertex w, then V and w are connected. If any two vertices in graph G are connected, graph G is called connected graph. A polar connected subgraph in an undirected graph is called a connected component. If the graph is unconnected, there can be at most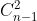Strip edge

7) Strongly connected graph, strongly connected component

In a directed graph, if a pair of vertices v and w have paths from v to W and from w to v, the two vertices are said to be strongly connected. If any pair of vertices in a graph are strongly connected, the graph is called strongly connected. The maximal strongly connected subgraphs in a directed graph are called the strongly connected classification of a directed graph.

8) Spanning tree

The spanning tree of a connected graph is a minimal connected subgraph containing all vertices in the graph. If the number of vertices in the graph is n, its spanning tree contains n-1 edges.

In a non connected graph, the spanning tree of connected components constitutes the spanning forest of a non connected graph.

9) Vertex degrees, in degrees and out degrees

In an undirected graph, the degree of vertex v refers to the number of edges attached to vertex v, which is recorded as TD(v). For an undirected graph with n vertices and e edges, the sum of degrees is twice the number of edges.

In a directed graph, the degree of vertex v is divided into in degree and out degree. In degree is the number of arcs ending at vertex v, which is recorded as ID(v); Out degree is the number of directed edges starting from vertex v, which is recorded as OD(v).

10) Edge weight and net

In a graph, each edge can be marked with a value with some meaning, which is called the weight of the edge. This kind of graph with weight on the edge is called weighted graph, also known as net.

11) Dense graph

A graph with few edges is called a sparse graph, and vice versa is called a dense graph. Generally, when graph G satisfies | e | < | V | log | V |, G can be regarded as a sparse graph.

12) Path, path length and loop

A path from vertex Vp to Vq refers to the vertex sequence Vp, Vi1, Vi2,..., Vim, Vq. The number of edges on the path is called the path length. The same path between the first vertex and the last vertex is called a loop or ring. If a graph has n vertices and more than n-1 edges, the graph must have a ring.

13) Simple path

In the path sequence, the path where the vertices do not appear repeatedly is called a simple path. Except for the first vertex and the last vertex, the circuit in which other vertices do not reappear is called a simple circuit.

14) Distance

If the shortest path from vertex u to vertex v exists, the length of this path is called the distance from u to v

15) Directed tree

A directed graph in which the penetration of one vertex is 0 and the penetration of other vertices is 1 is called a directed tree.

16) Euler chart

The loop (back to the starting point) that passes through all vertices of each edge of the graph once and only once is called Euler loop, and the graph with Euler loop is called Euler graph.

17) Hamiltonian graph

A circuit that passes through all vertices of a graph only once is called a Hamiltonian circuit. This kind of graph is called a Hamiltonian graph.

2. Storage of drawings

1) Adjacency matrix method

A one-dimensional array is used to store the vertex information in the graph, and a two-dimensional array is used to store the edge information in the graph. The two-dimensional array that stores the adjacency relationship between vertices is called adjacency matrix.

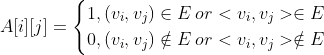
#define MaxVertexNum 100
typedef struct{
    char Vex[MaxVertexNum];
    int Edge[MaxVertexNum][MaxVertexNum];
    int vexnum,arcnum;
}MGraph;

Required storage space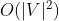

The adjacency matrix of an undirected graph must be symmetric and unique, so only the upper (lower) triangle needs to be stored in the actual storage

For an undirected graph, the number of non-zero elements in row i of the adjacency matrix is exactly the degree of vertex i

For a directed graph, the number of non-zero elements in row I of the adjacency matrix is the out degree of vertex i, and the number of non-zero elements in column I is the in degree of vertex I  

Fit dense graph

Let the adjacency matrix of graph G be A,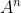The non-zero element of is equal to the number of paths with length n from vertex i to vertex j.

2) Adjacency table method

A single linked list is established for each vertex of graph G, and the nodes in the single linked list represent the edges attached to vertex vi

typedef struct edge_node
{
	int adjvex;
	struct edge_node *next;
}edge;
typedef struct vertex_node
{
	char data;
	edge *first_edge;
}vertex;
typedef struct
{
	vertex adjlist[1000];
	int numVertex;
	int numEdge;
}GraphAdjList;

The storage space of undirected graph is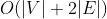, the storage space of digraph is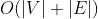

Suitable for sparse graph

3) Cross linked list

In the adjacency table of a directed graph, to find the penetration of a point, you need to traverse the whole edge set, use a cross linked list, and increase the head field to connect the edges with the same arc head.

typedef  struct  ArcBox
{   int   tailvex,  headvex;   // Position of arc tail and arc head in header array
     struct   arcnode   *hlink；  // Point to the next arc with the same arc head
     struct   arcnode   *tlink;      // Point to the next arc with the same tail
} ArcBox;
typedef  struct  VexNode
{  VertexType   data; // Save information about vertices
    ArcBox *firstin；  // Point to the first arc node with this vertex as the arc head
    ArcBox *firstout;  // Point to the first arc node with this vertex as the arc tail
} VexNode;
VexNode  OLGraph[M];

4) Adjacency multiple table

In the adjacency table of undirected graph, the same edge is stored twice, and the adjacency multiple table is used to increase jlink to point to the next edge attached to vertex j.

typedef   struct  node
{   VisitIf  mark;   // Flag field, whether the record has been searched
     int  ivex, jvex;  // The two vertices attached to the edge are located in the header array
     struct  EBox   * ilink,  * jlink;  
//Point to the next edge attached to ivex and jvex, respectively
} EBox;
ypedef   struct  VexBox
{    VertexType   data;              // Save information about vertices
      EBox  * firstedge;              // Points to the first edge attached to the vertex
} VexBox;
VexBox  AMLGraph[M];

3. Graph traversal

1) Breadth first search BFS

Idea: first access the starting vertex v, then start from V, access each unreachable vertex w1, w2,..., wi of V in turn, and then access all unreachable adjacent vertices of w1, w2,..., WI in turn. Repeat the above process until all vertices have been accessed. If there are still inaccessible vertices in the graph, select another inaccessible vertex as the starting point.

bool visited[MaxVertexNum];
void BFSTraverse(Graph G) {
	for (int i = 0; i < G.vexnum; i++) visited[i] = false;
	InitQueue(Q);
	for (int i = 0; i < G.vexnum; i++) {
		if (!visited[i]) BFS(G, i);
	}
}
void BFS(Graph G, int v) {
	visit(v);
	visited[v] = true;
	EnQueue(Q, v);
	while (!IsEmpty(Q)) {
		DeQueue(Q, v);
		for (w = FirstNeighbour(G, v); w >= 0; w = NextNeighbour(G, v, w)) {
			if (!visited[w]) {
				visit(w);
				visited[w] = true;
				EnQueue(Q, w);
			}
		}
	}
}

Spatial complexity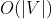

When using adjacency table storage, each vertex needs to be searched once. When searching the temporary contact of any vertex, each edge is accessed at least once, and the time complexity is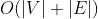

When using adjacency matrix storage, the time complexity is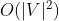

  2) Depth first search

First access the starting vertex v, then start from V to access any vertex w1 adjacent to V and not accessed, and then access any vertex w2 adjacent to w1 and not accessed, and repeat the above process. When the downward access can no longer be continued, it will return to the recently accessed vertex in turn. If it has adjacent vertices that have not been accessed, it will continue the above search process from this point until all vertices are accessed.

bool visited[MaxVertexNum];
void DFSTraverse(Graph G) {
	for (int i = 0; i < G.vexnum; i++) visited[i] = false;
	for (int i = 0; i < G.vexnum; i++) {
		if (!visited[i]) DFS(G, i);
	}
}
void DFS(Graph G, int v) {
	visit(v);
	visited[v] = true;
	EnQueue(Q, v);
	while (!IsEmpty(Q)) {
		DeQueue(Q, v);
		for (w = FirstNeighbour(G, v); w >= 0; w = NextNeighbour(G, v, w)) {
			if (!visited[w]) {
				DFS(G, w);
			}
		}
	}
}

Spatial complexity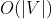

When using adjacency table storage, each vertex needs to be searched once. When searching the temporary contact of any vertex, each edge is accessed at least once, and the time complexity is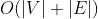

When using adjacency matrix storage, the time complexity is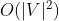

3) Connectivity of Graphs

For an undirected graph, if the undirected graph is connected, all vertices in the graph can be accessed only once from any node; If it is not connected, starting from a vertex, one traversal can only access all vertices of the connected component of the vertex. For a directed graph, if there is a path from the initial vertex to each vertex in the graph, all vertices in the graph can be accessed.

2, Application of graph

1. Minimum spanning tree (minimum connected subgraph, including all vertices and n-1 edges)

If a communication network is to be established between n cities, only n-1 lines need to be built to connect n cities. How to establish this communication network on the premise of saving the most money?

1) Prim algorithm

Let G=(V, GE) be a connected network with n vertices, and T=(U, TE) be a spanning tree.

(1) Initially, U = {u0}, TE = {};         

(2) At all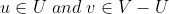Select one of the edges (u,v) with the smallest weight, which may be set to (u,v);         

(3) (u,v) add TE and add v to u;         

(4) Repeat (2) (3) until U=V;

void MiniSpanTree_P(MGraph G, VertexType u)
{
	//Using prim algorithm to construct the minimum spanning tree of network G from vertex u
	k = LocateVex(G, u);
	for (j = 0; j < G.vexnum; ++j)  // Auxiliary array initialization
		if (j != k)
			closedge[j] = { u, G.arcs[k][j] };
	closedge[k].Lowcost = 0;      // Initial, u = {u}
	for (i = 1; i < G.vexnum; ++i)
	{
		k = minimum(closedge);
		// Find the next vertex (k) added to the spanning tree
		printf(closedge[k].Adjvex, G.vexs[k]);
		// Outputs an edge on the spanning tree
		closedge[k].Lowcost = 0; // The k-th vertex is merged into the U set
		for (j = 0; j < G.vexnum; ++j)
			// Modify the smallest edge of other vertices
			if (G.arcs[k][j] < closedge[j].Lowcost)
				closedge[j] = { G.vexs[k], G.arcs[k][j] };
	}
}

The time complexity of Prim algorithm is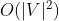, independent of | E |, it is suitable for solving the minimum spanning tree of edge dense graphs.

2) Kruskal algorithm

Let the connected network N = (V, {e}).

① Initially, the minimum spanning tree contains only n vertices of the graph, and each vertex is a subtree (forming a connected component);

② Select the edge whose weight is small and the associated two vertices are not in the same connected component, and add this edge to the minimum spanning tree;

③ Repeat ② n-1 times to obtain the minimum spanning tree containing n vertices and N-1 edges.

When Kruskal algorithm uses heap to store the set of edges, the time complexity is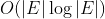Therefore, Kruskal algorithm is suitable for graphs with sparse edges and many vertices.

2. Shortest path

1) For unauthorized graphs, you can use breadth first search to find the shortest path

2) Dijkstra algorithm

Auxiliary set S: at the beginning of the vertex set for which the shortest path has been obtained, S={V0}

The auxiliary array Dist Dist[k] represents the shortest path from the source point to vertex K obtained by "current"

Dist [k] = < weight on arc from source point to vertex k > or = path len gt h along the "current" shortest path to vertex K

Assuming that the "current" shortest path is the path from the source point to vertex j, Dist[k] = "current" shortest path len gt h + < weight on the arc from vertex j to vertex k >

① Initialize S={v0}

There is an arc between V0 and K: Dist[k] = G.arcs[v0][k]

There is no arc between V0 and K: Dist[k] = infinite

②   Among all arcs starting from the source point, select an arc with the smallest weight, that is, the first shortest path.

③ Modify the Dist[k] values of other vertices whose shortest path has not been determined in turn.

Assuming that the vertex of the shortest path is u, Dist[k] = min (Dist[k], dist [u] + g.arcs [u] [k])

Repeat ② ③ n-1 times until all vertices are in S

#define MaxVertexNum 100
#define MAXN 0xffff    
typedef struct {
	char Vex[MaxVertexNum];
	int Edge[MaxVertexNum][MaxVertexNum];
	int vexnum, arcnum;
}MGraph;
void Dijkstra(MGraph M, int dist[]) {
	int visited[MaxVertexNum];
	for (int i = 0; i < M.vexnum; i++) {
		visited[i] = 0;
	}
	int flag = 0;
	while (flag != M.vexnum) {
		int d = MAXN;
		int v = -1;
		for (int i = 0; i < M.vexnum; i++) {
			if (dist[i] < d&&visited[i] == 0) {
				d = dist[i];
				v = i;
			}
		}
		if (d == MAXN) {
			break;
		}
		visited[v] = 1;
		flag++;
		for (int i = 0; i < M.vexnum; i++) {
			if (visited[i] == 0 && dist[v] + M.Edge[v][i] < dist[i]) {
				dist[i] = dist[v] + M.Edge[v][i];
			}
		}
	}
}
int main()
{
	MGraph M;
	int x, y, dis;
	char a, b, c;
	scanf("%d,%d,%c", &M.vexnum, &M.arcnum, &c);
	getchar();					//Read newline
	for (int i = 0; i < M.vexnum; i++)//initialization
	{
		for (int j = 0; j < M.vexnum; j++)
		{
			M.Edge[i][j] = (i == j) ? 0 : MAXN;
		}
	}
	for (int i = 0; i < M.arcnum; i++)
	{
		scanf("<%c,%c,%d>", &a, &b, &dis);
		getchar();
		x = a - 'a';//Convert characters into numbers
		y = b - 'a';
		if (M.Edge[x][y] > dis)
			M.Edge[x][y] = dis;
	}
	int num = c - 'a';
	int dist[MaxVertexNum];
	for (int i = 0; i < M.vexnum; i++) {
		dist[i] = M.Edge[num][i];
	}
	Dijkstra(M,dist);
	for (int i = 0; i < M.vexnum; i++)
	{
		printf("%c:%d\n", i + 'a', dist[i]);//Remember to turn back the character
	}
	//system("pause");
	return 0;
}

Time complexity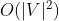

  It is worth noting that Dijkstra algorithm is not applicable when the edge has negative weight.

3) Floyd algorithm for the shortest path between vertices

According to the vertex sequence number, it is assumed that the shortest path with the maximum sequence number of intermediate nodes of any two vertices is K-1. On this basis, the shortest path with the maximum sequence number of intermediate nodes of any two vertices is further calculated.

① Initially, set an n-order square matrix so that its diagonal element is 0. If there is an arc < VI, VJ >, the corresponding element is the weight; Otherwise ∞.

② Gradually try to add intermediate vertices to the original direct path. If the path becomes shorter after adding intermediate vertices, modify it; Otherwise, maintain the original value.

③ All vertex probes are completed and the algorithm ends.

 

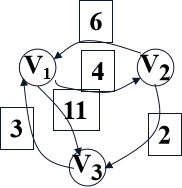
  Join V1 point investigation:

<v2, v3> = 2 ,<v2, v1> <v1,v3> = 17

<v3, v2> = ∞,<v3, v1> <v1,v2> = 7

 

  Join V2 point investigation:

<v1, v3> = 11             <v1, v2> <v2, v3> = 6            

<v3, v1> = 3             <v3, v2> <v2, v1> = 13

  Join V3 to investigate:

<v1, v2> = 4             <v1, v3> <v3, v2> = 13            

<v2, v1> = 6             <v2, v3> <v3, v1> = 5

3. Directed acyclic graph

If there is no ring in a directed graph, it is called directed acyclic graph, or DAG graph for short

Directed acyclic graph is an effective tool to describe expressions with common subexpressions. (the common subexpression is deleted in the code optimization part of compilation principle)

Input: a basic block Bi  

Output: DAG of basic block Bi containing the following information:        

(1) Leaf nodes and internal nodes are marked uniformly;        

(2) Each node has an identifier table (can be empty);  

Algorithm:      

Perform the following steps for each quaternion in the basic block

one   Construct leaf nodes;

two   Capture known quantities and merge constants// Delete original constant node

three   Capture common subexpressions;         // Remove redundant common subexpressions

four   Capture possible useless assignments;     // delete

4. Topology sorting

AOV network: if a DAG diagram is used to represent a project, vertices are used to represent activities, and arcs are used to represent the priority relationship between activities, it is called Activity On Vertex network (AOV network for short). Loops are not allowed in the AOV network, because loops mean that an activity takes itself (or successor) as a prerequisite.

Topological sorting: the process of arranging the vertices in the AOV network into a linear sequence according to their priority relationship.       

Method for detecting whether there are rings in AOV network: construct a topological ordered sequence of vertices for a directed graph. If all vertices in the network are in its topological ordered sequence, there must be no rings in the AOV network.

Select a vertex without a precursor in a directed graph and output it.

Delete the vertex and all arcs ending in it from the graph.         

Repeat the above two steps until all vertices have been output; Or when there is no Vertex without precursor in the graph.

int topo_sort(GraphAdjList *map)
{
	//Add points with a penetration of 0 to the queue
	for (int i = 0; i < map->numVertex; i++)
	{
		if (map->adjlist[i].index == 0)
		{
			queeu[rear] = i;
			rear++;
		}
	}
	int count = 0;
	while (1)
	{
		edge *p = map->adjlist[queeu[front]].first_edge;
		front++;		//One team at a time
		while (p != NULL)		//After leaving the team, the point penetration of the corresponding edge is reduced by one to judge whether the penetration is 0 and join if it is 0
		{
			map->adjlist[p->adjvex].index--;
			if (map->adjlist[p->adjvex].index == 0)
			{
				queeu[rear] = p->adjvex;
				rear++;
			}
			p = p->next;
		}
		QuickSort(front, rear - 1);	//sort
		if (rear == front)
		{
			break;
		}
		count++;	//Count the number of output vertices
	}
	if (count < map->numVertex - 1)		//If count > num, there must be a ring
	{
		return 0;
	}
	return 1;
}

5. Critical path

AOE net: the active net is represented by edges. It is a weighted directed acyclic graph. Vertices represent events / States, arcs represent activities, and weights represent the duration of activities. The path length represents the sum of the duration of each activity on the path, and the critical path represents the path with the longest path length.

Algorithm:

Calculate the earliest occurrence time ve(j) of "state (vertex)" and the latest occurrence time vl(k) of "state (vertex)"

Calculate the earliest start time e(i) of activity (ARC) and the latest start time l(i) of activity (ARC)

Key activities: e(i)  ＝ l(i)

Earliest start time: ve (source point) = 0; ve(k) = Max{ve(j) + dut(<j, k>)}

Latest start time: VL (sink) = ve (sink); vl(j) = Min{vl(k) – dut(<j, k>)}

The formula for calculating the occurrence time of activity (ARC) assumes that the i-th arc is < J, k >, then it is applicable to the i-th activity

e(i) = ve(j)； l(i) = vl(k) – dut(<j,k>)；

Find the ve of vertices according to the order of AOE network topology sequence; Find the vl of vertices in the order of inverse topological sequence; e[k] and l[k] of each activity are calculated by ve and vl; Find out the key activities of e[k]==l[k]

6. Connected component

BFS or DFS

7. Postman problem*

(1) If it is an Euler graph, the Euler loop is the shortest delivery route

(2) Otherwise, there are even odd vertices in the graph, so you only need to repeat the shortest path between each pair of odd vertices.

8.TSP issues*