Tip: after the article is written, the directory can be generated automatically. Please refer to the help document on the right for how to generate it

preface

In the last data structure column, we introduced the interface functions of the single linked list. You may find that the single linked list has some defects: for example, one node needs to store data + the address of the next node, which takes up much more space than the sequential table; And because the single linked list cannot be found from the back to the front, if you want to delete the tail, you must look back from the first node. Your time complexity must be O (n). In order to solve some of the above defects, let's introduce the two-way circular linked list today

Tip: the following is the main content of this article. The following cases can be used for reference

1, What is a circular two-way linked list

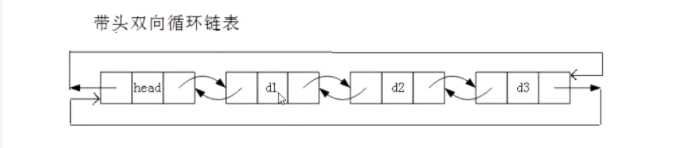
This linked list will have a sentinel head node pointing to d1, and then d1 pointing to d2... This is very similar to a single linked list.
But the biggest difference from a single linked list is that each node of this linked list will store not only the address of the next node, but also the address of the previous node, and then the tail node will store an address pointing to the sentinel bit head, and then the sentinel bit head will store an address pointing to the tail node.
The specific codes are as follows:

typedef int LTDataType;//If you need to change the linked list data type in the future, you can directly change it here (int)
typedef struct ListNode
{
	struct ListNode*next;
	struct ListNode*prev;
	LTDataType data;
}ListNode;//Structure weight naming

Example: pandas is a NumPy based tool created to solve data analysis tasks.

2, Linked list initialization

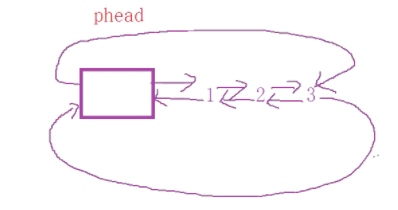
Similar to the effect shown in the figure above, only one node is created at the beginning, and its stored front address and rear address point to itself

The code is as follows (example):

#Include < stdlib. H > / / malloc function header file
ListNode* BuyListNode(LTDataType x)//Create a node
{
	ListNode*newnode = (ListNode*)malloc(sizeof(ListNode));
	newnode->data = x;
	newnode->next = NULL;
	newnode->prev = NULL;
	return newnode;
}
ListNode* ListInit()//Linked list initialization
{
	ListNode*phead = BuyListNode(0);
	phead->next = phead;
	phead->prev = phead;
	return phead;
}

ps: here, the ListInit function uses the method of return value. You can also use the secondary pointer to pass parameters for initialization

3, Linked list interface function

1. Tail plug

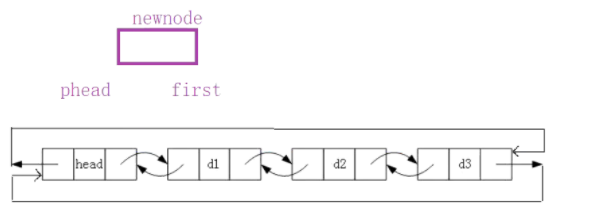
Let's take the above figure as an example. The predecessor of the head node of the original linked list points to 3, and then the follower of 3 points to the head node. How to perform tail interpolation after 3? Since the address of node 3 is stored in the head node, we can directly find node 3. What should we do after finding it? Change the precursor of the head node to the 4-node address, the 3-node driver to the 4-node address, and the last 4-node driver points to the head node. As shown below:

The code is as follows (example):

#Include < assert. H > / / assert function header file
void ListPushBack(ListNode*phead, LTDataType x)//Tail insertion
{
    assert(phead);//Assert the passed pointer, because you have to have at least one header node to tail insert
    //If a null pointer is passed, an error will be reported
	ListNode*tail = phead->prev;
	ListNode*newnode = BuyListNode(x);
	tail->next = newnode;
	newnode->prev = tail;
	newnode->data = phead;
	phead->prev = newnode;
}

2. Head insert

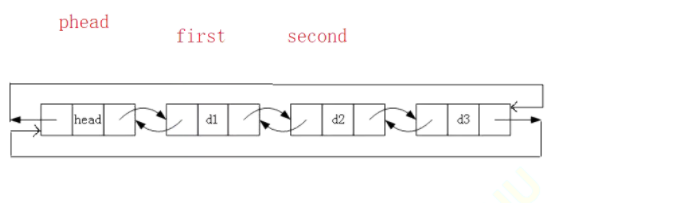
As shown in the figure above, first insert the head between head and d1. How to operate? Very simple, as like as two peas.
The rear driver of head points to newnode, the front and rear drivers of newnode point to phead and d1 respectively, and the front driver of d1 points to newnode, as shown in the figure below:

The code is as follows (example):

void ListPushFront(ListNode*phead,LTDataType x)
{
	assert(phead);
	ListNode*first = phead->next;
	ListNode*newnode = BuyListNode(x);
	phead->next = newnode;
	newnode->prev = phead;
	newnode->next = first;
	first->prev = newnode;
}

be careful!!! Here, a first address is defined to store d1. If it is not defined in advance, phead - > next = newnode; If head no longer stores d1 address, you can't find d1. Of course, if you just don't want to define a first to store the d1 address first. How? "Connect first and then disconnect". The newnode driver connects to the d1 node first, and then the head node driver connects to the newnode.

3. Header deletion

Head deletion is also similar to the previous two ideas

Header deletion is to delete the d1 node. We define two pointers to d1 and d2 respectively, then connect the back driver of the head node to d2, and the front driver of d2 to head, as shown in the following figure:

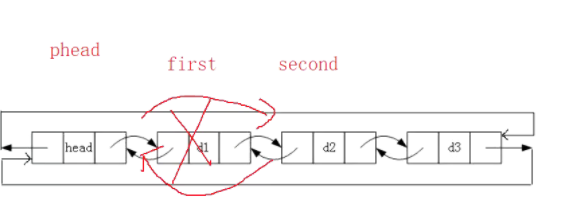
The code is as follows (example):

void ListPopFront(ListNode*phead)
{
	assert(phead);
	ListNode*first = phead->next;
	ListNode*second = first->next;
	phead->next = second;
	second->prev = phead;
}

4. Deletion

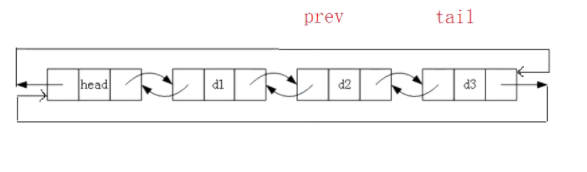
Now to delete the node d3, we define a tail and prev pointer pointing to d3 and d2 respectively, and then connect the d2 rear driver to head and the head front driver to d2, as shown in the following figure:

The code is as follows (example):

void ListPopBack(ListNode*phead)
{
	assert(phead);
	assert(phead->next != phead);//To perform tail deletion, at least one node (non head node) must be deleted
	ListNode*tail = phead->prev;//The head node precursor points to the tail
	ListNode*prev = tail->prev;//Get the d2 address through the tail
	prev->next = phead;//d2 rear drive head node
	phead->prev = prev;//The head precursor points to the d2 node
}

5. Insert data anywhere

To insert data in front of a certain location, you need to find out where that location is. Let's write a lookup function first

How to find it? Very simple, define a cur pointer, and then traverse from d1 to see if there is the data we want to find, and traverse to the end of the head node.
The code is as follows (example):

ListNode* ListFind(ListNode*phead, LTDataType x)
{
	assert(phead);
	ListNode*cur = phead->next;
	while (cur != phead)
	{
		if (cur->data == x)
		{
			return cur;
		}
		cur = cur->next;
	}
	return NULL;//After traversing the linked list, it returns a null pointer if it is not found
}

After finding the required position, the insertion operation is performed

void ListInsert(ListNode*pos, LTDataType x)
{
	assert(pos);
	ListNode*prev = pos->prev;
	ListNode*newnode = BuyListNode(x);
	prev->next = newnode;
	newnode->prev = prev;
	newnode->next = pos;
	pos->prev = newnode;
}

It is also very simple to call the two functions together. For example, I want to insert 300 before the position of data 3 in the linked list. The following two lines of code can complete the application of the two functions.

ListNode*pos = ListFind(plist, 3);
ListInsert(pos, 300);

ps: find the required position pointer here. If necessary, you can also modify the value of the position through this pointer, such as (returned pointer) - > data = n

6. Delete data anywhere

How do I delete the pos data now? It's simple! Define a prev to point to the node before the pos, define a next to point to the node after the pos, and then connect prev and next, as shown in the figure:

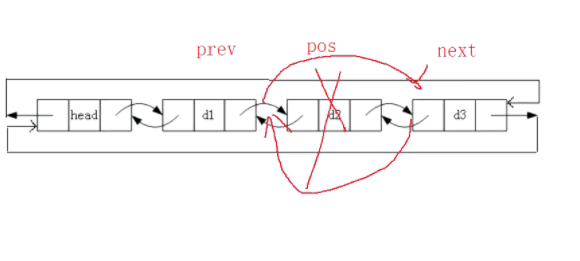
The code is as follows (example):

void ListErase(ListNode*pos)//Delete at specified location
{
	assert(pos);
	ListNode*prev = pos->prev;
	ListNode*next = pos->next;
	prev->next = next;
	next->prev = prev;
	free(pos);//When prev and next are connected, pos can be released
}

4, Print linked list

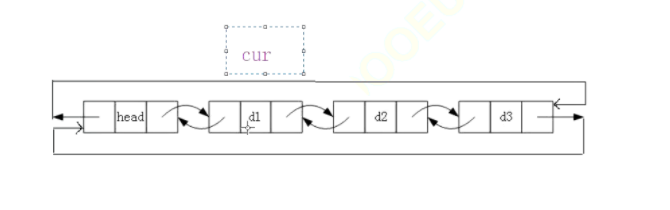
The above figure is an example: to print a linked list, the head node does not need to be printed. We only need to print d1, d2 and d3 that store the actual data. Define a variable cur and let it traverse from d1 to the end of the head node.
The code is as follows (example):

void ListPrint(ListNode*phead)
{
	ListNode*cur = phead->next;
	while (cur != phead)
	{
		printf("%d\n", cur->data);
		cur = cur->next;
	}
	printf("\n");
}

summary

This paper introduces the leading circular bidirectional linked list, including its definition, each interface function, traversal and printing. Although it is the most complex structure in the linked list, its code operation is the simplest. I hope readers can gain something from today's study!