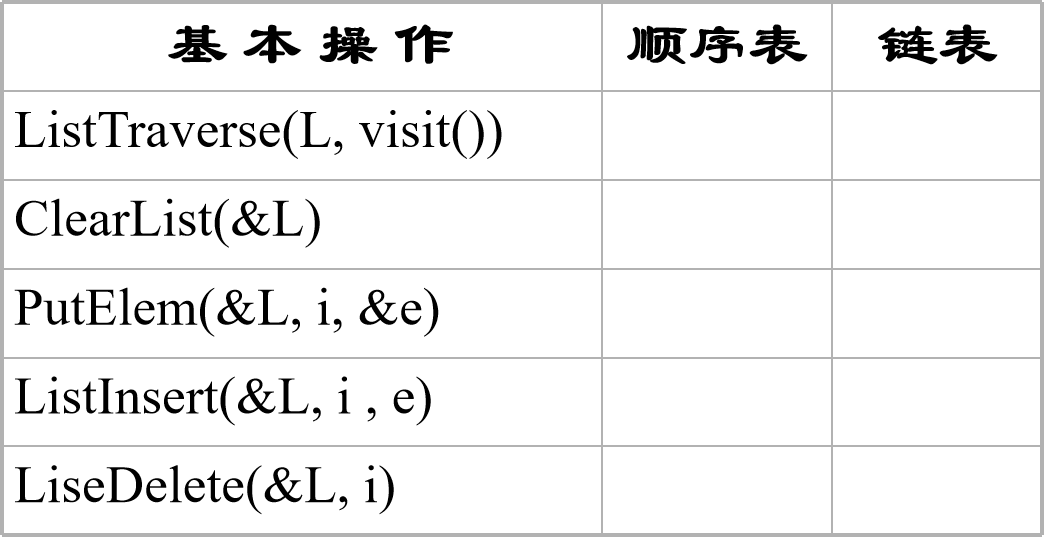
The basic characteristics of linear structure:

I. Basic Concepts of Linear Tables

Linear table L is n(n < 0) data elements a1, a2, a3, with the same attributes. A finite sequence consisting of an, in which the number n of elements in the sequence is called the length of a linear table.

When n=0, it is called an empty table, that is, it contains no elements.

Non-empty linear tables (n > 0) are often recorded as:
(a1，a2，...an)

The data element ai(1 < i < n) is only an abstract symbol, and its concrete meaning can be different under different circumstances.

Logical characteristics of non-empty linear tables:
There is and only one starting node a1, which has no direct forward trend and only one direct successor a2.
There is and only one terminal node, an, which has no direct succession and only one direct forward trend, an-1.
The other nodes ai(2 < i < n-1) have only one direct forward ai-1 and one direct successor ai+1.
Operations are defined on the logical structure, and the concrete implementation of operations is carried out on the storage structure.

Type Definition of Linear Tables

The above problems can be deduced as follows:
By expanding the linear table LA, the data elements existing in the linear table LB but not in the LA are inserted into the linear table LA.



Analysis: Let La=(a1,... ai,... , an)
Lb= (b1，...，bi，...，bm)
Lc= (c1，...，ck，...，cm+n)
Then ck=? k=1, 2,... m+n
The current elements ai and bj are obtained from LA and LB respectively.
If ai<= bj, insert AI into Lc; otherwise insert BJ into Lc.

Void  MergeList(List La，List Lb，List &Lc)
//Data Elements in Linear Table LA and Linear Table LB by Value Non-recursive Emission Reduction Sequence
//A new linear table LC is obtained by merging LA and LB. Elements in LC are still listed by value non-recursive emission reduction.
     InitList(Lc);
     i=j=1;
     k=0;
     La_len=ListLength(La);
     Lb_len=ListLength(Lb);
     while((i<=La_len)&&(j<=Lb_len)){    
     	GetElem(La,i,ai);
     	GetElem(Lb,j,bj);
     	if(ai<=bj){
     		ListInsert(Lc,++k,ai);
            ++i;
        }
      	else{
      		ListInsert(Lc,++k,bj);
            ++j;
        }
      }
      while(i<=La_len){
          GetElem((La,i++,ai);
          ListInsert(Lc,++k,ai);
       }
      while(j<=Lb_len){
          GetElem((Lb,j++,bj);
          ListInsert(Lc,++k,bj);
       }
}

boolisEqual(List LA, List LB) {
 // If the linear table LA and LB are not only equal in length, but also contain data
  // If the element is the same, TRUE is returned, otherwise FALSE is returned.
  	La_len = Listlength(LA);
  	Lb_len = Listlength(LB);
  	if ( La_len != Lb_len )
  		return FALSE; // The lengths of the two tables are unequal
	else 
	{
		i = 1;  found = TRUE;
		while (i<= La_len && found ) {
			GetElem(LA, i, e);  
			if (LocateElem(LB, e, equal( ))
			    i++;  
			else  found = FALSE; 
		}
		return found; 
	}
}

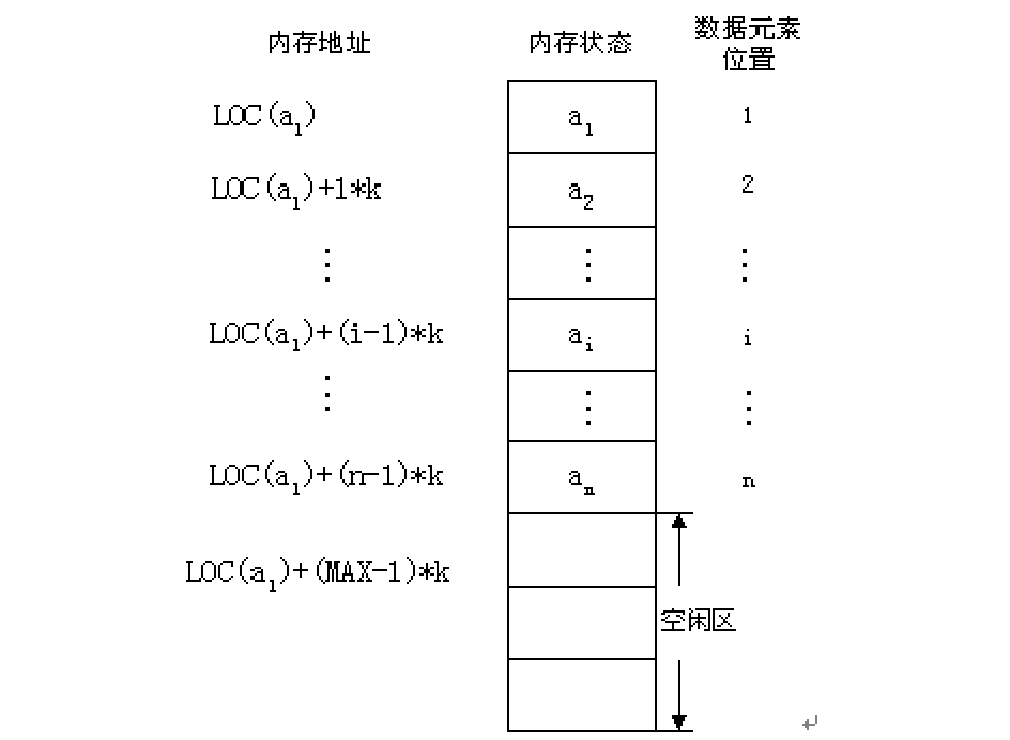
3. Realization of Linear Table Type: Sequential Mapping

—— The logical relationship < x, y > is expressed by a certain relationship between the storage location of X and that of y.
The simplest sequential mapping method is:
Make the storage location of y adjacent to that of x.


In C language, the following type definitions can be used to describe the sequence table:

     #define LIST_INIT_SIZE  100
     #define LISTINCREMENT  10 
     typedef  struct {
               ElemType *elem; 
               int      length;   
               int      listsize；
      }sqList;
      sqList   L;               

In practical applications, ElemType needs to be defined as an actual type

1. Initialization of Linear Tables

Initialization of Sequence Table: Assign a predefined size array space to the Sequence Table and set the current length of the Linear Table to 0.

Status InitList_Sq(SqList &L){  
	L.elem=(ElemType*)malloc(LIST_INIT_SIZE*sizeof(ElemType));
	if(!L.elem)
		exit(OVERFLOW);
	L.length=0;
	L.listsize= LIST_INIT_SIZE;
	return ok;
} 

2. The implementation of LocateElem, a search algorithm for sequential tables:

int LocateElem_Sq(SqList L, ElemType e,status(*compare)( ElemType, ElemType)){ 
     i=1;
     p=L.elem;
     while(i<=L.length && !(*compare )(*p++，e))
		++i；
    if(i<=L.length)  
		return  i ;
    else  
   		return  0;
}   

3. Implementation of ListInsert (&L, i, e) algorithm for inserting sequential tables

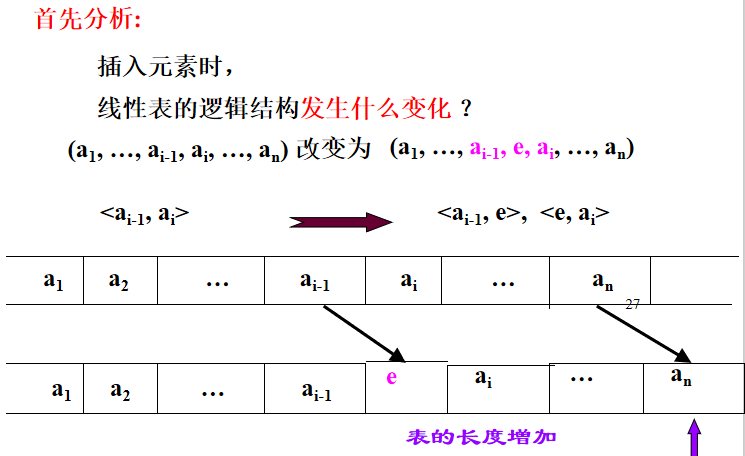
Status compare(int x, int y){
	if (x == y){
		return OK;
	}
	else
	{
		return ERROR;
	}
}
//2. Insertion of Sequence Table
Status ListInsert_Sq(SqList &L, int i, ElemType e){
	ElemType *newbase, *q, *p;
	if (i<1 || i>L.length + 1){
		return ERROR;
	}
	if (L.length >= L.listsize){
		newbase = (ElemType *)realloc(L.elem, (L.listsize + LISTINCREMENT)*sizeof(ElemType));
		if (!newbase)
		{
			exit(OVERFLOW);
		}
		L.elem = newbase;
		L.listsize += LISTINCREMENT;
	}
	q = &(L.elem[i - 1]);
	for (p = &(L.elem[L.length-1]); p >= q; --p)
	{
		*(p + 1) = *p;
	}
	*q = e;
	++L.length;
	return OK;
}

Consider the average of moving elements:

Assuming that the probability of insertion before the first element is pi, the expected number of moving elements required to insert an element into a linear table of length n is: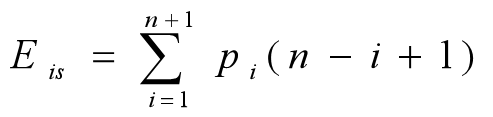

Assuming that the probability of insertion is equal at any position in the linear table, the expected value of the moving element is:

4. Implementation of ListDelete (& L, i, & e) for deleting order table

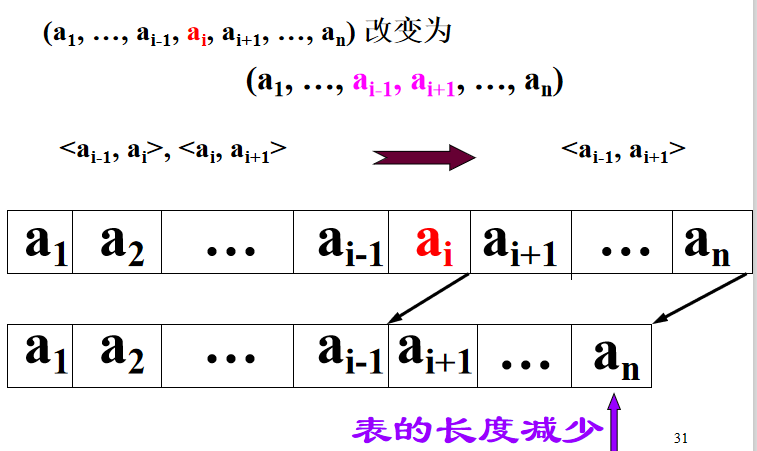
Linear table deletion algorithm:

//4. Deletion of Sequence Table
Status ListDelete_Sq(SqList &L, int i, ElemType &e){
	if ((i<1)||(i>L.length))
	{
		return ERROR;
	}
	ElemType *p, *q;
	p = &(L.elem[i - 1]);
	e = *p;
	q = L.elem + L.length - 1;
	for (p++; p <= q; p++){
		*(p - 1) = *p;
	}
	L.length++;
	return OK;
}

The storage address of any data element in the sequential storage structure of linear table can be derived directly from the formula, so the linear table of sequential storage structure can access any element randomly. However, the sequential storage structure also has some inconveniences, mainly in:

(1) The maximum number of data elements needs to be pre-determined, so that the compiler system of high-level programming language needs to pre-allocate the corresponding storage space;

(2) The efficiency of insertion and deletion operations is very low. In order to maintain the order of data elements in linear tables, large amounts of data need to be moved during insertion and deletion operations. For linear insertion and deletion operations, it will be difficult to improve the speed of the system.

4. Realization of Linear Table Type-Chain Mapping

1. Single linked list

A set of storage units with arbitrary addresses is used to store data elements in linear tables.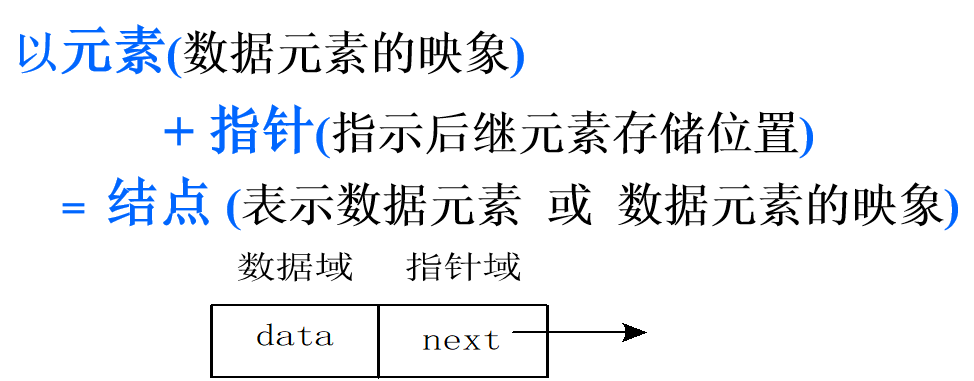

Linear lists are represented by "sequence of nodes" - called single linked lists

C Language Description of Single Linked List

typedef struct  LNode {
      ElemType      data;  // Data Domain
      struct LNode   *next;  // Pointer field
} *LinkList;  
LinkList  L；  // L is the header pointer of a single linked list

Single linked list can be divided into two types: leading node and non-leading node.
For an empty list, the pointer field of the header node is empty. The following is a chain representation of the leading nodes: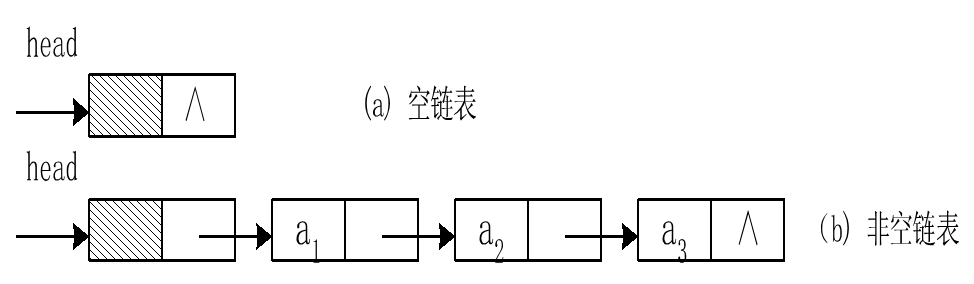

Suppose there is a linear table (A,B,C,D,E) with 10 storage nodes in the storage space. The storage of the linear table in the storage space is shown in Figure 2-7(a).

2. Implementation of single linked list operation

The implementation of GetElem (L, i, &e) in single linked list:
Single linked list is a sequential access structure. In order to find the first data element, we must first find the first data element.

Therefore, the basic operation of finding the first data element is as follows:

Move the pointer, compare j and i

Make pointer p always point to the j th data element in the linear table

Basic operation: Make pointer p always point to the j th data element in the linear table

Status LinkInsert_L(LinkList &L, int i, ElemType e){
	LinkList p,s;
	int j = 0;
	p = L;
	while (p&&j<i-1)
	{
		p = p->next;
		++j;
	}
	if (!p || j>i - 1){
		return ERROR;
	}
	s = (LinkList)malloc(sizeof(LNode));
	s->data = e;
	s->next = p->next;
	p->next = s;
	return OK;
}

Time complexity: O (List Length (L))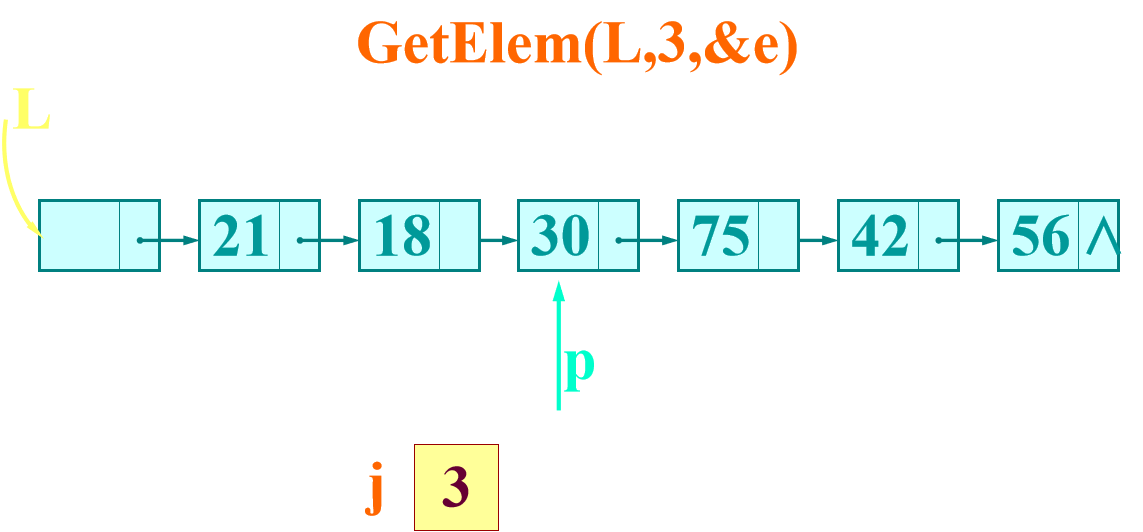

The implementation of ListInsert (&L, i, e) in single linked list: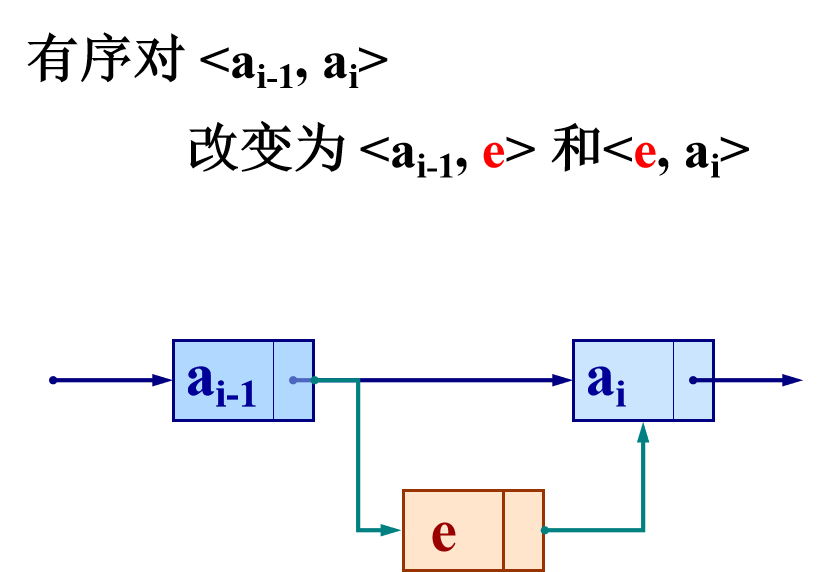


The implementation of ListDelete (&L, i, & e) in linked list:

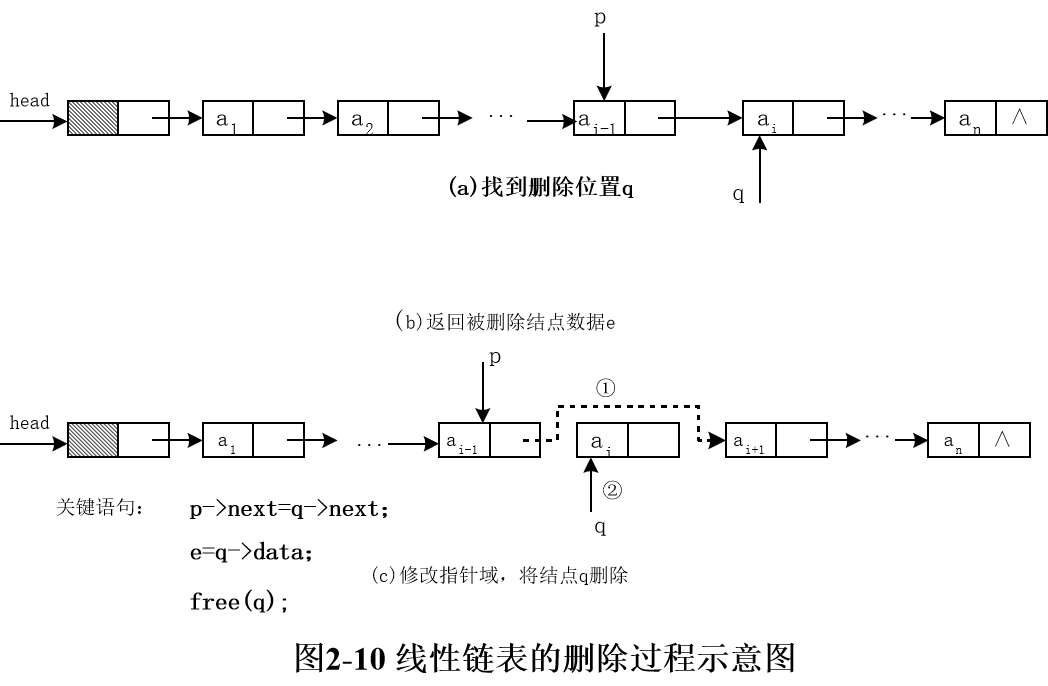
Status ListDelete(LinkList L, int i, ElemType &e){
	LinkList p, q;
	int j;
	p = L;
	j = 0;
	while (p->next&&j<i-1)
	{
		p = p->next;
		++j;
	}
	if (!(p->next) || j>i - 1){
		return ERROR;
	}
	q = p->next;
	p->next = q->next;
	e = q->data;
	free(q);
	return OK;
}

Time complexity of the algorithm: O(ListLength(L))
The implementation of ClearList (&L) in linked list:

void ClearList(LinkList &L){
	LinkList p;
	while (L->next)
	{
		p = L->next;
		L->next = p->next;
		free(p);
	}
}

Algorithmic time complexity: O(ListLength(L))
How to get single linked list from linear list?
Linked list is a dynamic structure, it does not need to pre-allocate space, so the process of creating linked list is a process of "inserting nodes one by one".

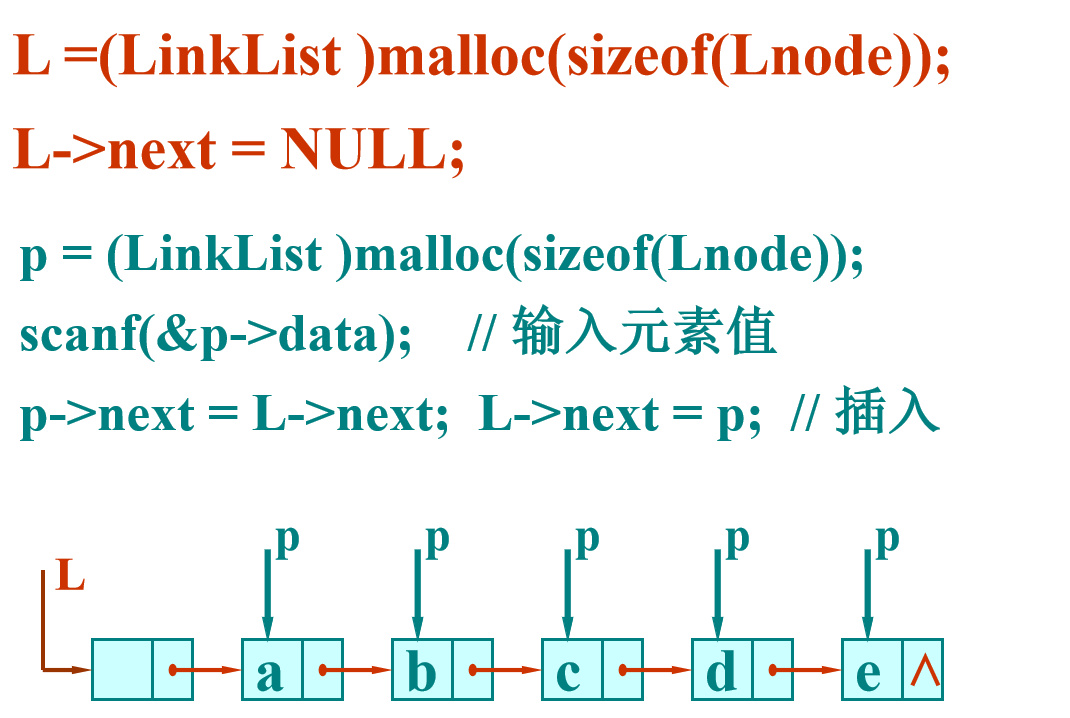
void CreteList(LinkList &L, int n){
	LinkList p;
	L = (LinkList)malloc(sizeof(LNode));
	L->next = NULL;
	for (int i = n; i > 0; --i)
	{
		p = (LinkList)malloc(sizeof(LNode));
		scanf("%d",&p->next);
		p->next = L->next;
		L->next = p;
	}
}

The time complexity of the algorithm is O(Listlength(L))

MergeList_L operation (single linked list)

Status MergeList_L(LinkList &La, LinkList &Lb, LinkList &Lc){
	LNode *pa, *pb, *pc;
	pa = La->next;
	pb = Lb->next;
	Lc = pc = La;
	while (pa&&pb)
	{
		if (pa->data<=pb->data)
		{
			pc->next = pa;
			pc = pa;
			pa = pa->next;
		}
		else
		{
			pc->next = pb;
			pc = pb;
			pb = pb->next;
		}
	}
	pc->next = pa ? pa : pb;
	free(Lb);
}

When using the single linked list defined above to realize the operation of linear list, there are some problems:

The list length of a single linked list is an implicit value.
When inserting elements at the last position of the single list, the whole list needs to be traversed.
In the list, the concept of "order" of elements is weakened, and the concept of "location" of nodes is strengthened.

Improve the list settings:

Increase "table length", "table tail pointer" and "current position pointer" three fields;
Change the basic operation from "order" to "pointer".

Single linked list with tailed pointer

MergeList_L operation (single linked list with tail pointer)
The ordered list LA and the ordered list LB are merged into LC in an orderly manner.

Status MergeList_L(LinkList &La, LinkList &Lb, LinkList &Lc, 
                            int (* compare)(ElemType, ElemType)){
     if(!InitList(Lc)) return ERROR;
     ha = GetHead(La); hb = GetHead(Lb);
     pa=NextPos(La,ha); pb=NextPos(Lb,hb); 
     while(pa &&pb){
          a = GetCurElem(pa); b = GetCurElem(pb); 
   if((* compare)(a,b)<=0){
          DelFirst(ha,q);  Append(Lc,q);  pa=NextPos(La,ha);}
    else{
   DelFirst(hb,q);  Append(Lc,q);  pb=NextPos(Lb,hb);}
}
if(pa) Append(Lc,pa);
else   Append(Lc,pb);
       FreeNode(ha); FreeNode(hb); 
       return ok;		
}

4. Static linked list

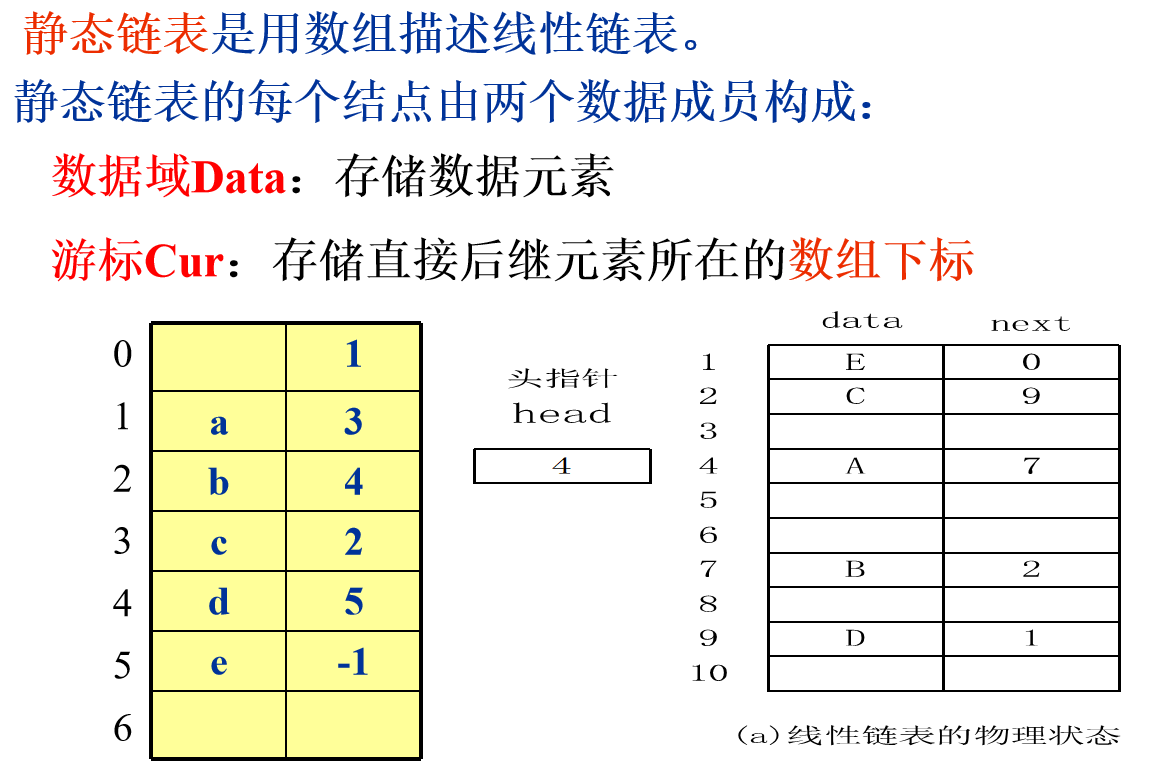
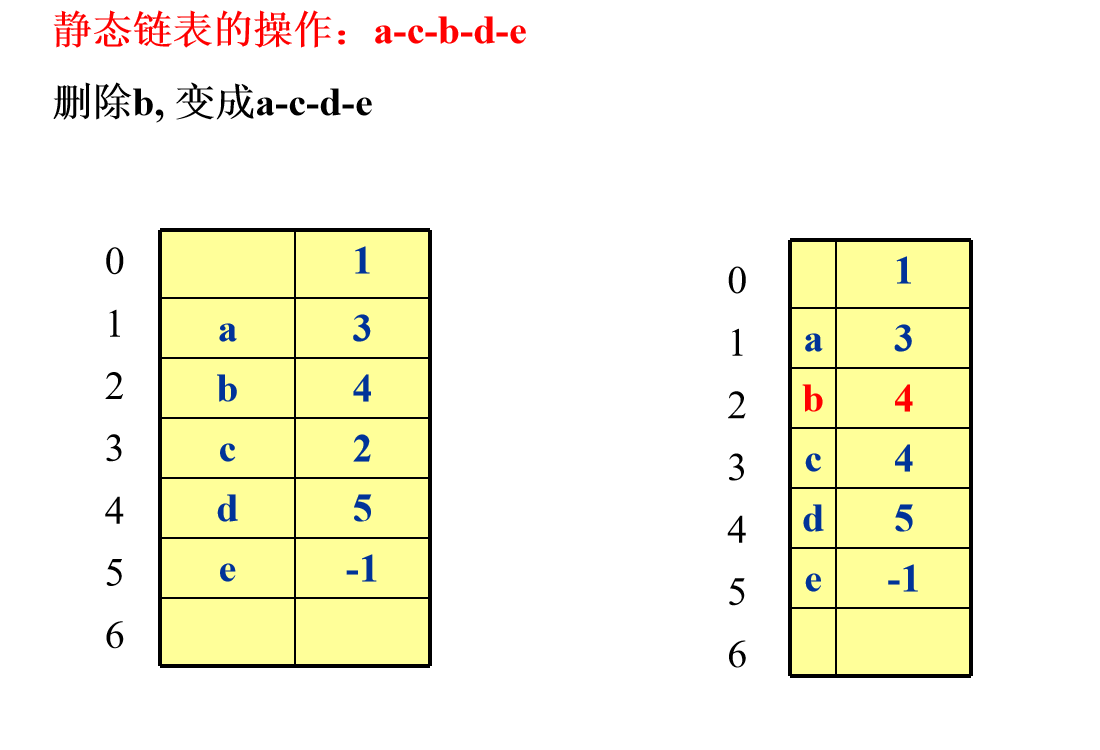
Storage structure design of static linked list

#define MAXSIZE 1000
typedef struct{
	ElemType data;
	int cur;	
}component, SLinkList[MAXSIZE];

Operation Design of Static Link List

int LocateElem_SL(SLinkList S, ElemType e){
	i = S[0].cur;
	while(i!=-1 && S[i].data != e)
		i = S[i].cur;
	return i;
} //LocateElem_SL

5. Circular linked list

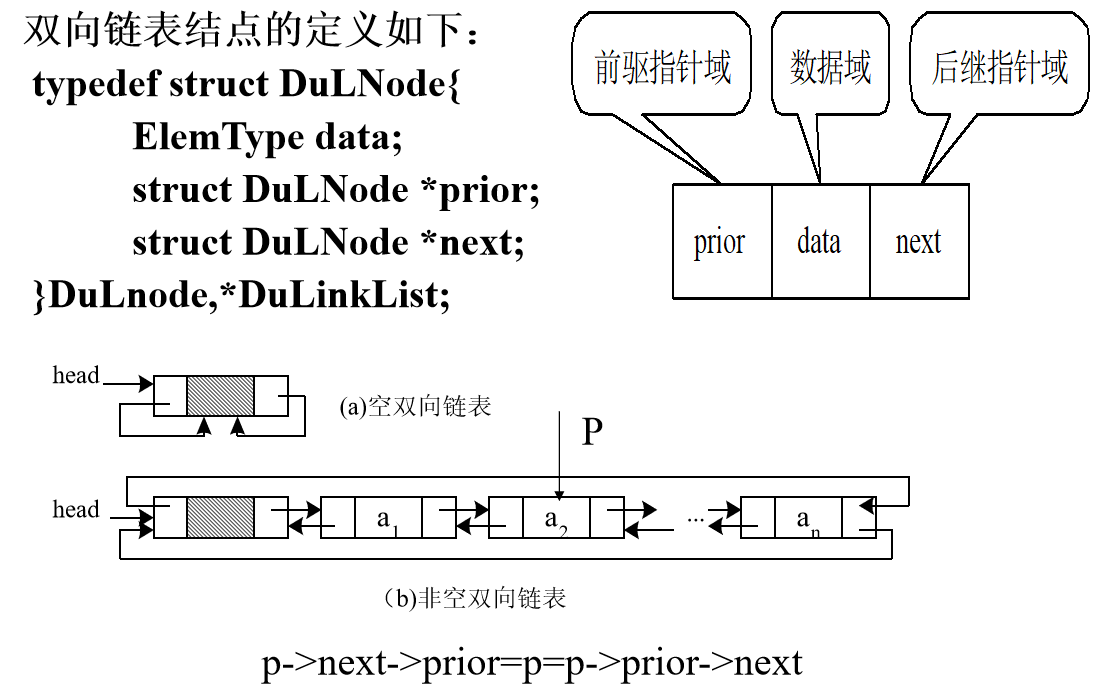
6. Bidirectional linked list

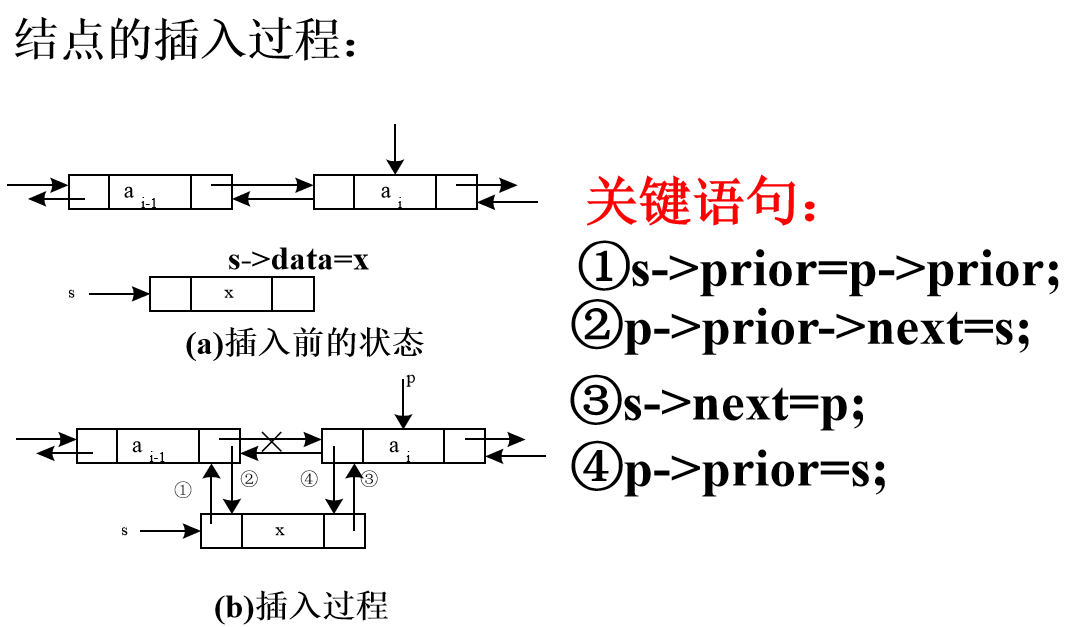
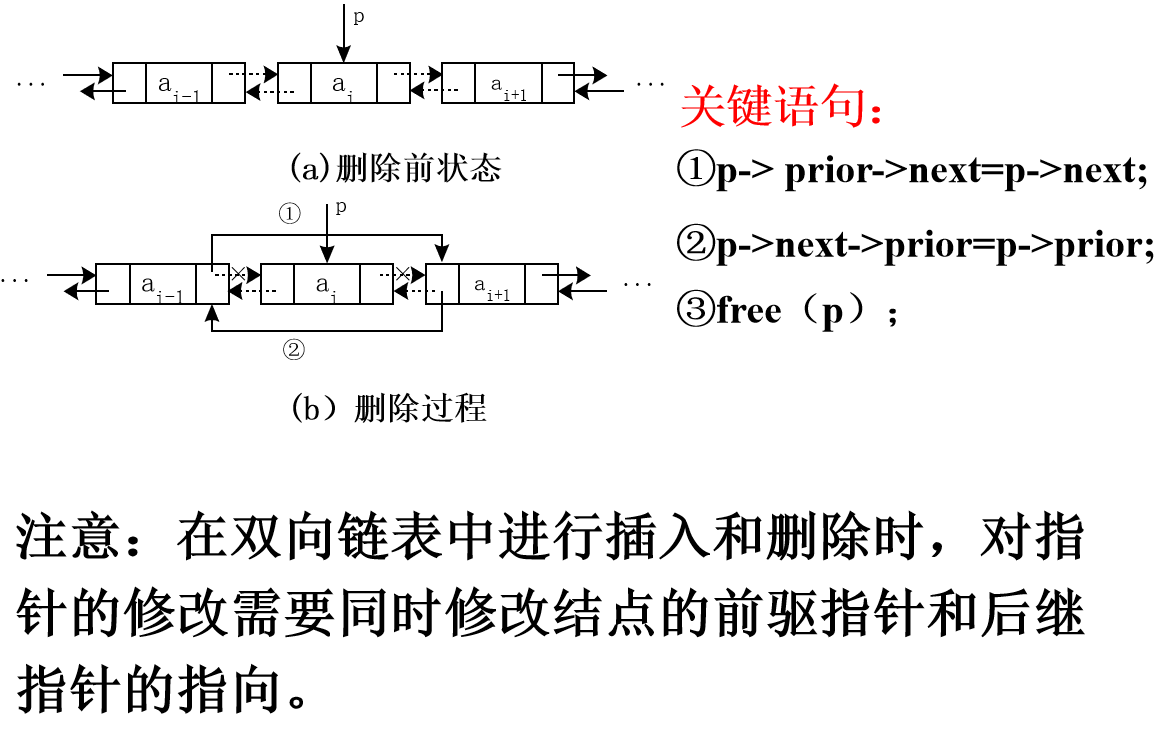
5. Application of Linear Tables: Representation and Addition of Univariate Polynomials

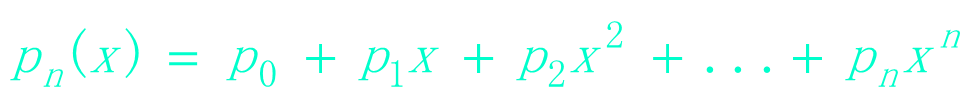
In a computer, it can be represented by a linear table:
P = (p0, p1, ...，pn)
But for example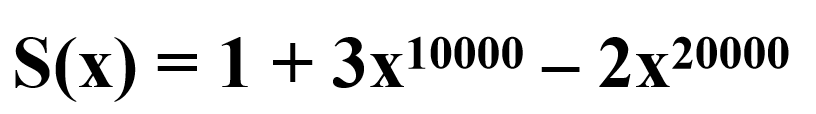

Is the above representation appropriate for polynomials?

1. Definition of unary polynomial of abstract data type:

2. The sum of univariate polynomials

Suppose that polynomials are represented by a single linked list: A(x)=12+7x+8x10+5x17, B(x)=8x+15x7-6x10, and head pointers ha and hb point to the two linked lists respectively, as shown in Figure 2-21: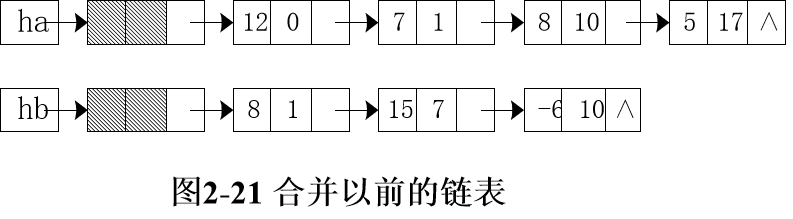

By adding two polynomials, the result is C(x)= 12+15x+15 x7+2x10+5x17. As shown in Figure 2-22.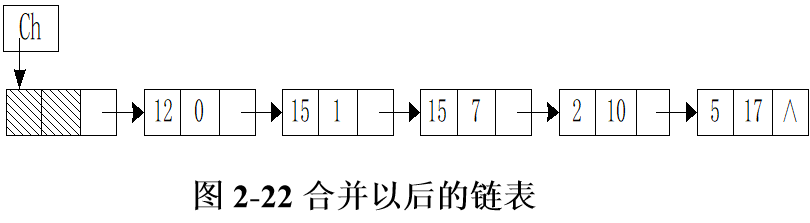

Rules for the addition of two unary polynomials: suppose that the pointers qa and qb point to a node in the polynomial A(x) and B(x), respectively, which is currently being compared, the exponential terms of the two node data domains need to be compared. There are three cases:

(1) when the exponential value of the node indicated by qa is less than the exponential value of the node indicated by qb, the node indicated by qa is retained and qa moves backward.

(2) when the exponential value of the node indicated by QA > the exponential value of the node indicated by qb, the node indicated by QB is inserted before the node indicated by qa, and the QB moves backward.

(3) When the exponential value of the node indicated by qa equals the exponential value of the node indicated by qb, the coefficients of the two nodes are added together. If it is not zero, the coefficients of the nodes referred to in qa are modified, and the nodes referred to in QB are released at the same time. On the contrary, the corresponding nodes are deleted from the list of polynomial A(x), and the nodes referred to in qa and QB are released.
Polynomial addition algorithm:

Void  addpolyn(polynomial &pa, polynomial &pb)
{
     ha=GetHead(pa);
     hb=GetHead(pb); 
          //ha and hb point to the head nodes of two linked lists, respectively
     qa=NextPos(pa,ha); 
     qb=NextPos(pb,hb);
           //qa and qb point to the current nodes in pa and pb, respectively
       while(qa&&qb) { //Neither list is empty 
   a=GetCurElem(qa);b=GetCurElem(qb);//
   Switch(*cmp(a,b)){
      case –1:
          ha=qa;qa= NextPos(pa,qa);break;
      case 0: //The exponential values of the two are equal.
          sum=a.coef+b.coef;
          if(sum!=0.0){//When the additive coefficient is not zero
              SetCurElem(qa,sum);ha=qa;}
          else{//When the additive coefficient is zero
                DelFirst(ha,qa);FreeNode(qa);}    
         DelFirst(hb,qb);FreeNode(qb);qb=NextPos(pb,hb);
         qa=NextPos(pa,ha); break;      
               case 1:polynomial pb Small exponential value
              DelFirst(hb,qb);InsFirst(ha,qb);
              qb=NextPos(pb,hb);  ha=NextPos(pa,ha);break;
       }//switch
     }//while
    if (!ListEmpty(pb)  Append(pa,qb);
    FreeNode(hb);
} //Addpolyn

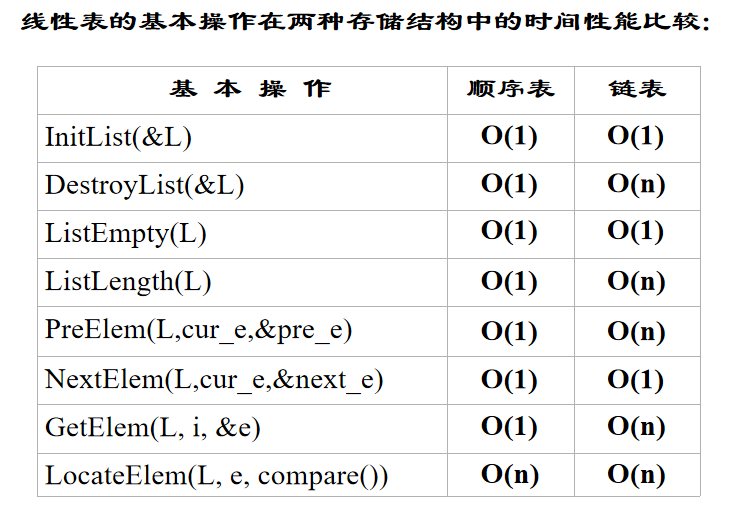
Comparison of Sequence List and Chain List

Sequence list and linked list have their own shortcomings and shortcomings, so they should be selected according to the requirements and nature of the problem in practical application. Sequential storage has three advantages:
(1) The method is simple and easy to implement.
(2) No additional storage overhead is needed to represent the logical relationship between nodes.
(3) It has the characteristics of random access according to element number.
Two major drawbacks:
(1) When insertion/deletion operations are performed in the sequential table, about half of the elements in the table are moved on average, so the operation efficiency of the sequential table is low when n is large.
(2) Sufficient storage space needs to be allocated in advance. If the estimation is too large, it will easily lead to a large number of idle at the back of the sequence table; if the pre-allocation is too small, it will cause overflow.
The advantages and disadvantages of linked lists are just the opposite of sequential lists. How to choose the appropriate storage structure in practice? Usually the following points can be considered:
1. Space-based considerations
The storage space of sequential tables is statically allocated, and its storage size must be specified clearly before the program is executed. If the length of linear table n varies greatly, it is difficult to accurately estimate the storage size in advance. It is estimated that too large will cause space waste, and too small will increase the chance of space spillover. Therefore, when it is difficult to estimate the length or storage size of linear tables, sequential storage structure should not be used.
The linked list does not need to estimate the storage size beforehand. It is a dynamic allocation. As long as memory space is free, no overflow will occur. Therefore, when the length of linear table changes greatly and it is difficult to estimate its storage size, it is better to use dynamic linked list as storage structure. But the storage density of linked list is low. Storage density refers to the ratio of the storage unit occupied by data elements in a node to the storage unit occupied by the whole node. Obviously, the storage density of chain storage structure is less than 1, while that of sequential table is 1.

2. Time-based considerations
Random access structure is that any node in the table can be directly acquired in O(1) time. If the linear table is mainly searched, and insertion and deletion operations are seldom done, the sequential storage structure is preferable, while the time performance of sequential number access in the linked list is O(n). Therefore, if the frequent operation is to access data elements by serial number, the sequential list is obviously better than the linked list.
When inserting and deleting in the sequence table, the average number of elements in the table should be moved; especially when the amount of information of each node is large, the time cost of moving nodes is considerable. To insert and delete at any position in the list, you only need to modify the pointer. For linear tables that are frequently inserted and deleted, it is advisable to use linked list as storage structure. If the insertion and deletion of tables mainly occur at the beginning and the end of the table, it is advisable to use the single-loop linked list represented by the tail pointer.

3. Environmental considerations
Sequential lists are easy to implement, and there are array types in any high-level language. The operation of linked lists is based on pointers, and their use is limited by the language environment, which is also one of the factors that users should consider.
In short, the two storage structures have their own characteristics. The choice of structure depends on the main factors of actual use. Generally, the "stable" linear table chooses sequential storage structure, while the "dynamic" linear table with frequent insertion/deletion should choose chain storage structure.