This paper briefly introduces the concept of tree. The more important are the implementation of heap, heap sorting, TOP-K problem, traversal of binary tree (pre, middle, post order and sequence traversal) and the implementation of binary tree function
catalogue
1, Concept and structure of tree
2, Concept and structure of binary tree
2.2 storage structure of binary tree
3, Sequential structure and implementation of binary tree
3.2 heap sorting (Application of heap)
4, Chain structure of binary tree
4.2 function realization of binary tree
1, Concept and structure of tree
1.1 concept of tree
Tree is a nonlinear data structure. It is a set with hierarchical relationship composed of n (n > = 0) finite nodes. It is called a tree because it looks like an upside down tree, that is, it has roots up and leaves down.
- There is a special node, called the root node, which has no precursor node
- Except for the root node, the other nodes are divided into m (M > 0) disjoint sets T1, T2,..., Tm, and each set Ti (1 < = I < = m) is a subtree with a structure similar to the tree.
- The root node of each subtree has and only has one precursor, and can have 0 or more successors. Therefore, the tree is defined recursively.
Example of tree:
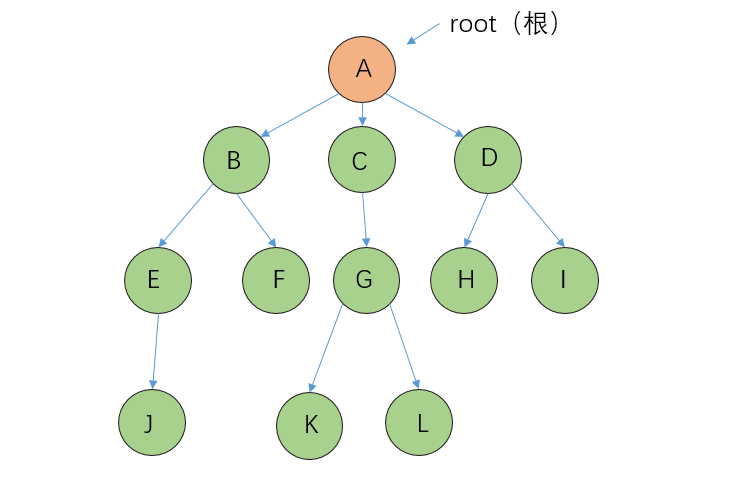
Note: in the tree structure, there must be no intersection between subtrees, otherwise it is not a tree structure
1.2 representation of tree
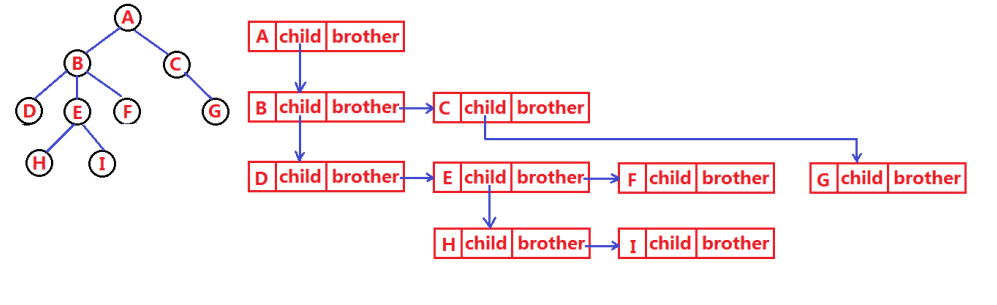
The tree structure is more complex than the linear table, and it is more troublesome to store and express. Since the value range is saved, the relationship between nodes should also be saved. In fact, there are many kinds of tree representations, such as parent representation, child representation, child parent representation, left child right brother representation, etc. Here we learn about the most commonly used expression of left child and right brother. The specific structure is as follows:
typedef int DataType;
struct Node
{
struct Node* child; // first child node
struct Node* brother; // Point to its next sibling node
DataType data; // Data fields in nodes
};
The application of tree in practice includes: the directory tree structure representing the file system, and so on
2, Concept and structure of binary tree
2.1 binary tree concept:
A binary tree is a finite set of nodes, which:
1. Or empty 2. It is composed of a root node and two binary trees called left subtree and right subtree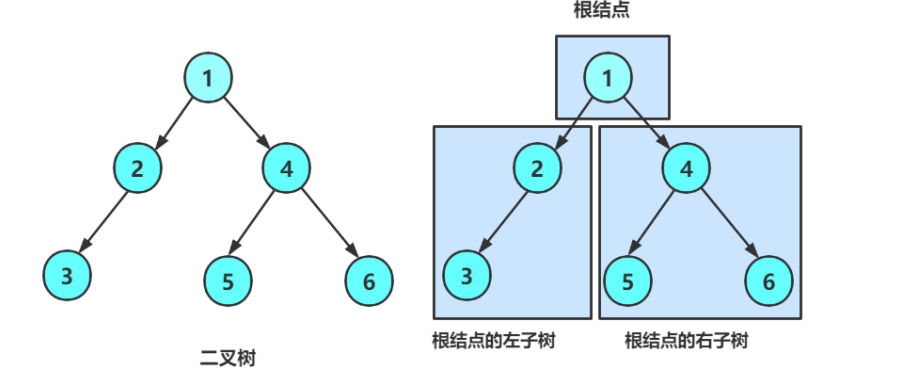
As can be seen from the above figure:
1. The binary tree does not have nodes with a degree greater than 2
2. The subtree of a binary tree can be divided into left and right, and the order cannot be reversed. Therefore, a binary tree is an ordered tree
Note: any binary tree is composed of the following situations:
----------------------
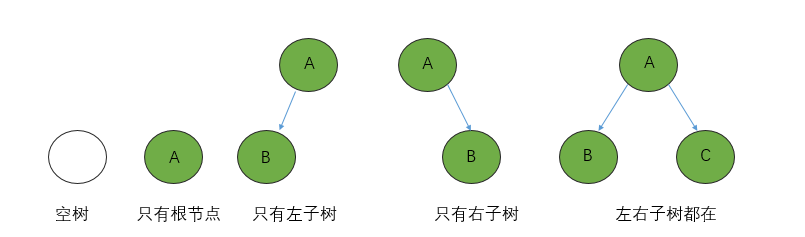
There are two special binary trees:
Full binary tree: a binary tree. If the number of nodes in each layer reaches the maximum, the binary tree is a full binary tree
Complete binary tree: a complete binary tree is a highly efficient data structure. A complete binary tree is derived from a full binary tree
Note: full binary tree is a special complete binary tree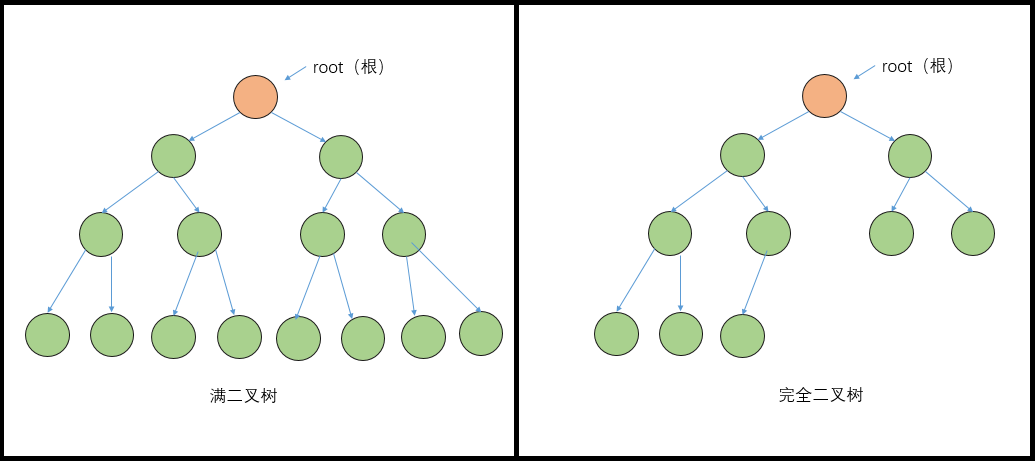
2.2 storage structure of binary tree
Binary tree can be stored in two structures: a sequential structure and a chain structure.
1. Sequential storage
Sequential structure storage is to use arrays for storage. Generally, arrays are only suitable for representing complete binary trees, because there will be a waste of space if they are not complete binary trees. In reality, only the heap will use arrays to store. The sequential storage of binary tree is an array physically and a binary tree logically.
2. Chain storage
The chain storage structure of binary tree is to represent a binary tree with a linked list, that is, to indicate the logical relationship of elements with a chain. The usual method is that each node in the linked list is composed of three fields, data field and left and right pointer field. The left and right pointers are used to give the storage address of the chain node where the left child and right child of the node are located respectively.
3, Sequential structure and implementation of binary tree
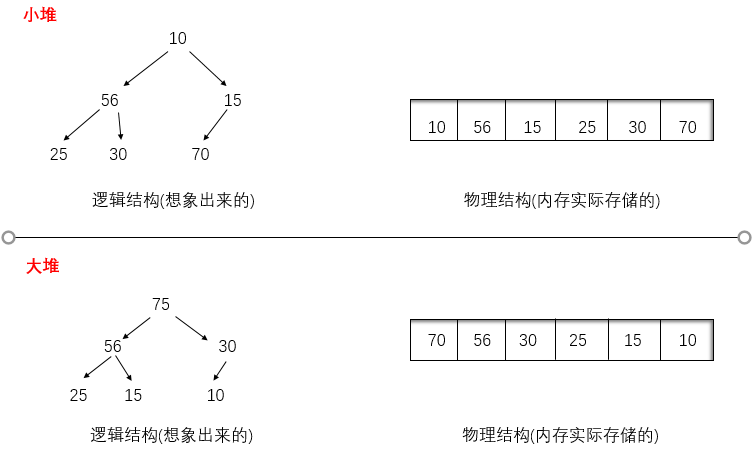
Ordinary binary trees are not suitable for storing with arrays, because there may be a lot of space waste. The complete binary tree is more suitable for sequential structure storage. In reality, we usually store the heap (a binary tree) in an array of sequential structures. The heap with the largest root node is called the maximum heap or large root heap, and the heap with the smallest root node is called the minimum heap or small root heap.
Nature of heap: 1. The value of a node in the heap is always not greater than or less than the value of its parent node
2. Heap is always a complete binary tree
3.1 realization of heap:
The following are the implementation of small heap
matters needing attention:
1. After inserting the heap, it must be ensured that the heap is still a small heap, so after inserting the data, it must be adjusted upward to ensure that the heap is still a small heap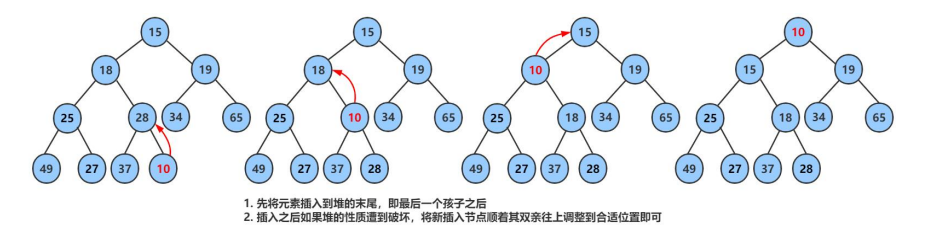
tip: it is known that the child subscript is child(10 in the above figure is the child node), whether it is a left child or a right child, parent=(child-1)/2
2. Heap deletion is to delete the data at the top of the heap, change the last data of the data root at the top of the heap, then delete the last data of the array, and then carry out the downward adjustment algorithm (the downward adjustment algorithm has a premise: the left and right subtrees must be a heap before adjustment), and keep the heap or a small heap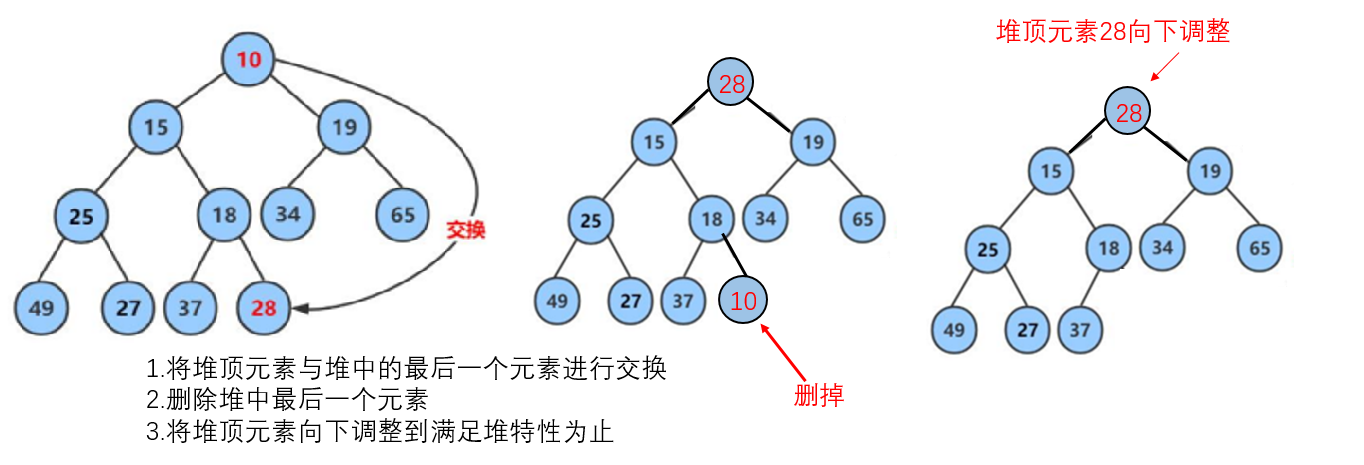
tip: parent is the subscript of the parent node (Figure 28 above shows the parent node)
Left child subscript: leftchild=parent*2+1, right child subscript: rightchild=parent*2+2
heap.h header file:
#pragma once
#include<stdio.h>
#include<stdlib.h>
#include<stdbool.h>
#include<assert.h>
#include<time.h>
typedef int HPDataType;
typedef struct Heap
{
HPDataType* a;
int size;
int capacity;
}Heap;
// Heap construction
void HeapInit(Heap* hp);
// Heap destruction
void HeapDestroy(Heap* hp);
// Heap insertion
void HeapPush(Heap* hp, HPDataType x);
// Deletion of heap
void HeapPop(Heap* hp);
// Take the data from the top of the heap
HPDataType HeapTop(Heap* hp);
// Number of data in the heap
int HeapSize(Heap* hp);
// Empty judgment of heap
bool HeapEmpty(Heap* hp);
//Upward adjustment
void Adjustup(HPDataType*a, int child);
//Downward adjustment
void Adjustdown(HPDataType*a, int size, int parent);
//Print heap
void HeapPrint(Heap*hp);Code implementation (heap.c):
#include"heap.h"
void swap(HPDataType*a, HPDataType*b)
{
HPDataType tmp = *a;
*a = *b;
*b = tmp;
}
void Adjustup(HPDataType*a, int child)
{
assert(a);
int parent = (child - 1) / 2;
while (child > 0)
{
//For a lot of words, replace '<' in a [child] < a [parent] with '>'
if (a[child] < a[parent])
{
swap(&a[child], &a[parent]);
child = parent;
parent = (child - 1) / 2;
}
else
break;
}
}
void HeapPrint(Heap*hp)
{
for (int i = 0; i < hp->size; i++)
{
printf("%d ", hp->a[i]);
}
printf("\n");
}
void Adjustdown(HPDataType*a, int size, int parent)
{
//Adjust it down, turn it into a small pile and exchange it with the youngest of the left and right children
//End condition: the value of the parent node < = the value of the young child or directly adjusted to the leaf
assert(a);
int child = parent * 2 + 1;
while (child<size)
{
//If the right child is smaller than the left child, let the child subscript + +, making it a right child
//child+1 ensures that the child's subscript is within the valid range
if (child + 1 < size&&a[child + 1] <a[child])//Replace '<' with '>' in a [child + 1] < a [child]
{
child++;
}
if (a[child]<a[parent])//For a lot of words, replace '<' in a [child] < a [parent] with '>'
{
swap(&a[child ], &a[parent]);
parent = child;
child = parent * 2 + 1;
}
else
break;
}
}
// Heap construction
void HeapInit(Heap* hp)
{
assert(hp);
hp->a = NULL;
hp->size = hp->capacity = 0;
}
// Heap destruction
void HeapDestroy(Heap* hp)
{
assert(hp);
free(hp->a);
hp->a = NULL;
hp->size = hp->capacity = 0;
}
// Heap insertion (small heap)
void HeapPush(Heap* hp, HPDataType x)
{
assert(hp);
if (hp->size == hp->capacity)
{
//Judge whether to initialize (capacity is 0 during initialization) or whether the space is full and needs to be increased
int newcapacity = hp->capacity == 0 ? 4 : hp->capacity * 2;
HPDataType*tmp = realloc(hp->a, sizeof(HPDataType)*newcapacity);
if (tmp == NULL)
exit(-1);
hp->a = tmp;
hp->capacity = newcapacity;
}
hp->a[hp->size] = x;
hp->size++;
//After inserting the data, adjust it upward, and adjust the tail, so the subscript is size-1
Adjustup(hp->a, hp->size - 1);
}
// Delete at top of heap
void HeapPop(Heap* hp)
{
assert(hp);
assert(hp->size > 0);
swap(&hp->a[0], &hp->a[hp->size - 1]);//Top and tail exchange
hp->size--;
//Adjust it down to the top of the heap, so the subscript of the father is 0
Adjustdown(hp->a, hp->size, 0);
}
// Take the data from the top of the heap
HPDataType HeapTop(Heap* hp)
{
assert(hp);
return hp->a[0];
}
// Number of data in the heap
int HeapSize(Heap* hp)
{
return hp->size;
}
// Empty judgment of heap
bool HeapEmpty(Heap* hp)
{
return hp->size == 0;
}Code test:
#include"heap.h"
int main()
{
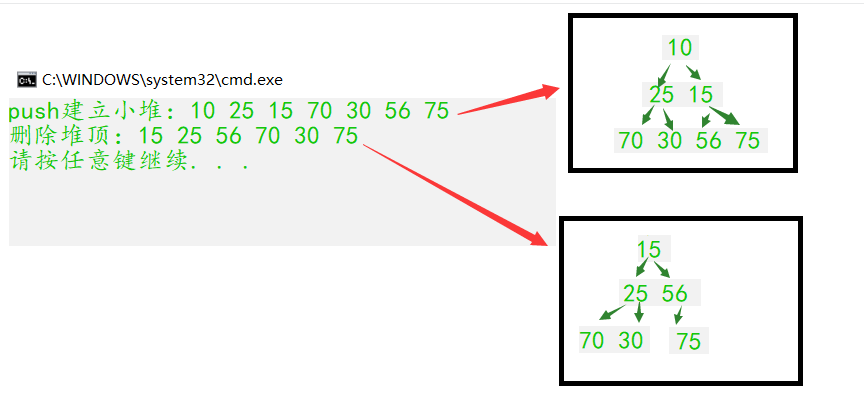
int a[] = { 70, 56, 30, 25, 15, 10, 75 };
Heap hp;
HeapInit(&hp);
for (int i = 0; i < sizeof(a) / sizeof(a[0]);i++)
{
HeapPush(&hp, a[i]);
}
printf("push Build a small heap:");
HeapPrint(&hp);
printf("Delete heap top:");
HeapPop(&hp);
HeapPrint(&hp);
return 0;
} 
3.2 heap sorting (Application of heap)
Heap sorting uses the idea of heap to sort. It is divided into two steps:
1. Pile building
Ascending order: build a pile
Descending order: build small piles
2. Use the idea of heap deletion to sort
Downward adjustment is used in both heap creation and heap deletion, so once you master downward adjustment, you can complete heap sorting.
code:
#include"heap.h"
void HeapSort(int*a, int n)
{ //Build a lot in ascending order. Remember to change the up adjustment and down adjustment symbols
//Because the downward adjustment is used, it must be determined that the left and right subtrees of the root are a lot. Take n-1 as the child node subscript, find the parent node, and traverse from the back of the heap
for (int i = (n - 1 - 1) / 2; i >= 0; i--)
{
Adjustdown(a, n, i);
}
//for (int i = n - 1; i >0; i--)
//{
// Adjustup(a, i);
//}
The top of the heap is exchanged with the tail, and the maximum number is at the tail
for (int i = 0; i < n; i++)
{
swap(&a[0], &a[n - 1 - i]);
//After the exchange, because it is a large number, adjust downward to find a large number, and the number exchanged at the tail is not included in the adjusted length
Adjustdown(a, n - 1 - i, 0);
}
//for (int end = n - 1; end > 0; --end)
//{
// swap(&a[end], &a[0]);
// Adjustdown(a, end, 0);
//}
}
int main()
{
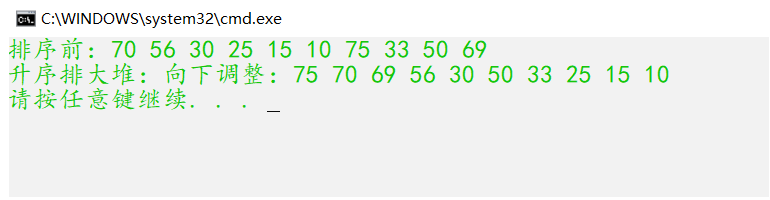
int a[] = { 70, 56, 30, 25, 15, 10, 75 ,33, 50, 69};
printf("Before sorting:");
for (int i = 0; i < sizeof(a) / sizeof(a[0]); i++)
printf("%d ", a[i]);
printf("\n");
printf("In ascending order:");
HeapSort(&a,sizeof(a)/sizeof(a[0]));
printf("Downward adjustment:");
for (int i = 0; i < sizeof(a) / sizeof(a[0]); i++)
printf("%d ", a[i]);
printf("\n");
return 0;
}
3.3TOP-K problem
TOP-K problem: that is to find the first K largest or smallest elements in data combination. Generally, the amount of data is relatively large.
For example, the top 10 professional players, the world's top 500, the rich list, the top 100 active players in the game, etc.
For the Top-K problem, the simplest and direct way you can think of is sorting. However, if the amount of data is very large, sorting is not desirable (maybe all the data can not be loaded into memory at once). The best way is to use heap. The basic idea is as follows:
1. Use the first K elements in the data set to build the heap
For the first k largest elements, build a small heap
For the first k smallest elements, build a lot
2. Compare the remaining N-K elements with the top elements in turn. If not, replace the top elements. After comparing the remaining N-K elements with the top elements in turn, the remaining K elements in the heap are the first K minimum or maximum elements.
code:
#include"heap.h"
void PrintTopK(int* a, int n, int k)
{
//Use a small heap to find the largest element and a large heap to find the smallest element
// 1. Build a small heap -- build a heap with the first k elements in a
Heap hp;
HeapInit(&hp);
int i = 0;
for (i = 0; i < k; i++)
{
//Small pile, change the downward adjustment and upward adjustment to the less than sign
HeapPush(&hp, a[i]);
}
// 2. Compare the remaining n-k elements with the heap top elements in turn, and replace the heap top elements if they are larger than the heap top
for (int j = k; j < n; j++)
{
if (a[j]>HeapTop(&hp))
{
hp.a[0] = a[j];
Adjustdown(hp.a, hp.size, 0);
/*HeapPop(&hp);
HeapPush(&hp, a[i]);*/
}
}
HeapPrint(&hp);
HeapDestroy(&hp);
}
void TestTopk()
{
int n = 10000;
int* a = (int*)malloc(sizeof(int)*n);
srand(time(0));
for (size_t i = 0; i < n; ++i)
{
a[i] = rand() % 1000000;
}
a[5] = 1000000 + 1;
a[1231] = 1000000 + 2;
a[531] = 1000000 + 3;
a[5121] = 1000000 + 4;
a[1] = 1000000 + 5;
a[2335] = 1000000 + 6;
a[9999] = 1000000 + 7;
a[76] = 1000000 + 8;
a[423] = 1000000 + 11;
a[3144] = 1000000 + 10;
PrintTopK(a, n, 10);
}
int main()
{
printf("Top ten largest numbers");
TestTopk();
return 0;
}
4, Chain structure of binary tree
4.1 traversal of binary tree
The so-called binary tree traversal is to operate the nodes in the binary tree in turn according to a specific rule, and each node operates only once. The operation of the access node depends on the specific application problem. Traversal is one of the most important operations on binary tree, and it is also the basis of other operations on binary tree.
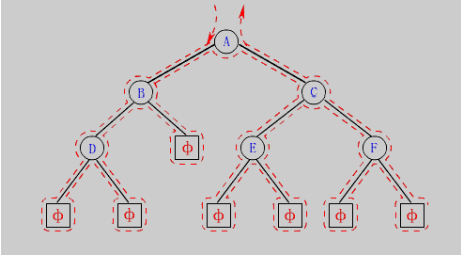
According to the rules, the traversal of binary tree includes: pre order / middle order / post order recursive structure traversal:
1. Preorder Traversal (also known as Preorder Traversal) - the operation of accessing the root node occurs before traversing its left and right subtrees.
2. Inorder traversal - the operation of accessing the root node occurs in traversing its left and right subtrees (between).
3. Postorder traversal - the operation of accessing the root node occurs after traversing its left and right subtrees.
// Preorder traversal of binary tree void PreOrder(BTNode* root); // Order traversal in binary tree void InOrder(BTNode* root); // Postorder traversal of binary tree void PostOrder(BTNode* root);
We create a simple binary tree to traverse the front, middle and back order
typedef char BTDataType;
typedef struct BinaryTreeNode
{
struct BinaryTreeNode*left;
struct BinaryTreeNode*right;
BTDataType data;
}BTNode;
BTNode* BuyNode(BTDataType x)
{
BTNode*node = (BTNode*)malloc(sizeof(BTNode));
if (node == NULL)
exit(-1);
node->data = x;
node->left = node->right = NULL;
return node;
}
BTNode* CreatBinaryTree()
{
BTNode* nodeA = BuyNode('A');
BTNode* nodeB = BuyNode('B');
BTNode* nodeC = BuyNode('C');
BTNode* nodeD = BuyNode('D');
BTNode* nodeE = BuyNode('E');
BTNode* nodeF = BuyNode('F');
nodeA->left = nodeB;
nodeA->right = nodeC;
nodeB->left = nodeD;
nodeC->left = nodeE;
nodeC->right = nodeF;
return nodeA;
}
//Preamble
void PreOrder(BTNode*root)
{
if (root == NULL)
{
printf("NULL ");
return;
}
printf("%c ", root->data);
PreOrder(root->left);
PreOrder(root->right);
}
//Middle order
void InOrder(BTNode*root)
{
if (root == NULL)
{
printf("NULL ");
return;
}
InOrder(root->left);
printf("%c ", root->data);
InOrder(root->right);
}
//Post order
void PostOrder(BTNode*root)
{
if (root == NULL)
{
printf("NULL ");
return;
}
PostOrder(root->left);
PostOrder(root->right);
printf("%c ", root->data);
}
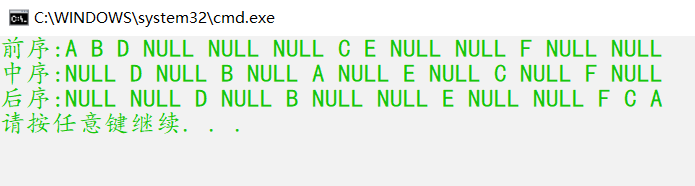
int main()
{
BTNode*root = CreatBinaryTree();
printf("Preamble:");
PreOrder(root);
printf("\n Middle order:");
InOrder(root);
printf("\n Post order:");
PostOrder(root);
printf("\n");
return 0;
}
Sequence traversal:
Let the number of layers of the root node of the binary tree be 1. Sequence traversal is to start from the root node of the binary tree, first access the root node of the first layer, then access the nodes on the second layer from left to right, then the nodes on the third layer, and so on. The process of accessing the nodes of the tree layer by layer from top to bottom and from left to right is sequence traversal, It just conforms to the queue characteristics, so it can be implemented with queue
As shown in the following figure, the result of sequence traversal: A B C D E F (NULL skipping encountered)
code:
Note: Queue.h and queue. C are required here (there are queue implementation codes in them). Take the articles about partners to the stack and queue. Queue.h needs to be slightly modified, as shown in the figure below
//Queue for sequence traversal
typedef char BTDataType;
typedef struct BinaryTreeNode
{
struct BinaryTreeNode*left;
struct BinaryTreeNode*right;
BTDataType data;
}BTNode;
void LevelOrder(BTNode* root)
{
if (root == NULL)
return false;
Queue q;
QueueInit(&q);
QueuePush(&q, root);
while (!QueueEmpty(&q))
{
BTNode*front = QueueFront(&q);
QueuePop(&q);
printf("%c ", front->data);
//Bring the children into the queue
if (front->left)
QueuePush(&q, front->left);
if (front->right)
QueuePush(&q, front->right);
}
printf("\n");
QueueDestroy(&q);
}Remember to create a binary tree during code detection, as in the preceding, middle and subsequent code segments
4.2 function realization of binary tree
// Number of binary tree nodes int BinaryTreeSize(BTNode* root); // Number of leaf nodes of binary tree int BinaryTreeLeafSize(BTNode* root); // Number of nodes in the k-th layer of binary tree int BinaryTreeLevelKSize(BTNode* root, int k); // The binary tree looks for a node with a value of x BTNode* BinaryTreeFind(BTNode* root, BTDataType x); //Depth / height of binary tree int BinaryTreeDepth(BTNode* root); // Binary tree destruction void BinaryTreeDestory(BTNode** root); // Judge whether the binary tree is a complete binary tree bool BinaryTreeComplete(BTNode* root);
Code implementation:
//Number of binary tree nodes
//void BinaryTreeSize(BTNode* root, int*pn)
//{
//
// if (root == NULL)
// return;
// ++(*pn);
// BinaryTreeSize(root->left,pn);
// BinaryTreeSize(root->right,pn);
//
//}
int BinaryTreeSize(BTNode* root)
{
if (root == NULL)
return 0;
return BinaryTreeSize(root->left) +
BinaryTreeSize(root->right) + 1;
}
Number of leaf nodes of binary tree
int BinaryTreeLeafSize(BTNode*root)
{
if (root == NULL)
return 0;
if (root->left == NULL&&root->right == NULL)
return 1;
return BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right);
}
The second of binary tree k Number of layer nodes
int BinaryTreeLeveKSize(BTNode*root, int k)
{
assert(k >= 1);
if (root == NULL)
return 0;
if (k == 1)
return 1;
//Root is not empty and K is not 1, indicating that the k layer is in the subtree of root
//Then take the left and right subtrees of root as roots, and the original K for root becomes k-1 for the left and right subtrees
//(k for root and k-1 for root's subtree)
return BinaryTreeLeveKSize(root->left,k-1) + BinaryTreeLeveKSize(root->right,k-1);
}
Depth of binary tree/height
int BinaryTreeDepth(BTNode* root)
{
if (root == NULL)
return 0;
//Find the depth of the left and right subtrees, and then return the maximum + 1
int left = BinaryTreeDepth(root->left);
int right = BinaryTreeDepth(root->right);
return left > right ? left + 1 : right + 1;
}
//The binary tree looks for a node with a value of x
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{
if (root == NULL)
return NULL;
if (root->data == x)
return root;
//Look left and then right
BTNode*left = BinaryTreeFind(root->left, x);
if (left)
return left;
BTNode*right = BinaryTreeFind(root->right, x);
if (right)
return right;
//I didn't find it
return NULL;
}
// Binary tree destruction
void BinaryTreeDestory(BTNode** root)
{
if (*root == NULL)
return;
BinaryTreeDestory((*root)->left);
BinaryTreeDestory((*root)->right);
free(root);
*root = NULL;
}
//Judge whether the binary tree is a complete binary tree
bool BinaryTreeComplete(BTNode* root)
{
//With the idea of sequence traversal, the non empty nodes of a complete binary tree are continuous whether they are empty or not
//The non empty nodes of an incomplete binary tree are not continuous
Queue q;
QueueInit(&q);
QueuePush(&q, root);
while (!QueueEmpty(&q))
{
BTNode*front = QueueFront(&q);
QueuePop(&q);
if (front == NULL)
break;
else
{
QueuePush(&q, front->left);
QueuePush(&q, front->right);
}
}
//When empty is encountered, check the remaining nodes in the queue
//1. If the rest are empty, it is a complete binary tree
//2. If there are non empty nodes in the rest, it is not a complete binary tree
while (!QueueEmpty(&q))
{
BTNode*front = QueueFront(&q);
QueuePop(&q);
if (front)
return false;
}
QueueDestroy(&q);
return true;
}