[data structure] - binary sort tree

In the last article, we described in detail a more common and efficient search algorithm in linear table - half search, but if we encounter a dynamic lookup table when we want to insert and delete data, how should we implement it?
This leads to the concept of binary sort tree. It can not only make the insertion and deletion efficient, but also realize the search more efficiently. This article will have a good understanding of it~

1, What is binary sort tree

Binary sort tree is also called binary search tree. It is either an empty tree or a binary tree with the following properties:

If its left subtree is not empty, the values of all nodes on the left subtree are smaller than the values of its root nodes
If his right subtree is not empty, the values of all nodes on the right subtree are greater than the values of his root nodes
His left and right subtrees are also binary sorting trees
As shown in the picture: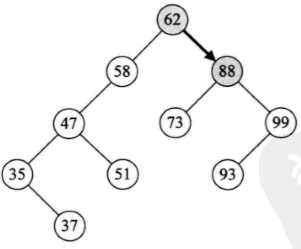

Objective: to improve the speed of searching and inserting delete keywords.

2, Search operation of binary sort tree

First, the structure of a binary tree is provided

typedef struct BiTNode
{
    int data;
    struct BiTNode *lchild,*rchild;
}BiTNode,*BiTree;

Implementation of searching binary sort tree

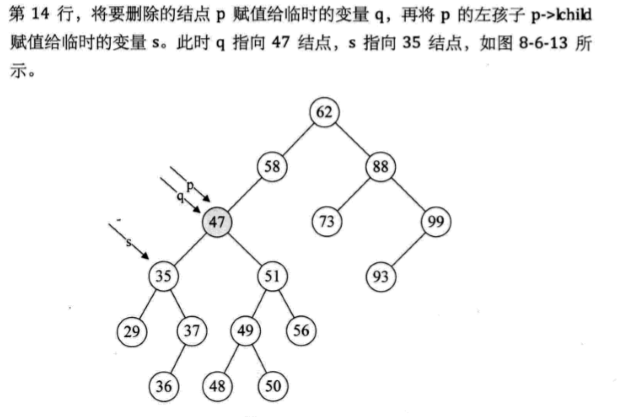
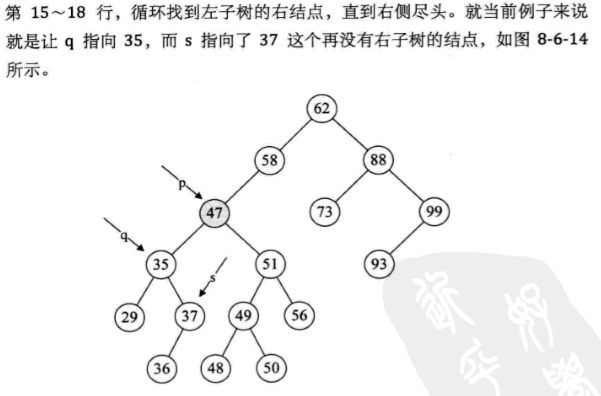
//Pointer f points to the parent of T and its initial call value is NULL
//If the search is successful, the pointer p points to the data element node and returns TRUE
//Otherwise, the pointer p points to the last node accessed on the lookup path and returns false
Status SearchBST(BiTree T,int key,BiTree f,BiTree *P)
{
    if(!T)
    {
        *p = f;
        return fales;
    }
    else if( key == T->data)
    {
        *p =T;
        return true;
    }
    else if(key < T>data)
        return SearchBST(T>lchid,key,T,p);//Continue searching in the left subtree
    else
        return SearchBST(T>rchid,key,T,p);//Continue searching in the right subtree
}

Algorithm analysis:
SearchBST function is a recursive function. f points to the parents of T. when t points to the root node, the initial value of f is NULL.

3, Insert operation of binary tree

Status InsertBST(BiTree *T,int key)
{
    BiTree p,s;
    if(!SearchBST(*T,key,ULL,&p))//If the search is not successful
    {
        s = (BiTree)malloc(sizeof(BiTNode));
        s->data = key;
        s->lchild = s->rchild = NULL;
        if(!p)
            *T = s;//Insert s as the new root node
        else if(key < p->data)
            p->lchid = s;//Insert s as left child
        else
            p->rchild = s;
    }
    else
        return false;
}

With the above insert operation, we can use it to create a binary tree

int i;
int a[10] = {62,88,58,47,35,73,51,99,37,93};
BiTree T = NULL;
for(i=0;i<10;i++)
{
    InsertBST(&T,a[i]);
}

Deleting binary tree

There are three situations:
1. Delete the leaf node: directly delete it, and it has no effect on the whole tree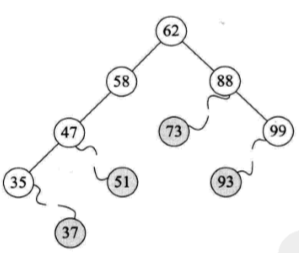

2. When there is only left subtree or only right subtree in the deleted node, the whole left subtree or right subtree of the deleted node can be moved to the location of the deleted node.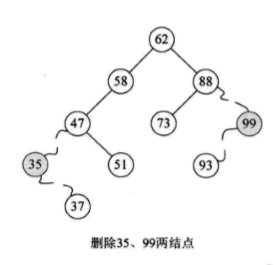

3. The deleted node has both left and right subtrees: find the direct precursor (or direct successor) s to delete node p, replace node p with s, and then delete this node s

Code implementation:
First find the node to delete in the binary tree

Status DeleteBST(BiTree *T,int key)
{
    if(!*T)//No data element with key
        return false;
    else
    {
        if(key == (*T)->data)
            return Delete(T);
        else if(key < (*T)->data)
            return DeleteBST(&(*T)->lchid,key);
         else
            return DeleteBST(&(*T)->lchid,key);
     }
 }

Implementation of Delete function

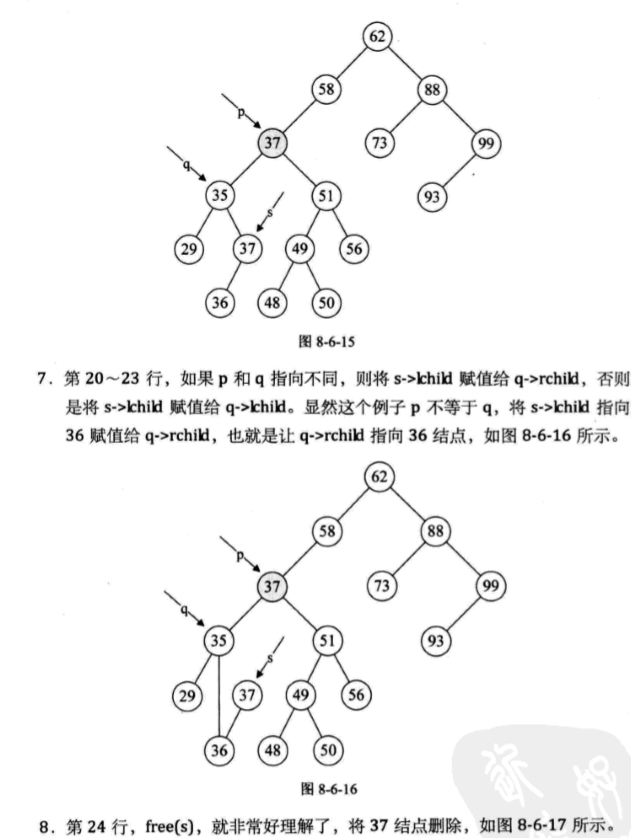
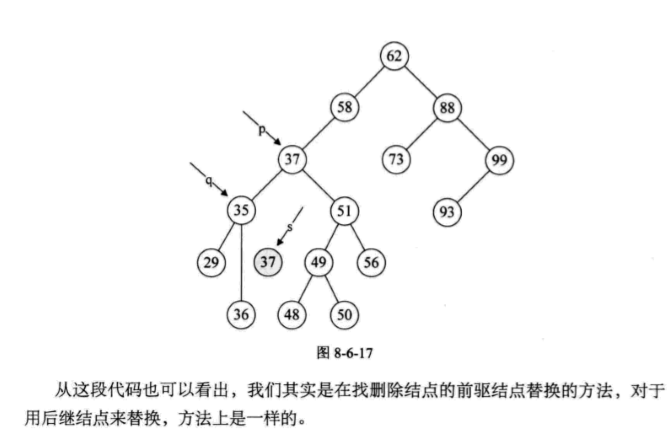
Status Delete(BiTree* p)
{
    BiTree q,s;
    if((*p)->rchild = NULL)//If the right subtree is empty, the left subtree should be reconnected
    {
        q = *p;
        *p = (*p)->lchid;
        free(q);
    }
    else if((*p)->lchild = NULL)//If the left subtree is empty, you need to reconnect its right subtree
    {
        q = *p;
        *p = (*p)->rchid;
        free(q);
    }
    else//Left and right subtrees are not empty
    {
        q = *p;
        s = (*p)->lchid;
        while(s->rchild)
        {
            q=s;
            s=s->child;
        }//q is always the last node s passed by
        (*p)->data = s->data;
        if(q != *p)
            q->rchild = s->lchid;
        else
            q->lchid = s->lchid;
        free(s);
    }
    return ture;
}