introduce

Binary search tree is a special form of binary tree. The binary search tree has the following properties: the value in each node must be greater than (or equal to) any value in its left subtree, but less than (or equal to) any value in its right subtree.

In this chapter, we will introduce the definition of binary search tree in more detail, and provide some exercises related to binary search tree.

After completing this card, you will:

1. Understanding the Properties of Binary Search Trees
2. Familiar with basic operations in binary search tree
3. Understanding the concept of highly balanced binary search tree

Definition of Binary Search Tree

Binary search tree (BST) is a special representation of binary tree. It satisfies the following characteristics:

1. The value in each node must be greater than (or equal to) any value stored in its left subtree.
2. The value in each node must be less than (or equal to) any value stored in its right subtree.

Here is an example of a binary search tree:

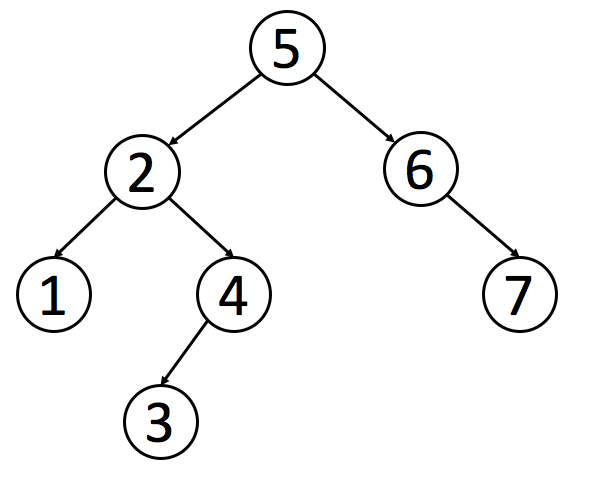
After this article, we provide a problem to verify whether a tree is a binary search tree. You can judge by the nature we mentioned above. The idea of recursion introduced in the previous chapter may also help you solve this problem.

Like ordinary binary trees, we can traverse a binary search tree in order of precedence, middle order and postorder. However, it is worth noting that for binary search trees, we can obtain an incremental ordered sequence by mid-order traversal. Therefore, mid-order traversal is the most commonly used traversal method in binary search tree.

In the article exercises, we also added the topic that lets you solve in-order successor of binary search tree. Obviously, you can find the sequential successor nodes of the binary search tree by means of intermediate traversal. You can also try to use the characteristics of binary search tree to find better solutions.

Verify Binary Search Tree

Given a binary tree, it is judged whether it is an effective binary search tree.

Suppose a binary search tree has the following characteristics:

• The left subtree of a node contains only fewer than the current number of nodes.
• The right subtree of a node contains only more than the number of current nodes.
• All left subtrees and right subtrees themselves must also be binary search trees.

Example 1:

Input:
    2
   / \
  1   3
 Output: true

Example 2:

Input:
    5
   / \
  1   4
     / \
    3   6
 Output: false
 Interpretation: The input is: [5,1,4,null,null,3,6].
     The root node has a value of 5, but its right child node has a value of 4.

Reference resources: https://www.cnblogs.com/grandyang/p/4298435.html

#include <iostream>
#include <vector>

using namespace std;

class TreeNode{
public: 
    int val;
    TreeNode* left;
    TreeNode* right;
    TreeNode(){};
    TreeNode(int x):val(x), left(NULL), right(NULL){};
};

// Recursion without inorder traversal
//This validation binary search tree has many kinds of solutions, which can be done by its own nature, that is, left < root < right, or by using the intermediate traversal resu lt as an ordered sequence. Now let's first look at the simplest one, which is to use its own nature to do it. Initialization brings in the maximum and minimum values of the system, and in the recursion. In order to include the boundary condition of int, long replaces int by their own node values in the process of return. The code is as follows:
class SolutionA{
public:
    bool isValidBST(TreeNode* root){
        return isValidBST(root, LONG_MIN, LONG_MAX);
    }
    bool isValidBST(TreeNode* root, long mn, long mx){
        if(!root) return true;
        if(root->val <= mn || root->val >= mx) return false;
        return isValidBST(root->left, mn, root->val) && isValid(root->right, root->val, mx);
    }
};
//Recursion
//This problem actually simplifies the difficu lt y, because sometimes the binary search tree in the title is defined as left <= root < right, and this question is set as left < root < right in general, then it can be done by middle order traversal. Because if the condition of left = root is not removed, the lower two numbers can not be distinguished by traversing in middle order:
class SolutionB{
public: 
    bool isValidBST(TreeNode* root){
        if(!root) return true;
        vector<int> vals;
        inorder(root, vals);
        for(int i=0; i<vals.size()-1; i++){
            if(vals[i] >= vals[i+1]) return false;
        }
        return true;
    }
    void inorder(TreeNode* root, vector<int>& vals){
        if(!root) return;
        inorder(root->left, vals);
        vals.push_back(root->val);
        inorder(root->right, vals);
    }
};

Binary Search Tree Iterator

Implement a binary search tree iterator. You will initialize the iterator using the root node of the binary search tree.

Calling next() returns the next smallest number in the binary search tree.

Examples:

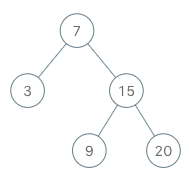
BSTIterator iterator = new BSTIterator(root);
iterator.next();    // Return 3
iterator.next();    // Return 7
iterator.hasNext(); // Return true
iterator.next();    // Return 9
iterator.hasNext(); // Return true
iterator.next();    // Return to 15
iterator.hasNext(); // Return true
iterator.next();    // Return to 20
iterator.hasNext(); // Return false

Tips:

• The time complexity of next() and hasNext() operations is O(1), and O(h) memory is used, where h is the height of the tree.
• You can assume that next() calls are always valid, that is, when next() is called, there is at least one next smallest number in BST.

Reference resources: https://www.cnblogs.com/grandyang/p/4231455.html

#include <iostream>
#include <stack>

using namespace std;

class TreeNode{
public: 
    int val;
    TreeNode* left;
    TreeNode* right;
    TreeNode(){};
    TreeNode(int x):val(x), left(NULL), right(NULL){};
};

class BSTIterator{
private: 
    stack<TreeNode*> s;
public: 
    BSTIterator(TreeNode* root){
        while(root){
            s.push(root);
            root = root->left;
        }
    }
    bool hasNext(){
        return !s.empty();
    }
    int next(){
        TreeNode* n = s.top();
        s.pop();
        int res = n->val;
        if(n->right){
            n = n->right;
            while(n){
                s.push(n);
                n = n->left;
            }
        }
        return res;
    }
};

int main(){
    return 0;
}

Basic operations in binary search tree

Implementation of Search Operation in Binary Search Tree

The binary search tree mainly supports three operations: search, insert and delete. In this chapter, we will discuss how to search for specific values in a binary search tree.

According to the characteristics of BST, for each node:

1. If the target value equals the value of the node, the node is returned.
2. If the target value is less than the value of the node, then continue to search in the left subtree.
3. If the target value is greater than the node value, continue to search in the right subtree.

Let's look at an example: we search for nodes with a target value of 4 in the binary search tree above.

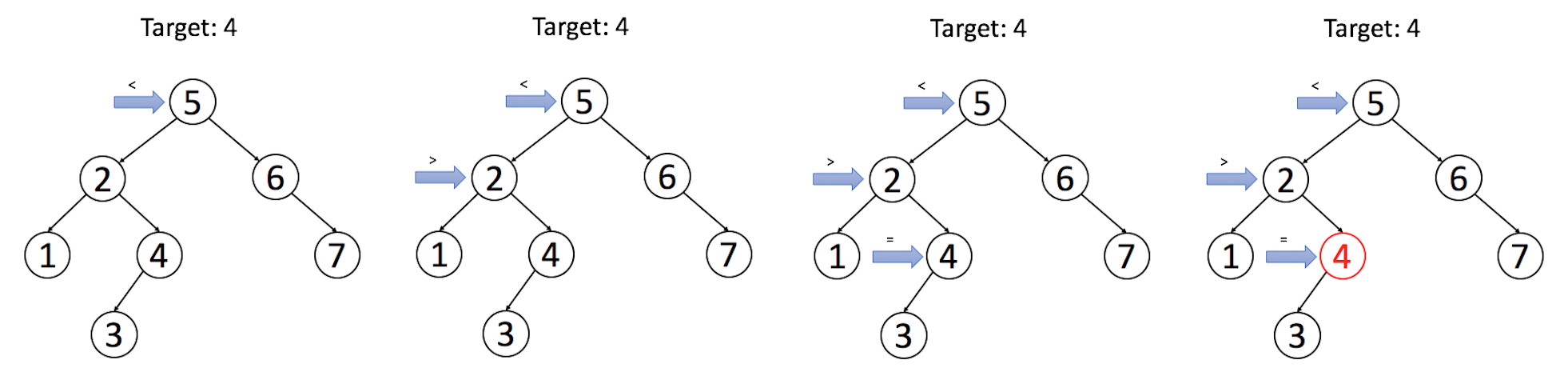
Please try to implement the search operation in the following exercises. You can use recursive or iterative methods to solve these problems, and try to analyze the time complexity and space complexity. We will introduce a better solution in a later article.

Search in a Binary Search Tree

Given the root node and a value of the binary search tree (BST). You need to find a node in BST whose value is equal to the given value. Returns a subtree with the node as its root. If the node does not exist, NULL is returned.

For example,

Given a binary search tree:

        4
       / \
      2   7
     / \
    1   3

Sum value: 2

You should return to the following subtree:

      2     
     / \   
    1   3

In the above example, if the value to be found is 5, but because there is no node value of 5, we should return NULL.

Reference resources https://www.cnblogs.com/grandyang/p/9912434.html

#include <iostream>

using namespace std;

class TreeNode{
public: 
    int val;
    TreeNode* left;
    TreeNode* right;
    TreeNode(){};
    TreeNode(int n):val(x),left(NULL),right(NULL);
};

//Recursion
class SolutionA{
public: 
    TreeNode* searchBST(TreeNode* root, int val){
        if(!root) return NULL;
        if(root->val == val) return root;
        return (root->val > val)? searchBST(root->left, val):searchBST(root->right, val);
    }
};

//Non-recursion
class SolutionB{
public: 
    TreeNode* searchBST(TreeNode* root, int val){
        while(root && root->val != val){
            root = (root->val > val)? root->left:root->right;
        }
        return root;
    }
};

Implementing Insertion in Binary Search Tree-Introduction

Another common operation in a binary search tree is inserting a new node. There are many different ways to insert new nodes. In this article, we only discuss a classical way to minimize the overall operation changes. Its main idea is to find the appropriate leaf node location for the target node, and then insert the node as the leaf node. Therefore, search will be the beginning of insertion.

Similar to the search operation, for each node, we will:

1. According to the relationship between the node value and the target node value, the left subtree or the right subtree are searched.
2. Repeat step 1 until the external node is reached.
3. According to the relationship between the value of the node and the value of the target node, the new node is added to its left or right sub-node.

In this way, we can add a new node and still maintain the nature of the binary search tree.

Let's take an example:

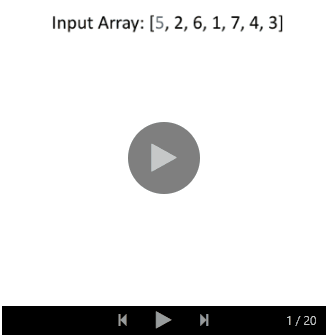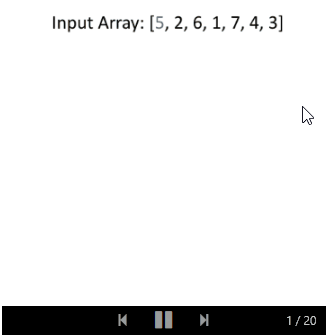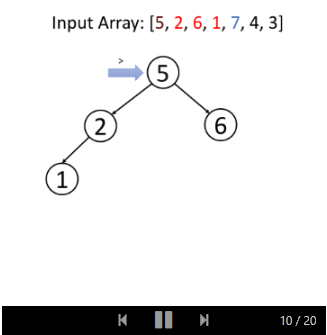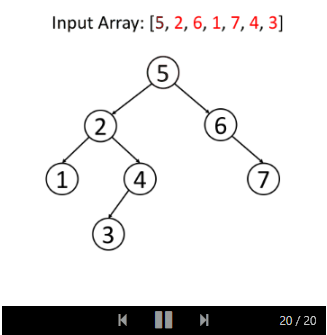
As with the search operation, we can insert it recursively or iteratively. Its solution is very similar to search. You should be able to implement it yourself and analyze the time and space complexity of the algorithm in the same way.

Insert into a Binary Search Tree

Given the root node of the binary search tree (BST) and the value to be inserted into the tree, the value is inserted into the binary search tree. Returns the root node of the inserted binary search tree. Guarantee that there are no new values in the original binary search tree.

Note that there may be many effective insertion methods, as long as the tree remains a binary search tree after insertion. You can return any valid result.

For example,

Given a binary search tree:

        4
       / \
      2   7
     / \
    1   3

And insert values: 5

You can return to this binary search tree:

         4
       /   \
      2     7
     / \   /
    1   3 5

Or the tree is valid:

         5
       /   \
      2     7
     / \   
    1   3
         \
          4

#include <iostream>

using namespace std;

class TreeNode{
public: 
    int val;
    TreeNode* left;
    TreeNode* right;
    TreeNode(){};
    TreeNode(int n):val(n),left(NULL),right(NULL){};
};

//Recursion
class SolutionA{
public: 
    TreeNode* insertIntoBST(TreeNode* root, int val){
        if(!root) return new TreeNode(val);
        if(root->val > val) root->left = insertIntoBST(root->left, val);
        else root->right = insertIntoBST(root->right, val);
        return root;
    }
};

//Non-Recursion
class SolutionB{
public: 
    TreeNode* insertIntoBST(TreeNode* root, int val){
        if(!root) return new TreeNode(val);
        TreeNode* cur = root;
        while(true){
            if(cur->val > val){
                if(!cur->left) {cur->left = new TreeNode(val); break;
                cur = cur->left;}
            }else{
                if(!cur->right) {cur->right=new TreeNode(val); break;
                cur = cur->right;}
            }
        }
        return root;
    }
};

Implementing Delete Operation in Binary Search Tree

Deletion is much more complex than the two operations we mentioned earlier. There are many different ways to delete nodes. In this article, we will discuss only one way to minimize the overall operation changes. Our solution is to replace the target node with an appropriate child node. According to the number of its sub-nodes, we need to consider the following three situations:

1. If the target node has no child nodes, we can remove the target node directly.
2. If the target section has only one child node, we can replace it with its child nodes.
3. If the target node has two sub-nodes, we need to replace them with sequential successor nodes or precursor nodes, and then delete the target node.

Let's look at the following examples to help you understand the central idea of deletion:

Example 1: The target node has no child nodes

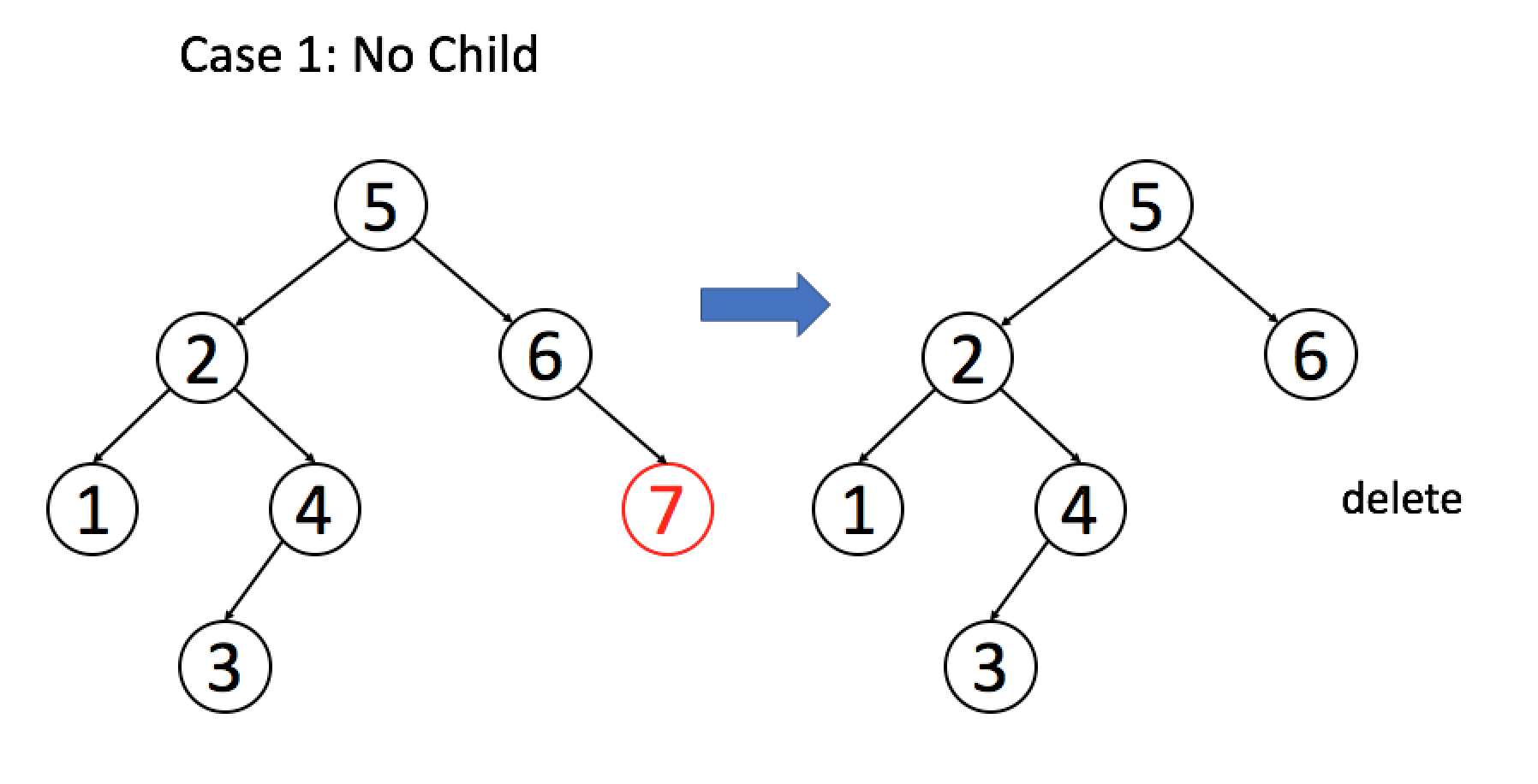
Example 2: The target section has only one child node

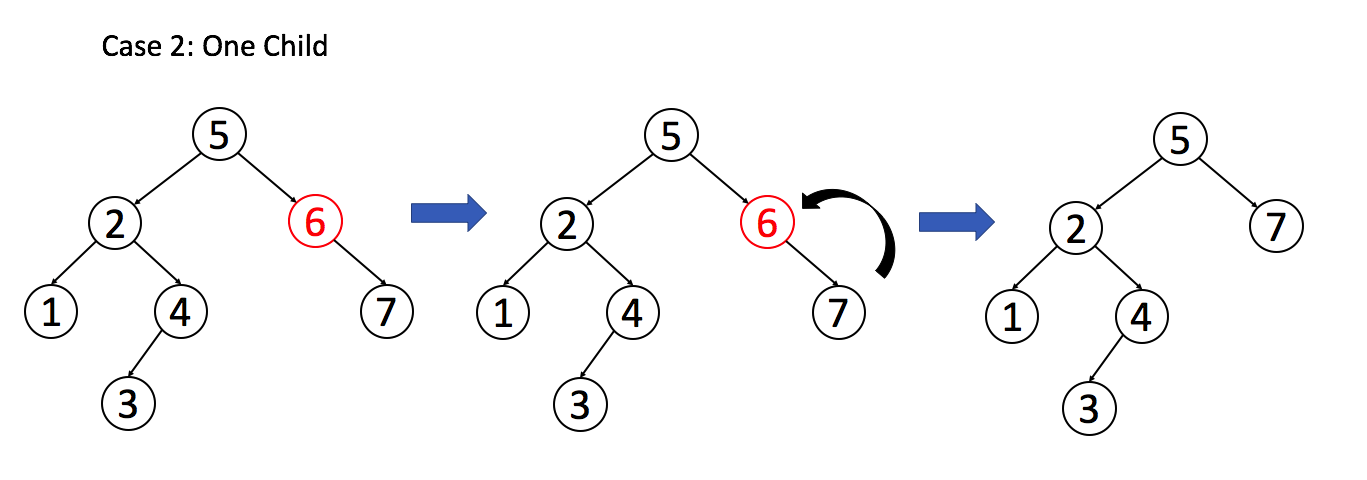
Example 3: The target node has two sub-nodes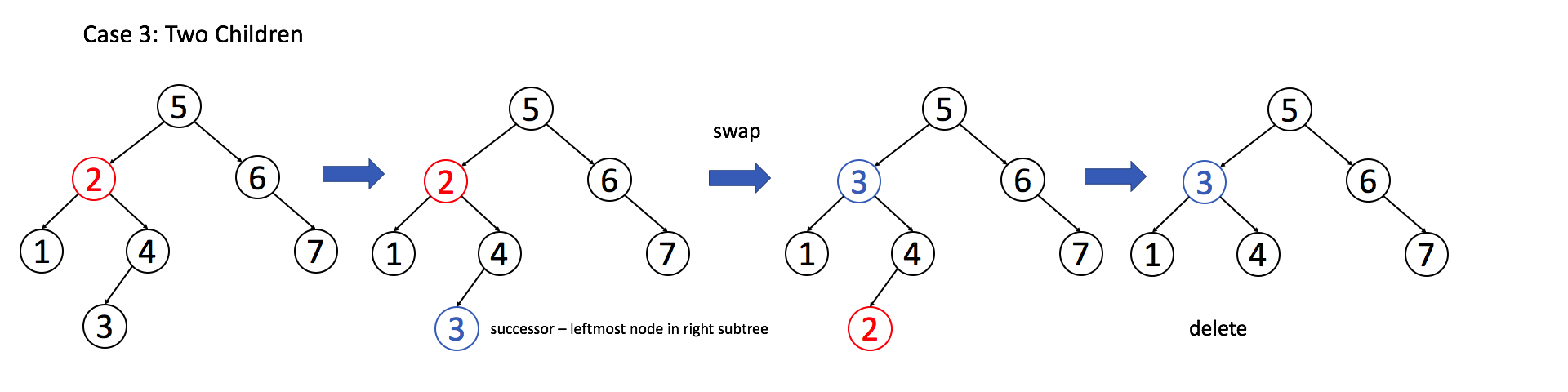

By understanding the examples above, you should be able to implement the deletion operation independently.

Delete Node in a BST

Given a root node and a value key of a binary search tree, the nodes corresponding to the key in the binary search tree are deleted, and the properties of the binary search tree are guaranteed unchanged. Returns a reference to the root node of the binary search tree, which may be updated.

Generally speaking, deleting nodes can be divided into two steps:

1. Firstly, the nodes that need to be deleted are found.
2. If found, delete it.

Explanation: The time complexity of the algorithm is O(h) and the height of the tree is h.

Examples:

root = [5,3,6,2,4,null,7]
key = 3

    5
   / \
  3   6
 / \   \
2   4   7

Given that the value of the node to be deleted is 3, we first find the 3 node, and then delete it.

The correct answer is [5,4,6,2,null,null,7], as shown in the figure below.

    5
   / \
  4   6
 /     \
2       7

Another correct answer is [5,2,6,null,4,null,7].

    5
   / \
  2   6
   \   \
    4   7

Reference resources https://www.cnblogs.com/grandyang/p/6228252.html

#include <iostream>

using namespace std;

class TreeNode{
public: 
    int val;
    TreeNode* left;
    TreeNode* right;
    TreeNode(){};
    TreeNode(int n):val(n),left(NULL),right(NULL){};
};

//Recursion
//Let's first look at a recursive solution, which first determines whether the root node is empty. Because of the left < root < right nature of BST, we can quickly locate the node to be deleted. For the case that the current node value is not equal to the key, we call recursive functions on its left and right sub-nodes according to the size relationship. If the current node is the node to delete, we first determine whether there is a child node does not exist, then we will point root to another node, if the left and right child nodes do not exist, then the root assignment is empty, and it is correct. The difficu lt y lies in dealing with the situation that both left and right sub-trees exist. We need to find the minimum value in the right sub-tree, that is, the lower-left node in the right sub-tree, then assign the minimum value to root, and then call the recursive function in the right sub-tree to delete the node with the minimum value. See the code below.
class SolutionA{
public: 
    TreeNode* deleteNode(TreeNode* root, int key){
        if(!root) return NULL;
        if(root->val > key){
            root->left = deleteNode(root->left, key);
        }else if(root->val < key){
            root->right = deleteNode(root->right, key);
        }else{  //Find the node to be deleted
            if(!root->left || !root->right){    //Case 1 & Case 2
                root = (root->left)? root->left : root->right;
            }else{//Go right once and then left down to find a node slightly larger than root
                TreeNode* cur = root->right;
                while(cur->left) cur = cur->left;
                root->val = cur->val;
                root->right = deleteNode(root->right, cur->val);//Need to reorder
            }
        }
    }
};

//Let's look at the iteration, or through the nature of BST to quickly locate the node to be deleted, if not found directly back to empty. The traversal process records the node pre at the previous location. If the pre does not exist, it means that the root node is to be deleted. If the node to be deleted is in the left subtree of the pre, then the left child node of the pre is connected with the deleted node, and vice versa, the right child node of the pre is connected with the deleted node. In deletion function, if left and right sub-nodes do not exist, then return empty; if one does not exist, then we return to that existence; the difficulty is still to deal with the existence of both left and right sub-nodes, or to find the minimum value in the right sub-tree that needs to delete the node, and then assign the minimum value to be deleted. Nodes, and then to deal with the connection problem of the right subtree which may exist at the minimum value. If there is no left subtree in the right subtree of the node to be deleted, then the right subtree of the minimum value can be directly connected to the right subtree of the node to be deleted (because at this time the value of the node to be deleted has been replaced by the minimum value. So now it's really about deleting the minimum node. Otherwise, we connect the right subtree of the minimum node to the left subtree of its parent node. Word expression is really around, please take your own examples step by step observation will be very clear, see the code as follows:
class SolutionB {
public:
    TreeNode* deleteNode(TreeNode* root, int key) {
        TreeNode *cur = root, *pre = NULL;
        while (cur) {
            if (cur->val == key) break;
            pre = cur;
            if (cur->val > key) cur = cur->left;
            else cur = cur->right;
        }
        if (!cur) return root;
        if (!pre) return del(cur);
        if (pre->left && pre->left->val == key) pre->left = del(cur);
        else pre->right = del(cur);
        return root;
    }
    TreeNode* del(TreeNode* node) {
        if (!node->left && !node->right) return NULL;
        if (!node->left || !node->right) {
            return (node->left) ? node->left : node->right;
        }
        TreeNode *pre = node, *cur = node->right;
        while (cur->left) {
            pre = cur;
            cur = cur->left;
        }
        node->val = cur->val;
        (pre == node ? node->right : pre->left) = cur->right;
        return node;
    }
};

//Let's look at a general solution for binary trees, which applies to all binary trees, so instead of taking advantage of the BST nature, we traverse all nodes and delete the nodes with the same key value. See the code below:
class SolutionC{
public: 
    TreeNode* deleteNode(TreeNode* root, int key){
        if(!root) return NULL;
        if(root->val == key){
            if(!root->right) return root->left;
            else{
                TreeNode* cur = root->right;
                while(cur->left) cur = cur->left;
                swap(root->val, cur->val);
            }
        }
        root->left = deleteNode(root->left, key);
        root->right = deleteNode(root->right, key);
        return root;
    }
};

Summary

A Brief Introduction to Binary Search Tree-Summary

We have introduced the characteristics of binary search tree and how to implement some basic operations in binary search tree, such as search, insert and delete. Familiar with these basic concepts, I believe you can successfully use them to solve the binary search tree problem.

The advantage of binary search tree is that even in the worst case, it allows you to perform all search, insert and delete operations within O(h) time complexity.

Generally speaking, binary search tree is a good choice if you want to store data orderly or need to perform search, insert and delete at the same time.

An example

One obvious solution is to descend the array and return the number k in the array.

But the disadvantage of this method is that in order to perform the search operation in O(1) time, each insertion of a new value needs to rearrange the position of the elements. Thus, the average time complexity of the interpolation operation becomes O(N). Therefore, the total time complexity of the algorithm will become O(N^2).

Since we need both insert and search operations, why not consider using a binary search tree structure to store data?

We know that for every node of a binary search tree, the value of all nodes in its left subtree is less than that of its root node, and the value of all nodes in its right subtree is greater than that of its root node.

In other words, for each node of the binary search tree, if its left subtree has m nodes, then the node is the m + 1 value in the ordered array that makes up the binary search tree.

You can think about it independently first. First try to store multiple nodes in the tree. You may also need to place a counter in each node to calculate how many nodes are in the subtree rooted by that node.

If you still don't understand the idea of the solution, we will provide an example animation:

1. insert

1. search

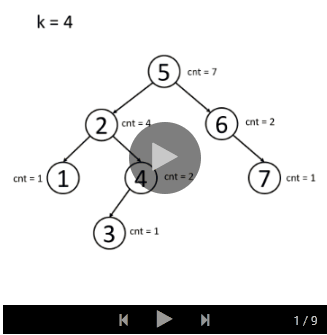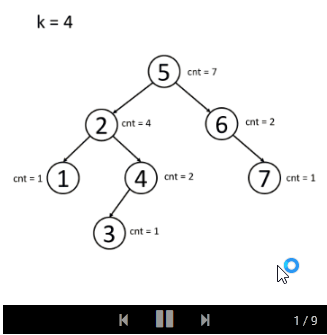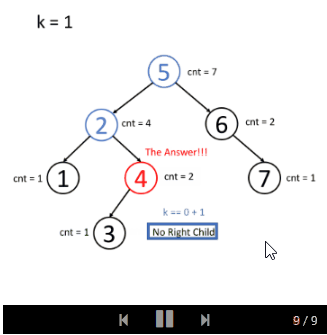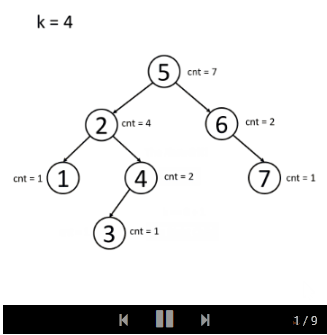
Kth Largest Element in a Stream

Design a class that finds the K largest element in the data stream. Note that this is the K largest element after sorting, not the K different element.

Your KthLargest class needs a constructor that receives both integer k and integer array nums, which contains the initial elements in the data stream. Each call to KthLargest.add returns the element with the largest K in the current data stream.

Explain:
You can assume that the length of nums is greater than k-1 and K is greater than 1.

Reference resources: https://www.cnblogs.com/grandyang/p/9941357.html

#include <iostream>
#include <queue>
#include <vector>

using namespace std;

//This problem lets us find the K largest element in the data stream, which is very similar to the previous Kth Largest Element in an Array, but the difference is that the array of the problem is determined, no more elements will be added, so it is relatively simple to determine the K largest number. And the array of this problem is constantly growing, so every time the number of the largest K is constantly changing. So we only care about the big number of the first K, so we can use a minimum heap to save the first K numbers. When new numbers are added, the minimum heap will sort automatically, and then remove the smallest number after sorting, then the heap is still a K number. When returned, we only need to return to the top element that is. Yes, see the code below:
class KthLargest{
private:
    //Priority queues are used, greater from small to large, less er from large to small.
    priority_queue<int, vector<int>, greater<int>> q;
    int K;
public: 
    KthLargest(int k, vector<int> nums){
        for(int num: nums){
            q.push(num);
            //Drop small numbers, because small numbers can only appear at >= k after inserting new numbers.
            //If a large number is inserted, the smallest number can be discarded because it will no longer be indexed to
            if(q.size() > k) q.pop();
        }
        K = k;
    }
    int add(int val){
        q.push(val);
        if(q.size() > K) q.pop();
        //Because the priority queue is placed from small to large, the element with the largest k is equivalent to choosing the smallest of the largest k.
        return q.top(); 
    }
};

Recent Common Ancestors of Binary Search Trees

Given a binary search tree, find the closest common ancestor of two specified nodes in the tree.

Baidu Encyclopedia The most recent definition of common ancestor is: "For two nodes p and q of rooted tree T, the most recent common ancestor is expressed as a node x, satisfying that x is the ancestor of p and q and the depth of X is as deep as possible (a node can also be its own ancestor)."

For example, given the following binary search tree: root = [6,2,8,0,4,7,9,null,null,3,5]

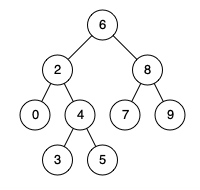
Example 1:

Input: root = 6, 2, 8, 0, 4, 7, 9, null, null, 3, 5], P = 2, q = 8
 Output: 6 
Explanation: The closest common ancestor of node 2 and node 8 is 6.

Example 2:

Input: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4
 Output: 2
 Interpretation: The nearest common ancestor of node 2 and node 4 is 2, because by definition the nearest common ancestor node can be the node itself.

Explain:

• All nodes have unique values.
• p and q are different nodes and exist in a given binary search tree.

#include <iostream>

using namespace std;

class TreeNode{
public:
    int val;
    TreeNode* left;
    TreeNode* right;
    TreeNode(){};
    TreeNode(int x):val(x),left(NULL),right(NULL){};
};

//Simplifying the Properties of Binary Search Trees
class Solution{
public: 
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q){
        //In the next process, the first person to meet p or q is the nearest ancestor.
        if(root==NULL || root==p || root==q)
            return root;
        if(p->val < root->val && q->val< root->val)
            return lowestCommonAncestor(root->left, p, q);
        else if(p->val > root->val && q->val > root->val)
            return lowestCommonAncestor(root->right, p, q);
        else    //val is one's own.
            return root;
    }
};

Existence of repetitive element III

Given an array of integers, i t is judged whether there are two different indexes I and j in the array, so that the absolute value of the difference between nums [i] and nums [j] is maximum t, and the absolute value between I and j is maximum blight.

Example 1:

Input: nums = [1,2,3,1], k = 3, t = 0
 Output: true

Example 2:

Input: nums = [1,0,1,1], k = 1, t = 2
 Output: true

Example 3:

Input: nums = [1,5,9,1,5,9], k = 2, t = 3
 Output: false

#include <iostream>
#include <vector>
#include <set>

using namespace std;

//Idea: Maintain a window of size k and move from left to right in nums. For nums[i], as long as I t finds whether there are elements with a size range of [nums[i] - t,nums[i] + t in the previous element, if there are, it returns true. Also note the overflow of integers, such as the following test cases:
class Solution {
public:
    bool containsNearbyAlmostDuplicate(vector<int>& nums, int k, int t) {
        set<long long> record;
        for(int i = 0; i < nums.size(); i++){
            //lower_bound(val) returns the location of the first element in the set greater than or equal to val. If all elements are less than val, return to last
            if(record.lower_bound((long long)nums[i] - (long long)t)  != record.end()   //Is there a number greater than nums[i] - t in record?
                   && (long long)*record.lower_bound((long long)nums[i] - (long long)t) <= (long long)nums[i] + (long long)t)   //Is there a number less than nums[i] + t in record?
                return true;

            record.insert(nums[i]);
            if(record.size() > k)
                record.erase(nums[i - k]);
        }
        return false;
    }
};

int main(){
    vector<int> v = {1,2,3,1};
    Solution a = Solution();
    if(a.containsNearbyAlmostDuplicate(v, 3, 0))
        cout << "true";
    else
        cout << "false";
}

Appendix: highly balanced binary search tree

A Brief Introduction to Highly Balanced Binary Search Tree

In this article, we will help you understand the basic concept of highly balanced binary search trees.

What is a highly balanced binary search tree?

A highly balanced binary search tree (balanced binary search tree) can automatically keep its height minimum after inserting and deleting any node. That is to say, a balanced binary search tree with N nodes is logN in height. Moreover, the height of the two subtrees of each node will not differ more than 1.

Here is an example of a general binary search tree and a highly balanced binary search tree:

By definition, we can determine whether a binary search tree is highly balanced or not.( balanced binary tree).

As we mentioned earlier, the height of a balanced binary search tree with * N * nodes is always logN. Therefore, we can calculate the total number of nodes and the height of the tree to determine whether the binary search tree is highly balanced.

Similarly, in the definition, we mention a feature of highly balanced binary trees: the depth of the two subtrees of each node does not differ by more than 1. We can also verify the tree recursively according to this property.

Why do we need a highly balanced binary search tree?

We have introduced the binary tree and its related operations, including search, insert and delete. When analyzing the time complexity of these operations, we need to note that tree height is a very important consideration. For example, if the height of the binary search tree is * h*, the time complexity is * O(h)*. The height of the binary search tree is really important.

So let's discuss the relationship between the total number of nodes N and the height * h * of the tree. For a balanced binary search tree, as we mentioned earlier, but for a common binary search tree, in the worst case, it can degenerate into a chain.

Therefore, the height of the binary search tree with N nodes varies from logN to N. That is to say, the time complexity of the search operation can change from logN to N. This is a huge performance difference.

Therefore, a highly balanced binary search tree plays an important role in improving performance.

How to achieve a highly balanced binary search tree?

There are many different ways to achieve it. Although the details of these implementations vary, they share the same goals:

1. The data structure adopted should satisfy dichotomous search attributes and highly balanced attributes.
2. The data structure adopted should support the basic operations of binary search tree, including searching, inserting and deleting in O(logN) time, even in the worst case.

We provide a common list of highly balanced binary trees for your reference.

• red-black tree
• AVL tree
• Splay Tree
• Tree Heap

We do not intend to discuss the details of the implementation of these data structures in this article.

Practical application of highly balanced binary search tree

A highly balanced binary search tree is widely used in practice because it can perform all search, insert and delete operations within O(logN) time complexity.

The concept of balanced binary search tree is often used in Set and Map. Set and Map are similar in principle. We will focus on the data structure of Set in the following sections.

Typically, there are two most widely used sets: Hash Set and Tree Set.

Tree sets, Treeset in Java or set in C++, are implemented by a highly balanced binary search tree. Therefore, the time complexity of searching, inserting and deleting is O(logN).

Hash sets, HashSet in Java or unordered_set in C++ are implemented by hashing, but balanced binary search trees also play a crucial role. When there are too many elements with the same hash key, it will take O(N) time complexity to find specific elements, where N is the number of elements with the same hash key. Usually, using a highly balanced binary search tree will improve the time complexity from O(N) to O(logN).

The essential difference between hash sets and tree sets is that the keys in tree sets are ordered.

summary

The highly balanced binary search tree is a special representation of the binary search tree, aiming at improving the performance of the binary search tree. However, the specific implementation of this data structure is beyond the content of our chapter, and seldom be examined in the interview. But it's very useful to understand the basic concepts of highly balanced binary search trees and how to use them to help you design algorithms.

balanced binary tree

Given a binary tree, judge whether it is a highly balanced binary tree.

In this paper, a height-balanced binary tree is defined as:

Example 1:

Given a binary tree [3,9,20,null,null,15,7]

    3
   / \
  9  20
    /  \
   15   7

Returns true.

Example 2:

Given a binary tree [1,2,2,3,3,null,null,4,4]

       1
      / \
     2   2
    / \
   3   3
  / \
 4   4

Return false.

Refer to https://www.cnblogs.com/simplekinght/p/9219697.html.

class Solution{
public:
    int judge(TreeNode* root, bool &ans){
        if(root){
            int ans1 = judge(root->left, ans);
            int ans2 = judge(root->right, ans);
            if(abs(ans1-ans2)>1) ans=false;
            return max(ans1, ans2) + 1;
        }
        else return 0;
    }
    bool isBalanced(TreeNode* root){
        bool ans = true;
        judge(root, ans);
        return ans;
    }
};

Converting Ordered Arrays to Binary Search Trees

An ordered array arranged in ascending order is transformed into a highly balanced binary search tree.

In this problem, a highly balanced binary tree means that the absolute value of the height difference between the left and right subtrees of each node of a binary tree does not exceed 1.

Examples:

Given an ordered array: [-10, -3, 0, 5, 9],

One possible answer is: [0,-3,9,-10,null,5], which can represent the following highly balanced binary search tree:

      0
     / \
   -3   9
   /   /
 -10  5

Refer to https://www.cnblogs.com/grandyang/p/4295618.html

#include <iostream>
#include <vector>

using namespace std;

class TreeNode{
public: 
    int val;
    TreeNode* left;
    TreeNode* right;
    TreeNode(){};
    TreeNode(int n):val(n),left(NULL),right(NULL){};
};

//This problem is to transform an ordered array into a binary search tree. The so-called binary search tree is a feature that always satisfies the left < root < right. If the binary search tree is traversed in the middle order, an ordered array will be obtained. On the other hand, we can know that the root node should be the middle point of an ordered array, which is divided into left and right ordered arrays, and find out the left and right sub-nodes of which the middle point is the original middle point, which is the core idea of the dichotomy search method. So this question is the dichotomy search method, the code is as follows:
class SolutionA{
public: 
    TreeNode* sortedArrayToBST(vector<int>& nums){
        return helper(nums, 0, (int)nums.size()-1);
    }
    TreeNode* helper(vector<int>& nums, int left, int right){
        if(left > right) return NULL;
        int mid = left + (right-left) /2 ;
        TreeNode* cur = new TreeNode(nums[mid]);
        cur->left = helper(nums, left, mid-1);
        cur->right = helper(nums, mid+1, right);
        return cur;
    }
};

//We can also complete the recursion in the original function instead of using the extra recursive function. Since the parameter of the original function is an array, when the middle number of the input array is taken out, the arrays at both ends need to be formed into a new array, and the recursive function is called separately, and connected to the newly created cur. On the left and right sub-nodes of the node, see the code below.
class SolutionB{
public: 
    TreeNode* sortedArrayToBST(vector<int>& nums){
        if(nums.empty()) return NULL;
        int mid = nums.size() / 2;
        TreeNode* cur = new TreeNode(nums[mid]);
        vector<int> left(nums.begin(), nums.begin()+mid), right(nums.begin() + mid+1, nums.end());
        cur->left = sortedArrayToBST(left);
        cur->right = sortedArrayToBST(right);
        return cur;
    }
};