Basic definition of tree
A tree is a set with hierarchical relationship composed of n (n > = 1) finite points.
Characteristics of trees
- Each node has 0 or more child nodes
- A node without a parent node is called a root node
- Each non root node has only one parent node
- Each node and its descendants can be regarded as a tree as a whole, which is called a subtree of the parent node of the current node
Related terms
- Node degree: the number of [subtrees] contained in a node is called the degree of the node
- Leaf node: a node with a degree of 0 is called a leaf node or a terminal node
- Branch node: a node whose degree is not 0 is called a branch node or a non terminal node
- Node level: starting from the root node, the level of the root node is 1, the direct successor level of the root is 2, and so on
- Sequence number of nodes: the nodes in the tree are arranged into a linear sequence from the upper layer to the lower layer and from left to right in the same layer, and they are compiled into continuous natural numbers
- Tree degree: the maximum value of all node degrees in the tree
- Height of tree: the maximum level of nodes in the tree
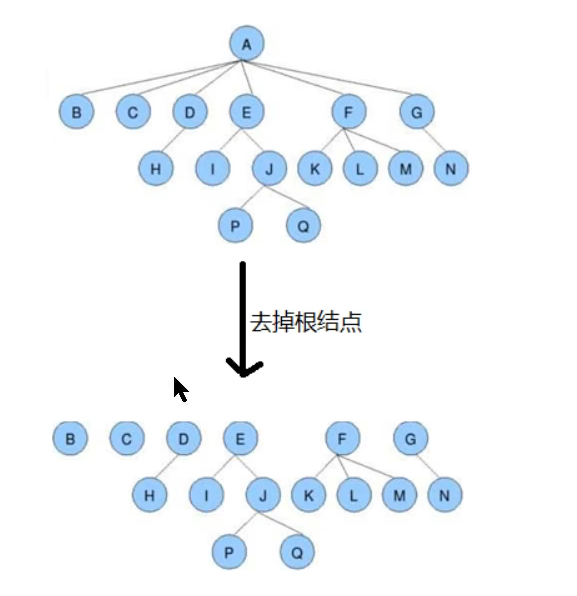
- Forest: a collection of M (M > 0) disjoint trees. If the root node of a non empty tree is deleted, the tree becomes a forest; Add a unified root node to the forest, and the forest will become a tree
- Child node: the direct successor node of a node is called the child node of the node
- Parent node: the direct precursor of a node is called the parent node (parent node) of the node
- Sibling node: child nodes of the same parent node are called sibling nodes
Binary tree
definition
A binary tree is a tree whose degree does not exceed 2
- Full binary tree: a binary tree. If the number of nodes in each layer reaches the maximum, the binary tree is a full binary tree
- Complete binary tree: a binary tree in which leaf nodes can only appear in the lowest layer and the lower layer, and the nodes of the lowest layer are concentrated in several positions on the leftmost side of the layer
Binary lookup number
Tree linked list and recursion
Add key value pair
- If the current tree species has no root node, the new node is directly used as the root node
- If the current tree is not empty, start from the root node
- If the key of the new node is less than the key of the current node, continue to find the left subtree of the current node
- If the key of the new node is greater than the key of the current node, continue to find the right subtree of the current node
- If the key of the new node is equal to the key of the current node, such a node already exists in the number. Replace the value value of the node
Find element
- If the passed in element is empty, null is returned directly
- Element is not empty. Compare the size of key and key
- If the key > element, continue to find the right subtree
- If key < element, continue to find the number of left words of the element
- If key = = element, the node with key is found. You only need to return the node value of the element
Delete element
- Find the deleted node
- Find the minimum node minNode in the right subtree of the deleted node
- Delete the smallest node in the right subtree
- Let the left subtree of the deleted node become the left subtree of the smallest node, and let the right subtree of the deleted node become the right subtree of the smallest node
- Let the parent node of the deleted node point to the minimum node minNode
code implementation
For the tree data structure, the addition, search and deletion can be realized by the tree structure. The number of layers is not deep and the number of calls is limited
Recursive elements:
- There is an exit
- Step by step
package practice;
import com.sun.jdi.Value;
public class TwoTree<Key extends Comparable<Key>,Value> {
private int N;
public Node root;
public TwoTree(){
this.root = null;
this.N = 0;
}
private class Node{
private Node left;
private Node right;
public Key key;
public Value value;
public Node(Key key, Value value, Node right, Node left ){
this.key = key;
this.value = value;
this.left = left;
this.right = right;
}
}
//Gets the number of elements in the tree
public int length(){
return N;
}
//Add elements to the tree
public void put(Key key, Value value){
root = put(root, key, value);
}
private Node put(Node x, Key key, Value value){
if (x==null){
N++;
Node newNode = new Node(key,value,null,null);
return newNode;
}else{
//If the root node is not null, compare the key values and continue to look down
//If the current key is less than the key of the current node, continue to find the left node of the current node
if (key.compareTo(x.key)<0){
x.left = put(x.left,key,value);
}else if (key.compareTo(x.key)>0){
//If the current key is greater than the key of the current node, continue to find the right node of the current node
x.right = put(x.right,key,value);
}else{
//If the current key is equal to the key of the current node, replace the value of the current node
x.value = value;
}
}
return x;
}
//Get element
public Value get(Key key){
return get(root, key);
}
private Value get(Node x, Key key){
//If the root node is empty, null is returned directly
//If the root node is not empty, compare the size of the current key with that of the current node
//If the current key is less than the key of the current node, the left subtree of the current key is found
//If the current key is greater than the key of the current node, find the right subtree of the current key
//If the current key is equal to the key of the current node, the value of the current node is returned
if (x==null) {
return null;
}
int cmp = key.compareTo(x.key);
if(cmp<0) {
return get(x.left, key); //Here, the temporary node is used when writing code
}else if(cmp>0){
return get(x.right, key);
}else{
return x.value;
}
}
}
Traversal of binary tree
- Preorder traversal
- Medium order traversal
- Subsequent traversal
package practice;
import com.sun.jdi.Value;
import java.util.ArrayList;
public class TwoTree<Key extends Comparable<Key>,Value> {
private int N;
public Node root;
public TwoTree(){
this.root = null;
this.N = 0;
}
private class Node{
private Node left;
private Node right;
public Key key;
public Value value;
public Node(Key key, Value value, Node right, Node left ){
this.key = key;
this.value = value;
this.left = left;
this.right = right;
}
}
//Get the number of tree element
public int length(){
return N;
}
//Add elements to the tree
public void put(Key key, Value value){
root = put(root, key, value);
}
private Node put(Node x, Key key, Value value){
if (x==null){
N++;
Node newNode = new Node(key,value,null,null);
return newNode;
}else{
//If the root node is not null, compare the key values and continue to look down
//If the current key is less than the key of the current node, continue to find the left node of the current node
if (key.compareTo(x.key)<0){
x.left = put(x.left,key,value);
}else if (key.compareTo(x.key)>0){
//If the current key is greater than the key of the current node, continue to find the right node of the current node
x.right = put(x.right,key,value);
}else{
//If the current key is equal to the key of the current node, replace the value of the current node
x.value = value;
}
}
return x;
}
//Get element
public Value get(Key key){
return get(root, key);
}
private Value get(Node x, Key key){
//If the root node is empty, null is returned directly
//If the root node is not empty, compare the size of the current key with that of the current node
//If the current key is less than the key of the current node, the left subtree of the current key is found
//If the current key is greater than the key of the current node, find the right subtree of the current key
//If the current key is equal to the key of the current node, the value of the current node is returned
if (x==null) {
return null;
}
int cmp = key.compareTo(x.key);
if(cmp<0) {
return get(x.left, key);
}else if(cmp>0){
return get(x.right, key);
}else{
return x.value;
}
}
//Delete elements in the tree
public Node delete(Key key){
return delete(root, key);
}
private Node delete(Node x, Key key){
//If the tree is empty, null is returned
//If it is not an empty tree, compare the size of the current key and the key of the current node to determine the value to be found
//If the current key is less than the key of the current node, the left subtree of the current key is found
//If the current key is greater than the key of the current node, find the right subtree of the current key
//If the current key is equal to the key of the current node, determine the current node as the minimum node
//Delete the smallest node in the right subtree of Min node
//Let the left subtree of the deleted node become the left subtree of the smallest node, and let the right subtree of the deleted node become the right subtree of the smallest node
//Let the parent node of the deleted node point to min node
if (x==null){
return null;
}
int cmp = key.compareTo(x.key);
if(cmp<0) {
x.left = delete(x.left, key);
}else if(cmp>0){
x.right = delete(x.right, key);
}else{
if (x.right==null){
return x.left;
}
if (x.left == null){
return x.right;
}
Node minNode = x.right;
while (minNode.left!=null){
minNode = minNode.left;
}
Node n = x.right;
while (n.left!=null){
if (n.left.left==null){
n.left = null;
}
}
minNode.left = x.left;
minNode.right = x.right;
x = minNode;
}
return x;
}
//Gets all keys in the entire tree
public ArrayList<Key> preErgodic(){
ArrayList<Key> al = new ArrayList<>();
preErgodic(root,al);
return al;
}
//Preorder traversal
public void preErgodic(Node x, ArrayList<Key> al){
if (x==null){
return;
}
//Put the key of x node into al
al.add(x.key);
//Recursively traversing the right subtree of x node
if (x.left!=null){
preErgodic(x.left,al);
}
//Recursively traversing the right subtree of x node
if (x.right!=null){
preErgodic(x.right,al);
}
}
//Medium order traversal
public ArrayList<Key> midErgodic(){
ArrayList<Key> al = new ArrayList<>();
midErgodic(root,al);
return al;
}
public void midErgodic(Node x,ArrayList al){
if (x==null){
return ;
}
//First recursion, put the keys in the left subtree into keys
if (x.left!=null){
midErgodic(x.left,al);
}
//Put the key of the current node x into al
al.add(x.key);
//Recursively, put the key in the right subtree into al
if (x.right!=null){
midErgodic(x.right,al);
}
//First recursion, put the key of the left subtree into al
}
//Use the subsequent traversal to return all the keys in the whole tree
public ArrayList<Key> afterErgodic(){
ArrayList<Key> al = new ArrayList<>();
afterErgodic(root, al);
return al;
}
public void afterErgodic(Node x, ArrayList<Key> al){
if (x==null){
return;
}
if (x.left!=null){
afterErgodic(x.left,al);
}
if (x.right!=null){
afterErgodic(x.right,al);
}
al.add(x.key);
}
}
package test;
import practice.TwoTree;
import java.util.ArrayList;
public class TwoTreeTest {
public static void main(String[] args) {
// TwoTree<Integer,String> tt = new TwoTree<>();
//
//
//
// tt.put(1, "Yao Ming");
// tt.put(2, "McGrady");
// tt.put(100, "McGrady");
// tt.put(100, "Kobe");
//
// System.out.println(tt.length());
//
// System.out.println(tt.get(100));
TwoTree<String,String> tt = new TwoTree<>();
tt.put("E","5");
tt.put("B","2");
tt.put("G","7");
tt.put("A","1");
tt.put("D","4");
tt.put("F","6");
tt.put("H","8");
tt.put("C","3");
ArrayList<String> al = tt.afterErgodic();
for (String s:al){
System.out.println(s);
}
}
}
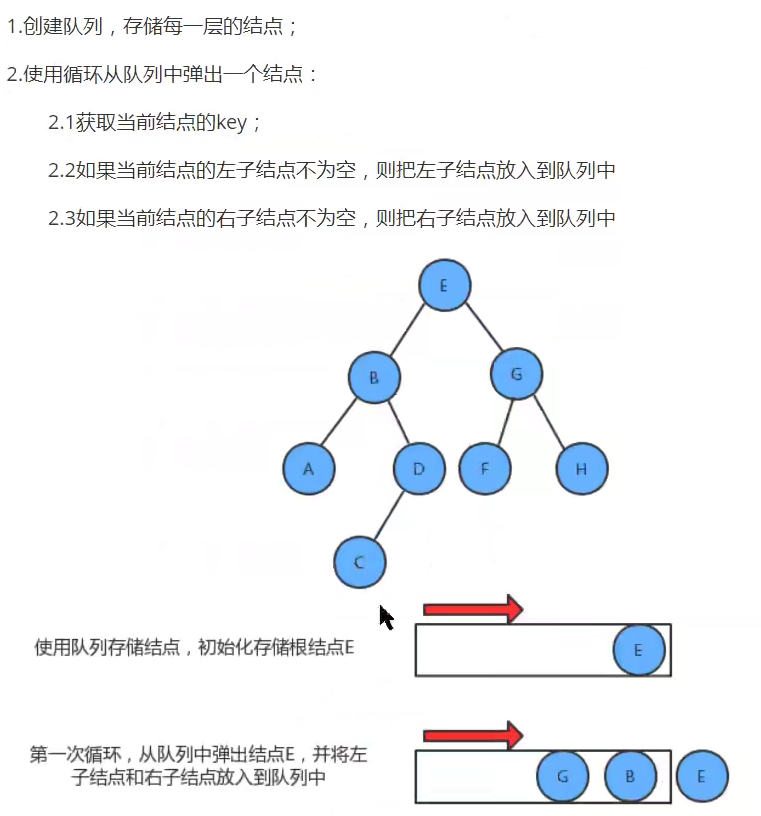
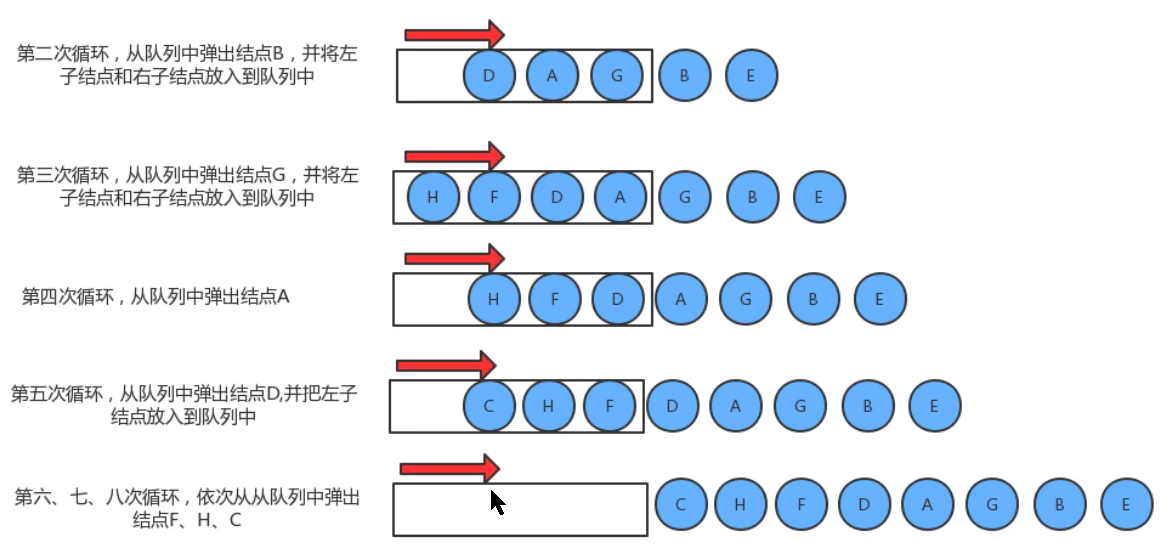
- level traversal
From top to bottom, from left to right
- Maximum depth problem
package practice;
import com.sun.jdi.Value;
import java.util.ArrayList;
import java.util.Queue;
public class TwoTree<Key extends Comparable<Key>,Value> {
private int N;
public Node root;
public TwoTree(){
this.root = null;
this.N = 0;
}
private class Node{
private Node left;
private Node right;
public Key key;
public Value value;
public Node(Key key, Value value, Node right, Node left ){
this.key = key;
this.value = value;
this.left = left;
this.right = right;
}
}
//Get the number of tree element
public int length(){
return N;
}
//Add elements to the tree
public void put(Key key, Value value){
root = put(root, key, value);
}
private Node put(Node x, Key key, Value value){
if (x==null){
N++;
Node newNode = new Node(key,value,null,null);
return newNode;
}else{
//If the root node is not null, compare the key values and continue to look down
//If the current key is less than the key of the current node, continue to find the left node of the current node
if (key.compareTo(x.key)<0){
x.left = put(x.left,key,value);
}else if (key.compareTo(x.key)>0){
//If the current key is greater than the key of the current node, continue to find the right node of the current node
x.right = put(x.right,key,value);
}else{
//If the current key is equal to the key of the current node, replace the value of the current node
x.value = value;
}
}
return x;
}
//Get element
public Value get(Key key){
return get(root, key);
}
private Value get(Node x, Key key){
//If the root node is empty, null is returned directly
//If the root node is not empty, compare the size of the current key with that of the current node
//If the current key is less than the key of the current node, the left subtree of the current key is found
//If the current key is greater than the key of the current node, find the right subtree of the current key
//If the current key is equal to the key of the current node, the value of the current node is returned
if (x==null) {
return null;
}
int cmp = key.compareTo(x.key);
if(cmp<0) {
return get(x.left, key);
}else if(cmp>0){
return get(x.right, key);
}else{
return x.value;
}
}
//Delete elements in the tree
public Node delete(Key key){
return delete(root, key);
}
private Node delete(Node x, Key key){
//If the tree is empty, null is returned
//If it is not an empty tree, compare the size of the current key and the key of the current node to determine the value to be found
//If the current key is less than the key of the current node, the left subtree of the current key is found
//If the current key is greater than the key of the current node, find the right subtree of the current key
//If the current key is equal to the key of the current node, determine the current node as the minimum node
//Delete the smallest node in the right subtree of Min node
//Let the left subtree of the deleted node become the left subtree of the smallest node, and let the right subtree of the deleted node become the right subtree of the smallest node
//Let the parent node of the deleted node point to min node
if (x==null){
return null;
}
int cmp = key.compareTo(x.key);
if(cmp<0) {
x.left = delete(x.left, key);
}else if(cmp>0){
x.right = delete(x.right, key);
}else{
if (x.right==null){
return x.left;
}
if (x.left == null){
return x.right;
}
Node minNode = x.right;
while (minNode.left!=null){
minNode = minNode.left;
}
Node n = x.right;
while (n.left!=null){
if (n.left.left==null){
n.left = null;
}
}
minNode.left = x.left;
minNode.right = x.right;
x = minNode;
}
return x;
}
//Gets all keys in the entire tree
public ArrayList<Key> preErgodic(){
ArrayList<Key> al = new ArrayList<>();
preErgodic(root,al);
return al;
}
//Preorder traversal
public void preErgodic(Node x, ArrayList<Key> al){
if (x==null){
return;
}
//Put the key of x node into al
al.add(x.key);
//Recursively traversing the right subtree of x node
if (x.left!=null){
preErgodic(x.left,al);
}
//Recursively traversing the right subtree of x node
if (x.right!=null){
preErgodic(x.right,al);
}
}
//Medium order traversal
public ArrayList<Key> midErgodic(){
ArrayList<Key> al = new ArrayList<>();
midErgodic(root,al);
return al;
}
public void midErgodic(Node x,ArrayList al){
if (x==null){
return ;
}
//First recursion, put the keys in the left subtree into keys
if (x.left!=null){
midErgodic(x.left,al);
}
//Put the key of the current node x into al
al.add(x.key);
//Recursively, put the key in the right subtree into al
if (x.right!=null){
midErgodic(x.right,al);
}
//First recursion, put the key of the left subtree into al
}
//Use the subsequent traversal to return all the keys in the whole tree
public ArrayList<Key> afterErgodic(){
ArrayList<Key> al = new ArrayList<>();
afterErgodic(root, al);
return al;
}
public void afterErgodic(Node x, ArrayList<Key> al){
if (x==null){
return;
}
if (x.left!=null){
afterErgodic(x.left,al);
}
if (x.right!=null){
afterErgodic(x.right,al);
}
al.add(x.key);
}
//Gets the maximum depth of the entire tree
public int maxDepth(){
return maxDepth(root);
}
//Gets the maximum depth of a tree
public int maxDepth(Node x){
if (x==null){
return 0;
}
int max = 0;
int maxL = 0;
int maxR = 0;
//Judge whether the left subtree is empty. If not, continue recursion
if (x.left!=null){
maxL = maxDepth(x.left);
}
//Judge whether the right subtree is empty. If not, continue recursion
if (x.right!=null){
maxR = maxDepth(x.right);
}
//Compare the maximum depth of the left subtree with the maximum depth of the right subtree, and take the larger value plus 1
max = maxL>maxR? maxL:maxR;
return max+1;
}
}