The following articles are not organized properly. Please forgive me.
Four Simple Sorting Algorithms
If you want to be an excellent developer, you should not only actively learn the popular new technologies, such as WCF, Asp.Net MVC, AJAX and so on, but also skillfully apply some mature technologies, such as Asp.Net, WinForm. It should also have solid basic knowledge of computer, such as data structure, operating system, compiling principle, network and data communication. Some friends may find this too difficult and theoretical, but I think it's not a pleasure to spend an afternoon on holiday studying an algorithm or a data structure and then writing about it. Therefore, I intend to summarize some common data structures and algorithms, not necessarily focus on a period of time and spend a lot of energy, but in a relatively leisure time with a very relaxed mind to complete. The last thing I want is to turn blogging or learning technology into a job or a burden, which should be regarded as a pastime in life. People always say that perseverance is not easy. In fact, when you mention the word "perseverance", it means that you have regarded it as a kind of pain. You are not willing to do it in your heart, so you need to persevere. You've never heard people say, "I've been playing video games for ten years," or "I've been watching animation and movies for ten years" or "I've been with my beloved girlfriend for ten years"? I never insisted, because I regarded it as a hobby and pastime, just like many people play online games.
Okay, let's talk a lot. Let's get back to the point. Because there are many works in this field, I just give a simple description and implementation here for my own reference and interested friends. I will try to use C# and C++ to achieve, for some structures that are not easy to use C# to express, only using C++ to achieve.
This article will describe four simple sorting methods, insertion sort, bubble sort, select sort, and Hill sort. I call it "simple sorting" here, because they are simpler in understanding and algorithm than in quick sort, merge sort, heap sort, distribution sort, cardinal sort. For the latter sort, I call it "advanced sort".
Simple sorting
Before starting, a convention is declared that data stored in an array is collectively referred to as records to avoid confusion with names such as "elements" and "objects". For a record, the code used for sorting is called the key code. Obviously, the choice of key code is closely related to the type of record in the array. If the record is an int value, the key code is itself; if the record is a custom object, it probably contains multiple fields, then one of these fields is selected as the key code. Every sorting and searching algorithm is related to the size of the two records, and how to determine the size of the two objects should be determined by the client (client object) of the algorithm program. For. NET, we can create a class that implements IComparer < T> (similar to C++). For more information on IComparer<T>, you can refer to this article.< Sorting Based on Business Objects " Finally, in order to make the program simple, I did not deal with the case of empty arrays.
1. Insertion sort
Algorithmic thought
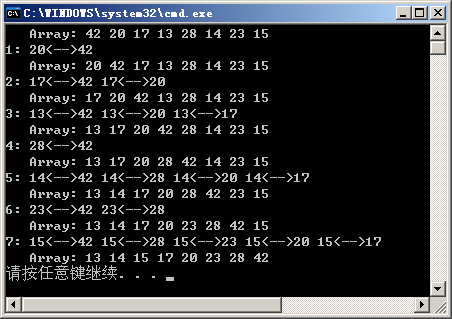
The insertion sort uses two nested loops to process the records to be sorted one by one. Each record is compared with the previously ordered sequence of records and inserted into the appropriate location. Assuming the length of the array is n, the outer loop control variable i is progressive from 1 to n-1 to select which record to process; the inner loop control variable j, whose initial value is i and decreases from i to 1, is compared with the previous record to determine which position to insert the element. The key idea here is that when dealing with Article i records, the preceding i-1 records are already in order. It should be noted that since the current record is compared with the adjacent previous record, the starting value of the loop control variable is 1 (array subscript). If the previous record is - 1, the array crosses the boundary.
Now let's look at the processing of Article i records. Assuming that the outer loop progresses to Article i records and the value of its key code is X, there may be two situations at this time:
- If the previous record is larger than X, they are exchanged until the key code of the previous record is smaller or equal to X.
- If the previous record is smaller or equal than X, then all previous records must be orderly and smaller than X, and then exit the inner loop. The outer loop moves forward to process the next record.
Algorithmic Implementation (C#)
public class SortAlgorithm {
// Insertion sort
public static void InsertSort<T, C>(T[] array, C comparer)
where C:IComparer<T>
{
for (int i = 1; i <= array.Length - 1; i++) {
//Console.Write("{0}: ", i);
int j = i;
while (j>=1 && comparer.Compare(array[j], array[j - 1]) < 0) {
swap(ref array[j], ref array[j-1]);
j--;
}
//Console.WriteLine();
//AlgorithmHelper.PrintArray(array);
}
}
// Ith and j th elements i n exchange array
private static void swap<T>(ref T x,ref T y) {
// Console.Write("{0}<-->{1} ", x, y);
T temp = x;
x = y;
y = temp;
}
}The Console.WriteLine() method and AlgorithmHelper.PrintArray() method above are just for testing convenience, and the PrintArray() method prints the contents of the array in turn. The swap < T >() method is used to swap two records in an array and print the number of swaps (i commented out here, but i can uncomment them in the test). The outer for loop control variable i represents the current processing of Article i records.
public class AlgorithmHelper {
// Print Array Content
public static void PrintArray<T>(T[] array) {
Console.Write(" Array:");
foreach (T item in array) {
Console.Write(" {0}", item);
}
Console.WriteLine();
}
}
// Obtain Comparer and compare
public class ComparerFactory {
public static IComparer<int> GetIntComparer() {
return new IntComparer();
}
public class IntComparer : IComparer<int> {
public int Compare(int x, int y) {
return x.CompareTo(y);
}
}
}In the above code, we created a ComparerFactory class to obtain an IntComparer object, which implements the IComparer < T> interface and specifies the rules for comparing the sizes between two key codes of type int. If you have a custom type, such as MyType, you just need to add another class in ComparerFactory, such as MyTypeComparer, and then let this class implement the IComparer < T > interface, and finally add a method to return to MyTypeComparer.
Output demonstration (C#)
Next, let's look at the client code and output:
static void Main(string[] args) {
int[] array = {42,20,17,13,28,14,23,15};
//int[] array = { 9, 8, 7, 6, 5, 4, 3, 2, 1, 0 };
AlgorithmHelper.PrintArray(array);
SortAlgorithm.InsertSort
(array, ComparerFactory.GetIntComparer());
}
Algorithmic Implementation (C++)
// Sort int types
class IntComparer{
public:
static bool Smaller(int x, int y){
return x<y;
}
static bool Equal(int x, int y){
return x==y;
}
static bool Larger(int x, int y){
return x>y;
}
};
// Insertion sort
template <class T, class C>
void InsertSort(T a[], int length){
for(int i=1;i<=length-1;i++){
int j = i;
while(j>=1 && C::Smaller(a[j], a[j-1])){
swap(a[j], a[j-1]);
j--;
}
}
}2. Bubble Sorting
Algorithmic thought
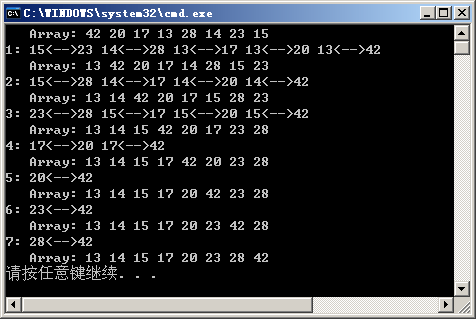
If you have never learned the algorithm knowledge and need to design an array sorting algorithm, it is very likely that the bubble sorting algorithm is designed. Because it's easy to understand and implement. It also contains two loops, assuming that the array length is n, and the outer loop control variable i increases from 0 to n-2. This outer loop does not process a record, but only controls the number of comparisons, from 0 to n-2, a total of n-1 comparisons. Why do n records only need to be compared n-1 times? We can first look at the simplest sorting of two numbers: 4 and 3. If we compare them once, we can get 3 and 4. More records can be analogized.
The exchange of array records is accomplished by inner loop, and the initial value of control variable j is n-1 (array subscript), which decreases to 1. If the previous record is larger than the key code of the current record, the array record is swapped from the end of the array until the subscript of the current record is 1 (at this time the subscript of the previous record is 0). The whole process is like a bubble rising from the bottom, so the sorting algorithm is named bubble sorting.
Let's take a look at it. After the first cycle, the smallest record is located at the top of the array (subscript 0); after the second cycle, the smallest record is located at the second (subscript 1); and after the n-1 cycle, the smallest record is located at the n-1 (subscript n-2) of the array. There is no need to go through the nth loop at this point, because the last one is already at the end of the array (subscripted n-1).
Algorithmic Implementation (C#)
// Bubble sort
public static void BubbleSort<T, C>(T[] array, C comparer)
where C : IComparer<T>
{
int length = array.Length;
for (int i = 0; i <= length - 2; i++) {
//Console.Write("{0}: ", i + 1);
for (int j = length - 1; j >= 1; j--) {
if (comparer.Compare(array[j], array[j - 1]) < 0) {
swap(ref array[j], ref array[j - 1]);
}
}
//Console.WriteLine();
//AlgorithmHelper.PrintArray(array);
}
}Output demonstration (C#)
static void Main(string[] args) {
int[] array = {42,20,17,13,28,14,23,15};
AlgorithmHelper.PrintArray(array);
SortAlgorithm.BubbleSort
(array, ComparerFactory.GetIntComparer());
}
Algorithmic Implementation (C++)
// Bubble sort
template <class T, class C>
void BubbleSort(T a[], int length){
for(int i=0;i<=length-2;i++){
for(int j=length-1; j>=1; j--){
if(C::Smaller(a[j], a[j-1]))
swap(a[j], a[j-1]);
}
}
}3. Selective Sorting
Algorithmic thought
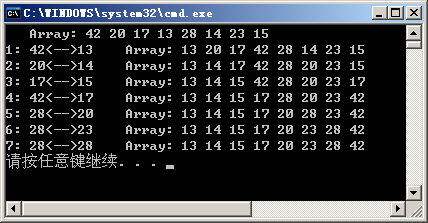
Selective sorting is an improvement on bubble sorting. From the output of the above bubble sorting, it can be seen that in the first pass, in order to mark the minimum value 13 from the first position of the array bubbling at the end of the array to zero, several exchanges were made. For each subsequent trip, a similar exchange will take place.
The idea of sorting is to search the whole array for the first time, find the smallest one, and then place it in the zero position of the array; for the second time, search the n-1 records of the array, find the smallest one (the smallest one for the whole array), and then place it in the first position of the array. In the first pass, search the n-i+1 record of the array, find the smallest record (the smallest for the entire array), and then place it i n the position of the array i-1 (note that the array starts with zero). As can be seen, selection sort significantly reduces the number of swaps.
It should be noted that the inner loop does not need to descend to 1 position on the first trip, as long as the loop is the same as i, because the previous position must be smaller than it (i is smaller). In addition, the inner loop is j > i, not j > = i, because I is saved in lowest index immediately after entering the loop.
Algorithmic Implementation (C#)
public static void SelectionSort<T, C>(T[] array, C comparer)
where C : IComparer<T>
{
int length = array.Length;
for (int i = 0; i <= length - 2; i++) {
Console.Write("{0}: ", i+1);
int lowestIndex = i; // Array Index of Minimum Records
for (int j = length - 1; j > i; j--) {
if (comparer.Compare(array[j], array[lowestIndex]) < 0)
lowestIndex = j;
}
swap(ref array[i], ref array[lowestIndex]);
AlgorithmHelper.PrintArray(array);
}
}Output demonstration (C#)
static void Main(string[] args) {
int[] array = {42,20,17,13,28,14,23,15};
AlgorithmHelper.PrintArray(array);
SortAlgorithm.SelectionSort
(array, ComparerFactory.GetIntComparer());
}
Algorithmic Implementation (C++)
// Selection sort
template <class T, class C>
void SelectionSort(T a[], int length) {
for(int i = 0; i <= length-2; i++){
int lowestIndex = i;
for(int j = length-1; j>i; j--){
if(C::Smaller(a[j], a[lowestIndex]))
lowestIndex = j;
}
swap(a[i], a[lowestIndex]);
}
}4. Hill Sort
Hill sort takes advantage of a feature of insertion sort to optimize the sorting algorithm. This feature of insertion sort is that when the array is basically ordered, the efficiency of insertion sort is relatively high. For example, for an array like this:
int[] array = { 1, 0, 2, 3, 5, 4, 8, 6, 7, 9 };The output of the insertion sort is as follows:
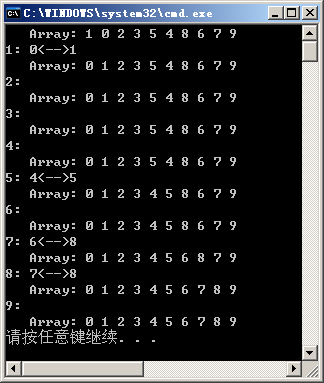
It can be seen that although the number of comparisons has not decreased, the number of exchanges is significantly less. The overall idea of Hill sorting is to make arrays basically ordered before applying insert sorting. The specific process is as follows: suppose there is an array int a []= {42, 20, 17, 13, 28, 14, 23, 15}, without losing generality, we set its length as length.
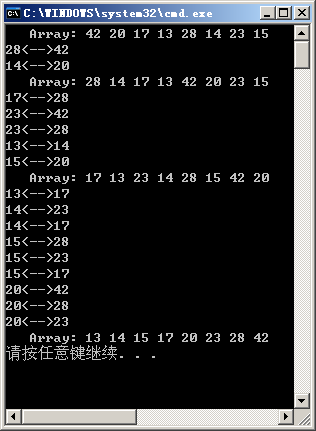
In the first step, step = length/2 = 4, the array is divided into four groups, with two records in each group, and the subscripts are (0,4) (1,5) (2,6) (3,7) respectively; when converted into values, the subscripts are {42,28}, {20,14}, {17,23}, {13,15}. Each group is then sorted by insertion, and then the number of groups is {28,42}, {14,20}, {17,23}, {13,15}, while the actual value of the original array becomes {28,14,17,13,42,20,23,15}. Note here is the position recorded in the original array in the grouping. For the second grouping {14,20}, its subscript is (1,5), so the subscripts of the two records in the original array are a[1]=14;a[5]=20, respectively.
In the second step, step = step/2 = 2, dividing the array into two groups with four records in each group, the subscripts are (0, 2, 4, 6) (1, 3, 5, 7), and converted to values of {28, 17, 42, 23}, {14, 13, 20, 15}, then inserting and sorting each group to get {17, 23, 28, 42} {13, 14, 15}. At this point, the array becomes {17, 13, 23, 14, 28, 15, 42, 20} and is basically ordered.
In the third step, step=step/2 = 1. At this time, a complete insertion sort is performed and the final result {13, 14, 15, 17, 20, 23, 28, 42} is obtained.
Algorithmic Implementation (C#)
// Shell Sort
public static void ShellSort<T, C>(T[] array, C comparer)
where C : IComparer<T>
{
for (int i = array.Length / 2; i >= 1; i = i / 2) {
Console.Write("{0}: ", i);
for (int j = 0; j < i; j++) {
InsertSort(array, j, i, comparer);
}
Console.WriteLine();
AlgorithmHelper.PrintArray(array);
}
}
// Insertion sort for Hill sort
private static void InsertSort<T, C>
(T[] array, int startIndex, int step, C comparer)
where C : IComparer<T>
{
for (int i = startIndex + step; i <= array.Length - 1; i += step) {
int j = i;
while(j>= step && comparer.Compare(array[j], array[j - step]) <0 ){
swap(ref array[j], ref array[j - step]);
j -= step;
}
}
}Notice the insertion of the parameters of the sort InsertSort() method. startIndex is the starting index of the group and step is the step size. It can be seen that the previous insertion sort is only a special case of Step = 1 and startIndex = 0 here.
Output demonstration (C#)
static void Main(string[] args) {
int[] array = {42,20,17,13,28,14,23,15};
AlgorithmHelper.PrintArray(array);
SortAlgorithm.ShellSort
(array, ComparerFactory.GetIntComparer());
}
Algorithmic Implementation (C++)
// Shell Sort
template<class T, class C>
void ShellSort(T a[], int length){
for(int i = length/2; i >= 1; i = i/2 ){
for(int j = 0; j<i; j++){
InsertSort<T, C>(&a[j], length-1, i);
}
}
}
// Insertion sort for Hill sort
template<class T, class C>
void InsertSort(T a[], int length, int step){
for(int i = step; i<length; i+= step){
int j = i;
while(j>=step && C::Smaller(a[j], a[j-step])){
swap(a[j], a[j-step]);
j-=step;
}
}
}For the code of the above three algorithms, insertion sort, bubble sort and selection sort are all(n2), while Hill sort is slightly better, is(n1.5). For algorithm analysis, you can refer to relevant books. Here is a recommendation< Data Structure and Algorithmic Analysis (C++ Version) 2nd Edition "And" Algorithms I~IV (C++ Implementation) - Basis, Data Structure, Sorting and Searching It's very good. I mainly refer to these two books.