Data Structure and Algorithms-String Sorting
For many sorting applications, the keys that determine the order are strings. Next, you'll learn about string-specific sorting methods that are more efficient than the general sorting methods you learned earlier, such as bubbles, inserts, merges, and so on.
The first method is the low-bit-first (LSD) string sorting method. This algorithm requires that each string in the sorting be equal in length. It treats the string as a number and checks the character from the right side of the string to the left (equivalent to from the lowest to the highest position of the number).
The second method is high-bit-first (MSD) string sorting. It does not require an ordered string to be equal in length, and it does not necessarily require checking all inputs to complete the ordering. The algorithm will check the characters from left to right (as we usually compare strings) and sort the strings in a similar way to fast sort.
When learning low-bit-first string sorting, it's better to know the count sorting and cardinal sorting first. The last article has been described in detail, and I will not repeat it here.
Low-bit-first string sorting LSD
Firstly, the length of the strings to be sorted is the same, set to W. Each character is used as the keyword from right to left, and the strings are sorted W times by counting sort method. Because the counting sorting method is stable, the low-bit-first string sorting can stably sort the strings.
Suppose you have some knowledge of counting sort and cardinality sort, the code is given directly here.
package Chap5; import java.util.Arrays; public class LSD { public static void sort(String[] a, int W) { // Each digit ranges from 0 to 9, with a base of 10. int R = 256; int N = a.length; String[] aux = new String[N]; int[] count = new int[R+1]; // A total of d-round count sorting is required, starting from the last bit, in the right-to-left order. for (int d = W - 1; d >= 0; d--) { // 1. Calculate the frequency by adding an additional 1 to the required array length for (int i = 0; i < N; i++) { // With the index after adding 1, the location increases with repetition. count[a[i].charAt(d) + 1]++; } // 2. Beginning Index of Frequency - > Element for (int r = 0; r < R; r++) { count[r + 1] += count[r]; } // 3. Elements are classified according to the initial index, using a temporary array as large as the array to be arranged to store data. for (int i = 0; i < N; i++) { // After filling in one data, self-increment is made so that the same data can be filled into the next vacancy. aux[count[a[i].charAt(d)]++] = a[i]; } // 4. Data Writing Back for (int i = 0; i < N; i++) { a[i] = aux[i]; } // Reset count [], for the next round of Statistics for (int i = 0; i < count.length; i++) { count[i] = 0; } } } public static void main(String[] args) { String[] a = {"4PGC938", "2IYE230", "3CIO720", "1ICK750", "1OHV845", "4JZY524", "1ICK750", "3CIO720", "1OHV845", "1OHV845","2RLA629", "2RLA629", "3ATW723"}; LSD.sort(a, 7); System.out.println(Arrays.toString(a)); } }
The above program will print the following
[1ICK750, 1ICK750, 1OHV845, 1OHV845, 1OHV845, 2IYE230, 2RLA629, 2RLA629, 3ATW723, 3CIO720, 3CIO720, 4JZY524, 4PGC938]
Let's look at the LSD trajectory of sorting these strings.
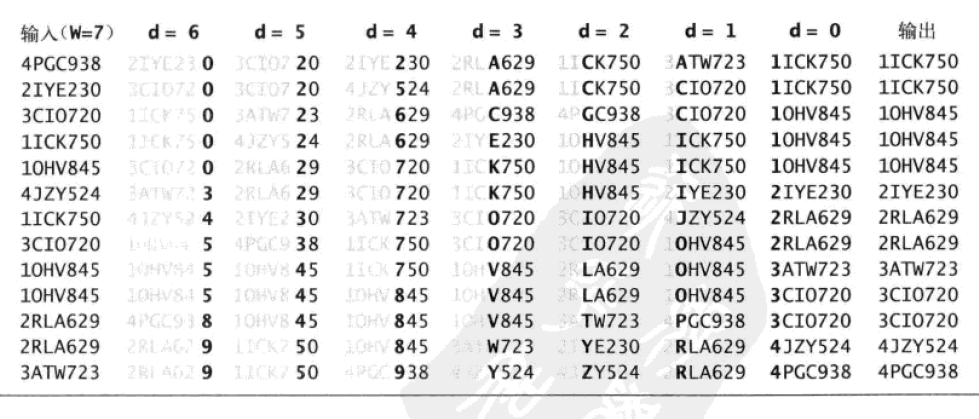
Why is it possible to sort strings W times from right to left with each character as the key? Imagine a simple case: if there are two keys whose zeroth position is not sorted and they are the same, then the difference in the string is the first position that has been sorted, and they will remain ordered for the sake of the stability of the counting sort; unless the first character that is not sorted is different, then the sorted character is meaningless for the final order of the two. Later, a round of processing will modify the order of the keys according to the different higher characters. For example, ["SC", "SB", "AD"], after sorting with the first character as the key, is ["SB", "SC", "AD"] for "SB" and "SC" their 0th position has not been sorted and the same, because the counting order is stable, in this case, they will be sorted with the 0th position, and for "SB" and "AD" their 0th position has not been sorted and different, then the results of the 1st order will be meaningless, because of the stability of the counting order. In order to sort the 0th bit into ["AD", "SB", "SC"], you can see that the first bit of the original string is the order of BD, and then the order of DB. To sum up: Our goal is to keep the lower order under the same higher-bit characters; in the case of different higher-bit characters, it is no longer meaningful to ensure that the higher-bit characters are orderly and the lower-bit order is meaningless.
Standard LSD can only handle equal-length strings. The following is a general string sorting method (string length is not necessarily the same). First, let's look at the high-bit-first string sorting MSD.
High-bit-first string sorting MSD
High-bit-first string sorting MSD can handle unequal-length strings. It checks each character from left to right, counts the frequency of the first letter of the string, and classifies and sorts the first letter according to it. Then, it classifies all the first letters into a subarray, and sorts these subarrays recursively. The refinement point is:
- Sort the arrays by first letters and divide them into sub-arrays with the same first letters
- Ignore all the same initials and sort subarrays recursively

In the high-bit-first string sorting algorithm, special attention should be paid to the situation at the end of the string. We need a tag to determine whether we reach the end of the string, so we need to define a position at the end of the string in the character set, and the end of the string should be smaller than any character, such as "other" is smaller than "others", so the integer corresponding to the end of the string in the character set should be the smallest. So we can rewrite String's charAt method and return - 1 when the index reaches the end of the string. But our count [] array index can't be negative, so we add 1 to each index returned. That is, 1 represents the first character, 2 represents the second character, 0 represents the end of the string. The charAt method is as follows
private static int charAt(String s, int d) { if (d < s.length()) { return s.charAt(d); } else { return -1; } }
We will see that in the following program, where all the charAt methods are invoked, we will a d d 1, like charAt(a[i], d) + 1.
Since the end of the string occupies a position in the character set, the count [] array should also have an additional position, and the length of the array should be changed from R+1 to R+2.
With these preparatory foundations, it is not difficult to implement MSD.
package Chap9; import java.util.Arrays; public class MSD { // base private static int R = 256; // Threshold for switching to insertion sort private static int M = 15; public static void sort(String[] a) { int N = a.length; String[] aux = new String[N]; sort(a, aux, 0, a.length - 1, 0); } private static void sort(String[] a, String[] aux, int low, int high, int d) { // For small arrays, switch to insert sort if (high <= low + M) { insertSort(a, low, high, d); return; } // Adding 1 to the original R+1 is because to store the end of the string in count[1], count[0] is still zero. int[] count = new int[R + 2]; // Statistical frequency for (int i = low; i <= high; i++) { count[charAt(a[i], d) + 2]++; } // Convert to start index for (int r = 0; r < R + 1; r++) { count[r+1] += count[r]; } // data classification for (int i = low; i <= high; i++) { aux[count[charAt(a[i], d) + 1]++] = a[i]; } // Write back to the original array for (int i = low; i <= high ; i++) { a[i] = aux[i-low]; } // Recursive sorting with each character as the key // In fact, every recursive process is a subarray with the same initial. // [low + count[r], low + count[r+ 1] -1] are subarray intervals with the same initials // d+1 denotes ignoring the same initials and counting frequency - > counting sort from the next character for (int r = 0; r < R; r++) { sort(a, aux, low + count[r], low + count[r+ 1] -1, d + 1); } } private static int charAt(String s, int d) { if (d < s.length()) { return s.charAt(d); } else { return -1; } } private static void insertSort(String[] a, int low, int high, int d) { for (int i = low + 1; i <= high; i++) { // If the current index is larger than its previous element, no insertion is required; otherwise, insertion is required. if (less(a[i], a[i - 1], d)) { // Save the elements to be inserted first String temp = a[i]; // Right shift of elements int j; for (j = i; j > low && less(temp, a[j - 1], d); j--) { a[j] = a[j - 1]; } // insert a[j] = temp; } } } private static boolean less(String v, String w, int d) { return v.substring(d).compareTo(w.substring(d)) < 0; } public static void main(String[] args) { String[] a = {"she", "sells", "seashells", "by", "the", "sea", "shore", "the", "shells", "she", "sells", "are", "surely", "seashells"}; MSD.sort(a); System.out.println(Arrays.toString(a)); /* Output: [are, by, sea, seashells, seashells, sells, sells, she, she, shells, shore, surely, the, the] */ } }
As you can see, the core sort method only adds the last for loop on the basis of the sorting of numbers. Looking at the parameter list, the interval count[r]~count[r+1] - 1 represents all the characters indexed as R (they are all the same), and low is added at both ends of the interval to indicate the beginning index and the end index (closed interval) of the characters indexed as R. Then d + 1 is because when sorting subarrays, because the initial letters are the same, it ignores the statistics of frequency, sorting and so on for the next character.
The following sorting procedure (assuming M=0, without switching the sorting method) can help you better understand the algorithm. You can see that the initial letters between low and high are the same, and the black character is the character whose d+1 bit is being sorted.

In the above implementation, there is an insertion sort for strings. When the length of the partitioned array is very small (for example, only a dozen elements), it will switch to the insertion sort to sort the strings directly. At the same time, in order to avoid repeated checking of known identical characters, the less method is also rewritten. For strings with the same characters in the first d, the comparison will begin directly from the index D.
Special handling of small arrays is necessary. As with quick sorting, this method of recursively cutting molecular arrays generates a large number of micro arrays. For each subarray, you need to create a count of 258 elements [] and convert the frequency to an index. This cost is much higher than other sorting methods, and if you use a 16-bit Unicode character set (R=65535), the sorting process may slow down thousands of times. Therefore, switching decimal arrays to insert sort is necessary for high-bit-first string sort.
MSD sorts subarrays with a large number of equivalent keys very slowly, and if there are too many identical strings, the switching sorting method will not be invoked. The worst case is that all strings to be sorted are equal, while low and high keep their original values (low=0, hgih=a.length - 1), and do not switch to insertion sort, and for the same string, recursive sort checks all characters.
MSD is based on counting sorting and uses insertion sorting when switching sorting methods, so the high-bit-first string sorting is stable in general.
Quick Sorting of Three-Directional Strings
Remember Quick Sorting of Three Directional Segmentation Do you? We can use its idea to divide the string array into three sub-arrays: a sub-array containing all the initials less than the segmentation character, a sub-array containing all the initials equal to the segmentation character, and a sub-array containing all the initials greater than the segmentation character. Then sort these three arrays recursively. Note that for all subarrays whose initial letters are equal to the segmentation characters, the initial letters should be ignored in the recursive sorting (as in MSD).

Comparing with the fast sorting code of three-way segmentation, the quick sorting of three-way strings can be realized with a little modification.
package Chap5; import java.util.Arrays; public class Quick3String { // Threshold for switching to insertion sort private static int M = 15; public static void sort(String[] a) { sort(a, 0, a.length - 1, 0); } private static void sort(String[] a, int low, int high, int d) { if (high <= low + M) { insertSort(a, low, high, d); return; } int lt = low; int gt = high; int i = low + 1; // The syncopated character v is the d-th character of a[low] int v = charAt(a[low], d); while (i <= gt) { int t = charAt(a[i], d); if (t < v) { swap(a, lt++, i++); } else if (t > v) { swap(a, i, gt--); } else { i++; } } // Now a [lo. lt-1] < v = a [lt. gt] < a [gt + 1. high] is established // Arrays with the same segmentation elements will not be accessed by recursive algorithms, and the subarrays around them will be sorted recursively. sort(a, low, lt - 1, d); // All sub-arrays with the same initials as the synthesized characters, recursive sorting, and the same initials to be ignored as in MSD if (v >= 0) { sort(a, lt, gt, d+ 1); } sort(a, gt + 1, high, d); } private static void swap(String[] a, int p, int q) { String temp = a[p]; a[p] = a[q]; a[q] = temp; } private static int charAt(String s, int d) { if (d < s.length()) { return s.charAt(d); } else { return -1; } } private static void insertSort(String[] a, int low, int high, int d) { for (int i = low + 1; i <= high; i++) { // If the current index is larger than its previous element, no insertion is required; otherwise, insertion is required. if (less(a[i], a[i - 1], d)) { // Save the elements to be inserted first String temp = a[i]; // Right shift of elements int j; for (j = i; j > low && less(temp, a[j - 1], d); j--) { a[j] = a[j - 1]; } // insert a[j] = temp; } } } private static boolean less(String v, String w, int d) { return v.substring(d).compareTo(w.substring(d)) < 0; } public static void main(String[] args) { String[] a = {"she", "sells", "seashells", "by", "the", "sea", "shore", "the", "shells", "she", "sells", "are", "surely", "seashells"}; Quick3String.sort(a); System.out.println(Arrays.toString(a)); } }
The recursive call trajectory of three-way string sorting is shown in the following figure.
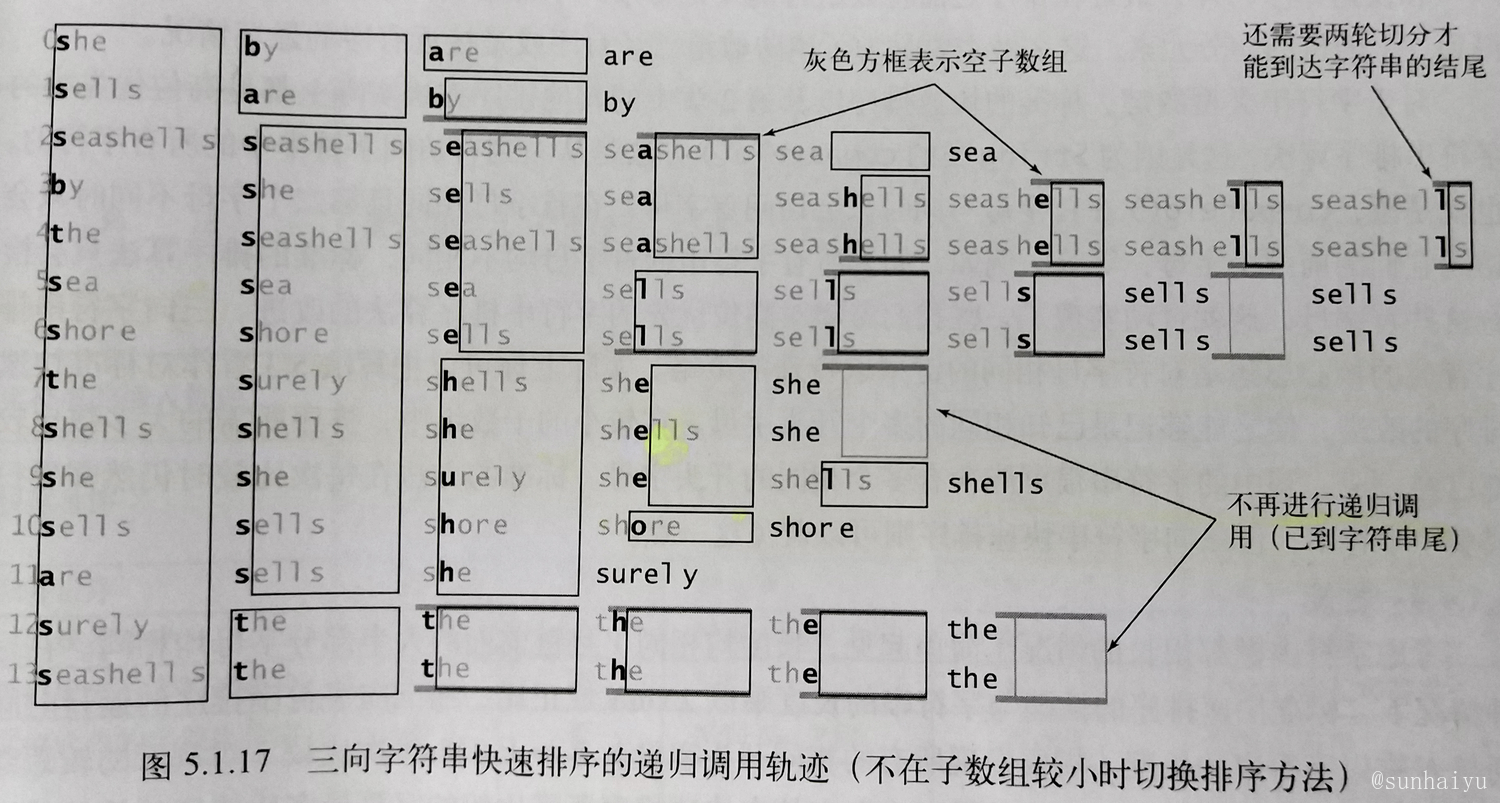
Like MSD, insertion sort is switched to handle decimal arrays, although it is far less important in fast sorting of three-way sliced strings than in MSD. Quick sorting of three-way segmentation uses the first element of the subarray as the segmentation point, and fast sorting of three-way segmentation strings uses the d-th character of the first string of the subarray as the segmentation character. Then in the recursive sorting of subarrays, compared with the fast sorting of three-way segmentation, the fast sorting of three-way segmentation strings has such a judgment. This sentence means that as long as the end of the string has not arrived (v = 1 means arrival, the rest has not arrived), all subarrays with the same initials and segmentation characters also need to be sorted recursively, but to ignore the same as MSD. First letter, process the next character.
if (v >= 0) { sort(a, lt, gt, d+ 1); }
MSD may create a large number of (empty) subarrays, whereas three-way string sorting only divides the array into three parts. Therefore, three-way string sorting can deal with equivalence keys, keys with long common prefixes, keys and small arrays with a smaller range of values. And three-way string quick sorting does not require additional space, MSD needs count [] and aux [], which are better than MSD.
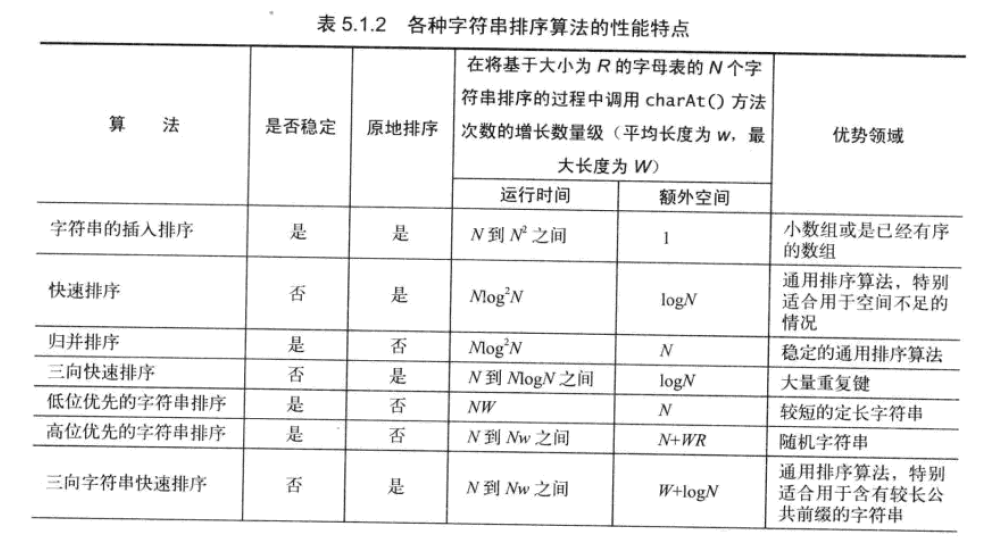
The following table summarizes the performance characteristics of various string sorting algorithms.
by @sunhaiyu
2017.11.22