Stack

In some places called stacks, stacks are containers that can store data elements, access elements, and delete elements. The feature of stacks is that they allow operations that add data (English: push) and output data (English: pop) only at one end of the container (called top indicator of stack).Without the concept of location, the element that can be accessed or deleted at any time is the last one saved before, and a default access order is determined.
Operate according to the principle of LIFO (Last In First Out)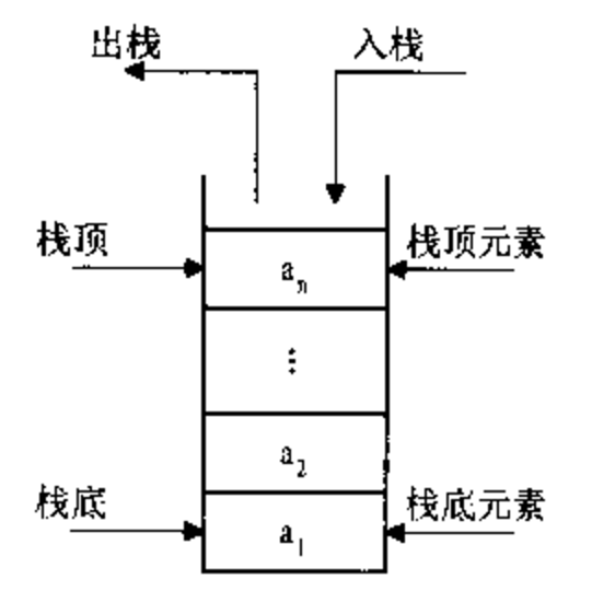

Implementation and operation of stack structure

Stack can be implemented with: Sequential Table, Chain Table

class Stack(object):
    """Stack"""
    def __init__(self):
         self.items = []

    def is_empty(self):
        """Determine whether it is empty"""
        return self.items == []

    def push(self, item):
        """Add elements"""
        self.items.append(item)

    def pop(self):
        """Pop-up Element"""
        return self.items.pop()

    def peek(self):
        """Return to top of stack element"""
        return self.items[len(self.items)-1]

    def size(self):
        """Return stack size"""
        return len(self.items)

queue

A queue is a linear table that allows insert operations only at one end and delete operations at the other end.A queue is a linear First In First Out (FIFO).

Queue operation

class Queue(object):
    """queue"""
    def __init__(self):
        self.items = []

    def is_empty(self):
        return self.items == []

    def enqueue(self, item):
        """Queue"""
        self.items.insert(0,item)

    def dequeue(self):
        """Out of Queue"""
        return self.items.pop()

    def size(self):
        """Return size"""
        return len(self.items)

Double-ended Queue

A double-ended queue is a data structure with the properties of queues and stacks.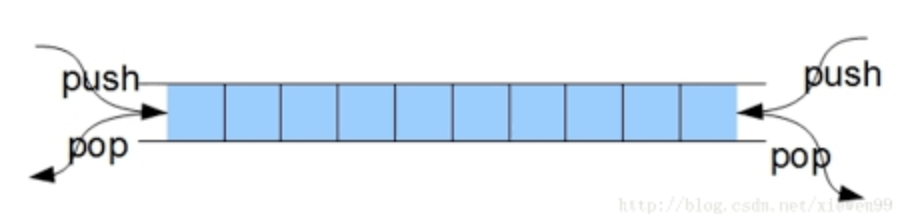

class Deque(object):
    """Double-ended Queue"""
    def __init__(self):
        self.items = []

    def is_empty(self):
        """Determine if the queue is empty"""
        return self.items == []

    def add_front(self, item):
        """Add elements to the queue head"""
        self.items.insert(0,item)

    def add_rear(self, item):
        """Add elements at the end of the queue"""
        self.items.append(item)

    def remove_front(self):
        """Remove element from queue head"""
        return self.items.pop(0)

    def remove_rear(self):
        """Remove element from end of queue"""
        return self.items.pop()

    def size(self):
        """Return Queue Size"""
        return len(self.items)

Sorting and Searching

Stability of sorting algorithm

Stability: The stable sorting algorithm maintains relative order for records that originally have the same key values.That is, if a sorting algorithm is stable, when there are two records of R and S with equal key values and R appears before S in the original list, R will also be before S in the sorted list.

Bubble sort

Bubble Sort:

1. Compare adjacent elements.If the first is larger than the second (ascending), swap the two.
2. Do the same work for each pair of adjacent elements, from the first pair at the beginning to the last pair at the end.When this is done, the last element will be the maximum number.
3. Repeat the above steps for all elements except the last one.
4. Continue repeating the above steps for fewer and fewer elements each time until no pair of numbers need to be compared.

def bubble_sort(alist):
    for j in range(len(alist)-1,0,-1):
        # j means that the number of comparisons needed for each traversal is decreasing
        for i in range(j):
            if alist[i] > alist[i+1]:
                alist[i], alist[i+1] = alist[i+1], alist[i]

li = [54,26,93,17,77,31,44,55,20]
bubble_sort(li)
print(li)

Select Sort

Selection sort:

1. Start with the first element, and then compare with the following elements. If you encounter a smaller element than the first one, the selection state is modified to a smaller one. After traversing, select the smallest element and place it in the first one.
2. Just follow this principle, traverse n-1 times.

def selection_sort(alist):
    n = len(alist)
    # n-1 selection is required
    for i in range(n-1):
        # Record Minimum Position
        min_index = i
        # Select the minimum data from the i+1 position to the end
        for j in range(i+1, n):
            if alist[j] < alist[min_index]:
                min_index = j
        # If the selected data is not in the correct location, exchange it
        if min_index != i:
            alist[i], alist[min_index] = alist[min_index], alist[i]

alist = [54,226,93,17,77,31,44,55,20]
selection_sort(alist)
print(alist)

Insert Sort

Insert Sort (English: Insertion Sort):

1. Compare the sizes based on the two elements at the start, excluding the order
2. Select elements from an unordered list and insert them into the preceding ordered list in turn

def insert_sort(alist):
    # Insert forward from the second position, which is the element subscripted to 1
    for i in range(1, len(alist)):
        # Compare forward from the first element, swap positions if less than the previous element
        for j in range(i, 0, -1):
            if alist[j] < alist[j-1]:
                alist[j], alist[j-1] = alist[j-1], alist[j]

alist = [54,26,93,17,77,31,44,55,20]
insert_sort(alist)
print(alist)