Catalog
1.2 Three-step analysis of quick sorting using divide-and-conquer strategy
1.3 Comparison of Merge Sorting and Quick Sorting
3.1 Implementation Mode 1: Select the intermediate value as the benchmark value
3.2 Implementation Mode 2: Select the rightmost value as the benchmark value
1. Basic Ideas
1.1 Basic Thought
- Quick sorting is a sort based on divide-and-conquer strategy
-
basic thought
- 1. Benchmark: First, take a number from the sequence as the benchmark.
- 2. Partitioning process: Put all the numbers larger than this number on its right, and all the numbers smaller than or equal to it on its left.
- 3. Repeat the first and second steps to the left and right intervals until there is only one number in each interval.
- Note: Quick sorting is done when sorting.
1.2 Three-step analysis of quick sorting using divide-and-conquer strategy
- 1. Decomposition: The array A [p. r] is divided into two (possibly empty) subarrays A[p...q-1] and A[q+1...r], so that each element in A[p...q-1] is less than or equal to A[q], and A[q] is less than or equal to each element in A[q+1...r].
- 2. Solution: Sort subarrays A[p...q-1] and A[q+1...r] by fast sorting through recursive calls
- 3. Merge: Because subarrays are sorted in the original address, no merge operation is required: Array A[p...r] is already ordered
1.3 Comparison of Merge Sorting and Quick Sorting
- Merge sort divides arrays into several sub-arrays and sorts them separately, and merges the ordered sub-arrays into the whole array; while fast sort is when both sub-arrays are ordered, the whole array will be ordered naturally.
- Merge sorting does not do any processing in sorting, while quick sorting does element exchange in sorting, keeping the left element less than the reference value and the right element larger than the reference value.
- The merge sort recursive call occurs before the entire array is processed, and the quick sort recursive call occurs after the entire array is processed.
- Merge sorting completes sorting at merge time, quick sorting completes sorting at split time, and doing nothing at merge time
- In merge sorting, an array is divided into two halves. In fast sorting, the location of the segmentation depends on the content of the array.
2. Graphical Principle
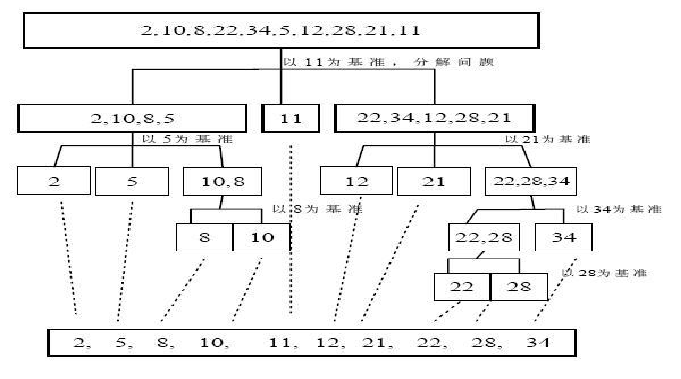
3. Code Implementation
Keyword Interpretation
- pivot: Base element
- Partition: partition the entire array
3.1 Implementation Mode 1: Select the intermediate value as the benchmark value
public class QuickSort extends Sort {
/**
* sort Method provides a unified call "interface" for the outside world
* @param arr
*/
@Override
public void sort(Comparable[] arr) {
quickSort(arr,0,arr.length-1);
}
private void quickSort(Comparable[] arr,int left,int right){
if(left >= right){
return;
}
//Final index of benchmark value after segmentation
int pivot = partition(arr,left,right);
//Recursive segmentation on the left side of pivot
quickSort(arr,left,pivot-1);
//Recursive segmentation of the right side of pivot
quickSort(arr,pivot+1,right);
}
/**
* The cut group is divided into left less than pivot and right more than pivot.
* @param arr
* @param left
* @param right
* @return Returns the index value of the intermediate benchmark pivot
*/
private int partition(Comparable[] arr,int left,int right){
//Let's take the median benchmark here.
Comparable pivot = arr[(left+right)/2];
//Define two pointers pointing to both sides
int move_right = left;
int move_left = right;
/**
* When the two pointers are equal or move to the right more than the pointer move to the left, they represent traversal of all elements.
*
* while The purpose of the loop is to have elements smaller than pivot on the left and elements larger than pivot on the right.
*/
while(move_right < move_left){
/**
* Move the pointer to the right to find a value greater than or equal to pivot.
*
*
* The final case is that the left side of pivot is all smaller than pivot, and then the pivot value is found.
* Then if the non-pivot is found on the right, the exchange takes place. If it is equal to pivot, move_right is not necessarily equal to move_left.
*
* Since there may be multiple duplicate values that are the same as pivot itself, after swapping, we also need to keep the pointer moving.
* Make sure that the loop ends by judging the relative size of the pointer. Otherwise, if the pointer is not moved after the exchange, it may form a dead loop (two pointers point to two adjacent pivot s at the same time).
*
*/
while(arr[move_right].compareTo(pivot) < 0){
//The pointer pointing to the right is less than the pivot value. Without swapping, the pointer continues to move to the right.
move_right++;
}
/**
* Move the pointer left to find values less than or equal to pivot
*
* Ibid., the last thing is to find pivot.
*/
while (arr[move_left].compareTo(pivot) > 0){
//The left-shift pointer points to a value larger than pivot. Without swapping, the pointer continues to move left.
move_left--;
}
//Two pointers traverse all elements, ending the loop
if(move_right >= move_left)
break;
//Exchange values pointed by two pointers
swap(arr,move_right,move_left);
/**
* Iterate to move the pointer
*
* When the pointer points to pivot, let the other pointer close to itself to end the loop.
*/
//If the right pointer points to pivot, the left pointer--
if(arr[move_right].compareTo(pivot) == 0){
move_left--;
}
//If the left-shift pointer points to pivot, the right-shift pointer--
if(arr[move_left].compareTo(pivot) == 0){
move_right++;
}
}
/**
* Ultimately, we need to return the final index of the baseline value used for segmentation.
*
* After the loop, one of the two pointers always points to pivot, and finally returns the index of pivot by following judgment
*/
int pivotIndex;
if(arr[move_right] == pivot){
pivotIndex = move_right;
}else{
pivotIndex = move_left;
}
return pivotIndex;
}
}
import java.util.Arrays;
public class SortTest {
public static void main(String[] args) {
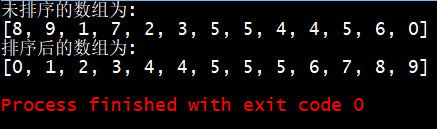
Integer[] arr = new Integer[]{8,9,1,7,2,3,5,5,4,4,5,6,0};
System.out.println("Unordered arrays are:");
System.out.println(Arrays.toString(arr));
QuickSort quickSort = new QuickSort();
quickSort.sort(arr);
System.out.println("The sorted array is:");
System.out.println(Arrays.toString(arr));
}
}
3.2 Implementation Mode 2: Select the rightmost value as the benchmark value
public class QuickSort extends Sort {
/**
* sort Method provides a unified call "interface" for the outside world
*
* @param arr
*/
@Override
public void sort(Comparable[] arr) {
quickSort(arr, 0, arr.length - 1);
}
private void quickSort(Comparable[] arr, int left, int right) {
if (left >= right) {
return;
}
//Final index of benchmark value after segmentation
int pivot = partition(arr, left, right);
//Recursive segmentation on the left side of pivot
quickSort(arr, left, pivot - 1);
//Recursive segmentation of the right side of pivot
quickSort(arr, pivot + 1, right);
}
/**
* The cut group is divided into left less than pivot and right more than pivot.
*
* @param arr
* @param left
* @param right
* @return Returns the index value of the intermediate benchmark pivot
*/
private int partition(Comparable[] arr, int left, int right) {
//Let's take the last value as the benchmark.
Comparable pivot = arr[right];
//Define a pointer, move the record to the right, i point to the next location of the last value less than or equal to pivot
int i = left; //Initialize to start position
//Traversing the elements from left to right-1
for (int j = left; j <= right - 1; j++) {
if (arr[j].compareTo(pivot) <= 0) {
//The current traversal element is less than or equal to the base value
//Exchange the value of the next position (regardless of its size) less than or equal to the last value of pivot with the current traversal element
swap(arr, i, j);
//At this point, the last value less than or equal to pivot is the value after exchange, so the expression before i is less than or equal to pivot.
i++;
}
}
//After this traversal, the values less than or equal to pivot are swapped in front of the i position, and finally the i position itself points to those larger than pivot.
//At this point, the value at the position of i and pivot are exchanged, and finally the left side of pivot is less than or equal to its value, and the right side of pivot is greater than its value.
swap(arr, i, right);
//Finally returns the pivot's final index value, i
return i;
}
}
import java.util.Arrays;
public class SortTest {
public static void main(String[] args) {
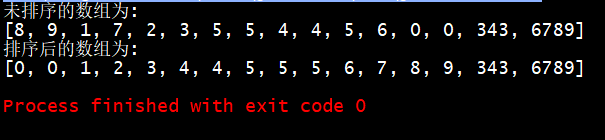
Integer[] arr = new Integer[]{8,9,1,7,2,3,5,5,4,4,5,6,0,0,343,6789};
System.out.println("Unordered arrays are:");
System.out.println(Arrays.toString(arr));
QuickSort quickSort = new QuickSort();
quickSort.sort(arr);
System.out.println("The sorted array is:");
System.out.println(Arrays.toString(arr));
}
}
4. Performance Analysis
- Quick sorting is a sorting algorithm with the worst time complexity of O(n^2).
- But quick sorting is usually the best choice in practical sorting applications, because its average performance is very good - it expects the time complexity to be O(nlgn), and the constant factor implied in O(nlgn) is very small.
- Quick sorting is in-situ sorting, so the spatial complexity is O(1)
- Quick sorting works well in a virtual environment
Code demonstration example:
public class SortPerformanceTest {
public static void main(String[] args) {
//Create 100,000 random data
Double[] arr1 = new Double[100000];
for (int i = 0; i < arr1.length; i++) {
arr1[i] = (Double) (Math.random() * 10000000); //10,000,000 is used here to make the data more dispersed.
}
//Create objects for sorting classes
QuickSort quickSort = new QuickSort();
//Sort arr1 using Hill sort
long quickSort_start = System.currentTimeMillis();
quickSort.sort(arr1);
long quickSort_end = System.currentTimeMillis();
System.out.println("Quick sort takes time:"+(quickSort_end - quickSort_start)+"ms");
}
}

