Stacks and queues are linear tables that restrict the insertion and deletion of total equity changes at the end of the table
Stack -- last in first out
Stack algorithms must be used: number system matching, expression evaluation, bracket matching detection, eight queens problem, line editing program, function call, maze solution and recursive call
Insertion and deletion can only be performed at the end of the table.
Sequential stack
Set the top pointer to point to the top element of the stack and the base pointer to point to the bottom of the stack; However, for ease of operation, top generally points to the subscript address above the top element of the stack, and stacksize indicates the maximum capacity of the stack
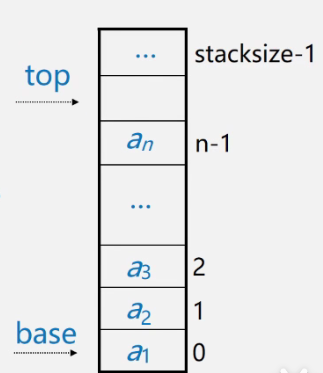
Empty stack: base==top
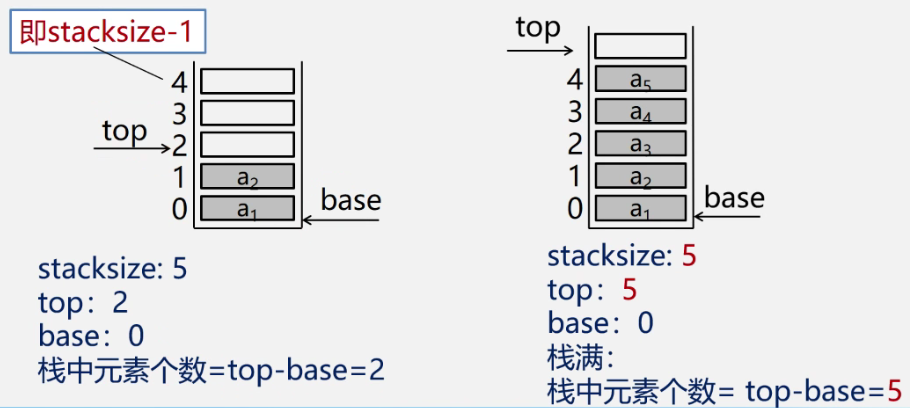
Stack full: top base = stacksize
Overflow: when the stack is full, you have to push in elements Underflow: when the stack is empty, pop up elements
Overflow is generally regarded as an error and underflow as an end condition
realization:
definition
#define MAXSIZE 100
typedef struct{
SElemType *base;//Stack top pointer
SElemType *top;//Stack bottom pointer
int stacksize;//Maximum capacity
}SqStack;Check stack full?
Status StackEmpty(SqStack S){
if(S.top == S.base)
return TURE;
else
return FASLSE;
}initialization
Status InitStack(SqStack &S)
{
S.base= new SElemtype[MAXSIZE];
if(!S.base) exit(OVERFLOW);//Storage allocation failed
S.top=S.base;//Stack empty
S.stacksize = MAXSIZE;
return OK;
}Seeking length
int StackLength(SqStack S)
{
return S.top-S.base;
}Empty stack
Status ClearStack(SqStack S){
if(S.base) S.top = S.base;
return OK;
}Destroy stack
Staus DestroyStack(SqStack &S){
if(S.base){
delete S.base;
S.stacksize=0;
S.base = S.top =NULL;
}
return OK;
}Push
Status Push(SqStack &S,SElemType e){
if(S.top - S.base == S.stacksize)//Stack full
return ERROR;
*S.top++=e; //Or * s.top = E; s.top++;
return OK;
}Out of stack
Status Pop(SqStack &S,SElemType &e){
if(S.top == S.base)//Empty stack detection
return ERROR
e = *--S.top; //--S.top; e=*S.top;
return OK;
}Chain stack
definition
typedef struck StackNode{
SElemType data;
struct StackNode *next;
}StackNode,*LinkStack;
LinkStack S;Head inserting method is convenient for stack operation

The head pointer of the linked list is the top of the stack; No header node is required; The stack is basically not full; An empty stack is equivalent to a header pointer pointing to null; Inserts and deletions are performed only at the top of the stack
initialization
void InitStack(LinkStack &S){
S=NULL;
return OK;
}Air judgment
Status StackEmpty(LinkStack S)
{
if(S==NULL) return TRUE;
else return FALSE;
}Push
Status Push(LinkStack &S,SElemType e){
p = new StackNode;//Generate node p
p->data = e;
p->next = S;
S=p;//Modify stack top pointer
return OK;
}Out of stack
Status Pop(LinkStack &S,SElemType &e){
if(S == NULL) return ERROR;
e = S->data;
p=S;
S=S->next;
delete p;
return OK;
}Get stack top element
SElemType GetTop(LinkStack S){
if(S!=NULL)
return S->data;
}Stack and recursion
definition:
If an object part contains itself or defines itself by itself, the object is called recursive (linked list)
If a procedure calls itself directly or indirectly, it is called a recursive procedure (factorial of n)
Classical recursive problems: mathematical functions defined recursively, data structures with recursive characteristics, and problems that can be solved recursively
General form of divide and conquer method
void p(Parameter table){
if(Recursive end condition) Direct solving steps;--Basic item
else p(Smaller parameters); --Inductive term
}
Ex:
long Fact(long n){
if(n==0) return 1;//Basic item
else return n*Fact(n-1);//Inductive term
}Queue -- first in first out
Sequential queue
definition
#define MAXQSIZE 100
typedef Sturct{
SElemType *base;//Initialized dynamically allocated storage space
int front;//Head pointer
int rear;//Tail pointer
}SqQueue;Solve false overflow (there is still memory space, but Q.rear points to the end of the queue)
1. Move the elements in the team forward in turn Disadvantages: waste of time (all elements need to be moved)
2. When rear = maxqsize, let it point to the head space. The same is true when front is maxqsize

Calculation method: modular operation Insert Q.base[Q.rear] = x;
Q.rear=(Q.rear+1)%MAXQSIZE;
Delete x=Q.base[s.front];
Q.front=(Q.front+1)%MAXQSIZE
Loop queue to judge whether the queue is empty or full (front==rear)
1. Set an additional representation to judge 2. Use one less variable 3. Set another element to record the number
Calculation method of 2 (rear+1)%MAXQSIZE== front
Queue initialization
Status InitQueue(SqQueue &Q){
Q.base = new QElemType[MAXQSIZE]; //Allocate array space
if(!Q.base) exit(OVERFLOW);
Q.front = Q.rear=0;
return OK;
}Find queue length
int QueueLength(SqQueue Q){
return(Q.rear-Q.front+MAXQSIZE)%MAXQSIZE;
}Join the team
Status EnQueue(SqQueue &Q,QElemType e){
if((Q.rear+1)%MAXQSIZE == Q.front) return ERROR;//Team full
Q.base[Q.rear] = e; //New elements join the team
Q.rear = (Q.rear+1)%MAXQSIZE; //Tail pointer + 1
retturn OK;
}Out of the team
Status DeQueue(SqQueue &Q,QElemType &e){
if(Q.front == Q.rear) return ERROR;
e=Q.base[Q.front]; //Save team header element
Q.front=(Q.front+1)%MAXQSIZE;//Counter pointer + 1
return OK;
}Chain queue
definition
#define MAXQSIZE 100
typedef struct Qnode{
QElemType data;
struct Qnode *next;
}QNode,*QueuePtr;initialization
Status InitQueue(LinkQueue &Q){
Q.front==Q.rear = new QNode();
if(!Q.front) exit(OVERFLOW);
Q.front->next=NULL;
return OK;
}Destroy
Status DestroyQueue(LinkQueue &Q){
while(Q.front){
p=Q.front->next; delete Q.front; Q.front=p;
//Q.rear = Q.front->next; delete Q.front; Q.front=Q.rear;
}
return OK;
}Join the team
Status EnQueue(LinkQueue &Q,QElemType e){
p= new QNode();
if(!p) exit(OVERFLOW);
p->data=e; p->next=NULL;
Q.rear->next=p;
Q.rear=p;
return OK;
}Out of the team
Status DeQueue(LinkQueue &Q,QElemType &e){
if(Q.front == Q.rear) return ERROR;
p=Q.front->next;
e=p->data;
Q.front->next=p->next;
if(Q.rear==p) Q.rear=Q.front;
delete p;
return OK;
}