Joint search set

1. Union search set concept

The parallel query set is a tree type data structure. The parallel query set can efficiently perform the following operations:

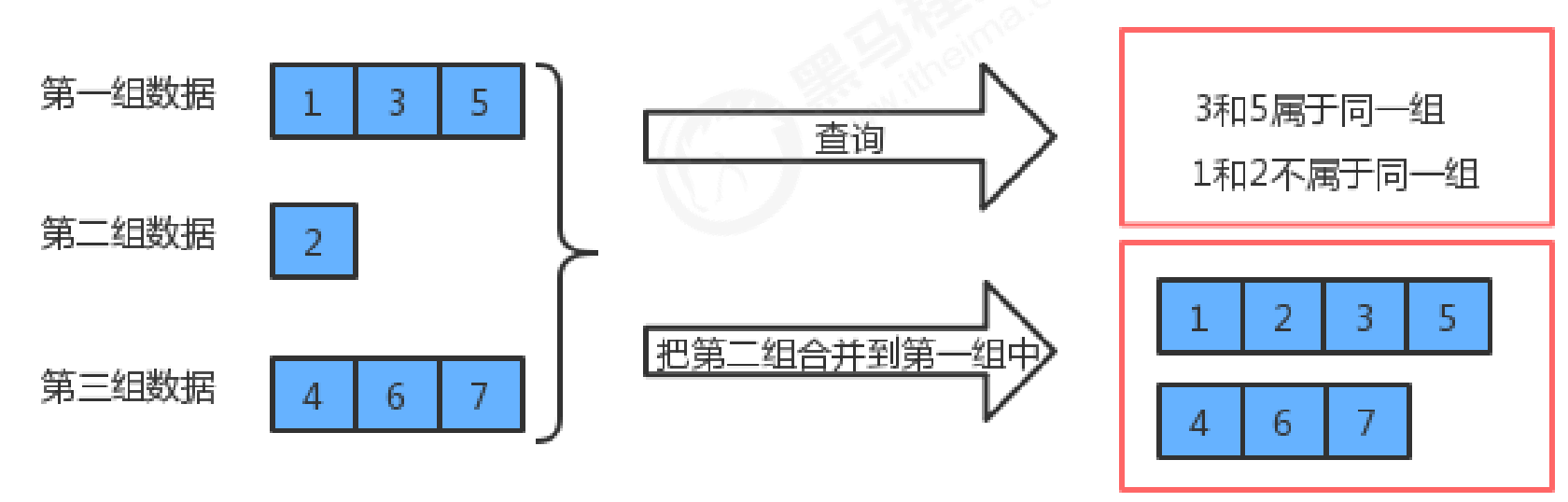
• Query whether element p and element q belong to the same group
• Merge the group of element p and element q

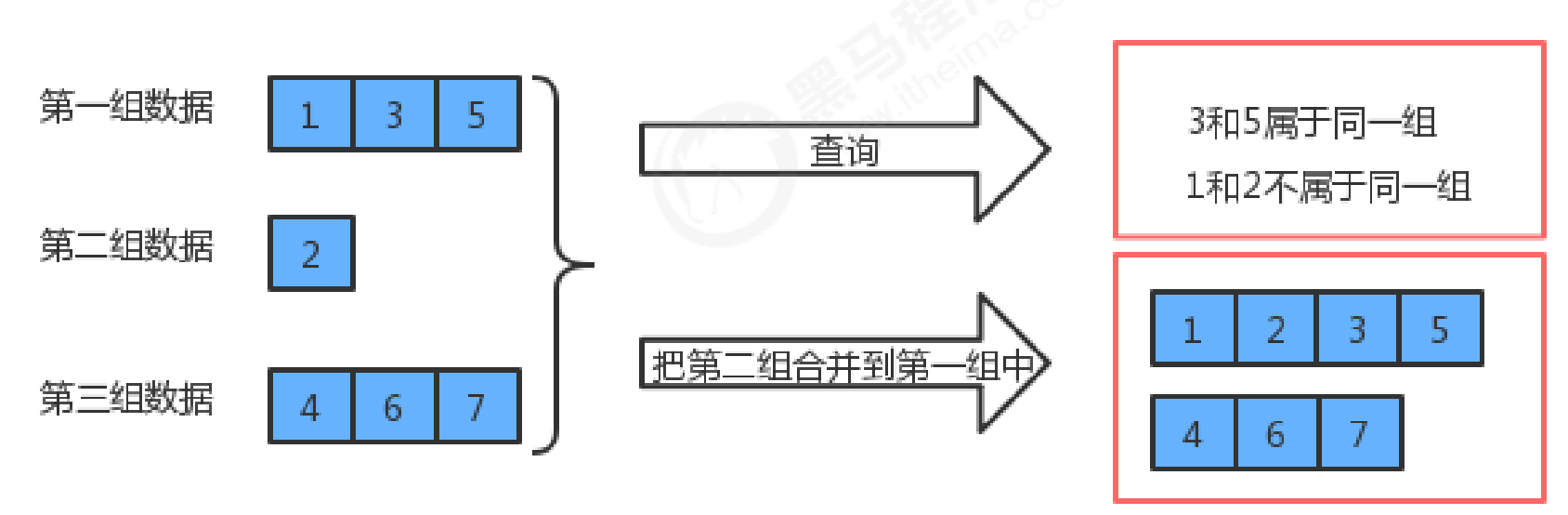
The parallel query set is also a tree structure, but this tree is different from the binary tree, red black tree and B tree we talked about earlier. The requirements of this tree are relatively simple:

1. Each element uniquely corresponds to a node;
2. Multiple elements in each group of data are in the same tree;
3. There is no connection between the tree corresponding to the data in one group and the tree corresponding to the data in another group;
4. Element has no rigid requirement of the child parent relationship in tree;

2. Implementation of parallel query API

package study.algorithm.uf;

public class UF {
  //Record the node element and the identification of the group in which the element is located
  private int[] eleAndGroup;
  //Record and check the number of data groups in the set
  private int count;

  //Initialize and query set
  public UF(int N) {
    //Number of initialization packets
    this.count = N;
    //Initialize eleAndGroup array
    this.eleAndGroup = new int[N];
    //Initialize the element in eleAndGroup and the identifier of its group, and make the index of eleAndGroup array as the element of each node in the query set,
    // And let the value at each index (the identification of the group in which the element is located) be the index
    for (int i = 0; i < eleAndGroup.length; i++) {
      eleAndGroup[i] = i;
    }
  }

  //How many groups are there in the current query set
  public int count() {
    return count;
  }

  //Identifier of the group in which the element p is located
  public int find(int p) {
    return eleAndGroup[p];
  }

  //Judge and check whether element p and element q in the set are in the same group
  public boolean connected(int p, int q) {
    return find(p) == find(q);
  }

  //Merge the group of p element and the group of q element
  public void union(int p, int q) {
    //Determine whether the elements p and q are already in the same group
    if (connected(p, q)) {
      return;
    }

    //Find the identifier of the group where p is located
    int pGroup = find(p);
    //Find the identifier of the group where q is located
    int qGroup = find(q);
    //Merge group: change the group identifier of all elements in p's group into the identifier of q's group
    for (int i = 0; i < eleAndGroup.length; i++) {
      if (eleAndGroup[i] == pGroup) {
        eleAndGroup[i] = qGroup;
      }
    }
    //Number of groups - 1
    this.count--;
  }
  
}

And search set test:

public static void main(String[] args) {
  UF uf = new UF(5);
  System.out.println("By default, the query set includes:"+uf.count()+"Groups");

  Scanner sc=new Scanner(System.in);
  while (true){
    System.out.println("Please enter the first element to merge:");
    int p = sc.nextInt();
    System.out.println("Please enter the second element to merge:");
    int q = sc.nextInt();

    if (uf.connected(p,q)){
      System.out.println(p+"Element and"+q+"The element is already in the same group");
      continue;
    }
    uf.union(p,q);
    System.out.println("The current query set also includes:"+uf.count()+"Groups");
  }
}

3. Improvement of joint search set algorithm

If each integer stored in the parallel query set represents a computer in a large computer network, we can detect whether two computers in the network are connected through connected(int p,int q)? If they are connected, they can communicate. If they are not connected, they cannot communicate. At this time, we can call union(int p,int q) to connect P and Q, so that the two computers can communicate.
Generally, for network data such as computers, we require that every two data in the network are connected, that is, we need to call the union method many times to connect all data in the network. In fact, we can easily conclude that if we want to connect all data in the network, we need to call the union method at least N-1 times, However, because our union method uses the for loop to traverse all elements, it is obvious that the time complexity of the merging algorithm we implemented before is O(N^2). If we want to solve large-scale problems, it is not appropriate, so we need to optimize the algorithm.

UF_Tree algorithm optimization

package study.algorithm.uf;

public class UF_Tree {
  //Record the node element and the identification of the group in which the element is located
  private int[] eleAndGroup;
  //Record and check the number of data groups in the set
  private int count;

  //Initialize and query set
  public UF_Tree(int N) {
    //Number of initialization packets
    this.count = N;
    //Initialize eleAndGroup array
    this.eleAndGroup = new int[N];
    //Initialize the element in eleAndGroup and the identifier of its group, and make the index of eleAndGroup array as the element of each node in the query set,
    // And let the value at each index (the identification of the group in which the element is located) be the index
    for (int i = 0; i < eleAndGroup.length; i++) {
      eleAndGroup[i] = i;
    }
  }

  //How many groups are there in the current query set
  public int count() {
    return count;
  }

  //Identifier of the group in which the element p is located
  public int find(int p) {
    while (true) {
      if (eleAndGroup[p] == p) {
        return p;
      }
      p = eleAndGroup[p];
    }
  }

  //Judge and check whether element p and element q in the set are in the same group
  public boolean connected(int p, int q) {
    return find(p) == find(q);
  }

  //Merge the group of p element and the group of q element
  public void union(int p, int q) {
    //Find the root node of the tree corresponding to the group of p and q elements
    int pRoot = find(p);
    int qRoot = find(q);

    if (pRoot == qRoot) {
      return;
    }
    eleAndGroup[pRoot] = eleAndGroup[qRoot];
    this.count--;
  }

}

Performance analysis after optimization

Our optimized algorithm union still needs to call the union method at least N-1 times if we want to connect all the data in the union query set. However, we find that there is no for loop in the union method, so the time complexity of the union algorithm changes from O(N^2) to O(N).
But this algorithm still has problems, because we modified not only the union algorithm, but also the find algorithm. When we modify the previous find algorithm
The inter complexity is O(1) in any case, but the modified find algorithm is O(N) in the worst case

The find method is invoked in the union method, so the time complexity of the union algorithm is still O(N^2) in the worst case.

Path compression

package study.algorithm.uf;

public class UF_Tree_Weighted {

  //Record the node element and the identification of the group in which the element is located
  private int[] eleAndGroup;
  //Record and check the number of data groups in the set
  private int count;
  //It is used to store the number of nodes saved in the tree corresponding to each root node
  private int[] sz;

  //Initialize and query set
  public UF_Tree_Weighted(int N) {
    //Number of initialization packets
    this.count = N;
    //Initialize eleAndGroup array
    this.eleAndGroup = new int[N];
    //Initialize the element in eleAndGroup and the identifier of its group, and make the index of eleAndGroup array as the element of each node in the query set,
    // And let the value at each index (the identification of the group in which the element is located) be the index
    for (int i = 0; i < eleAndGroup.length; i++) {
      eleAndGroup[i] = i;
    }
    //By default, the value at each index in sz is 1
    sz = new int[N];
    for (int i = 0; i < sz.length; i++) {
      sz[i] = 1;
    }
  }

  //How many groups are there in the current query set
  public int count() {
    return count;
  }

  //Identifier of the group in which the element p is located
  public int find(int p) {
    while (eleAndGroup[p] != p) {
      p = eleAndGroup[p];
    }
    return eleAndGroup[p];
  }

  //Judge and check whether element p and element q in the set are in the same group
  public boolean connected(int p, int q) {
    return find(p) == find(q);
  }

  //Merge the group of p element and the group of q element
  public void union(int p, int q) {
    //Find the root node of the tree corresponding to the group of p and q elements
    int pRoot = find(p);
    int qRoot = find(q);

    if (pRoot == qRoot) {
      return;
    }
    //Judge whether the tree corresponding to pRoot or qRoot is large, and finally merge the smaller trees into the larger trees
    if (sz[pRoot] < sz[qRoot]) {
      eleAndGroup[pRoot] = qRoot;
      sz[qRoot] += sz[pRoot];
    } else {
      eleAndGroup[qRoot] = pRoot;
      sz[pRoot] += sz[qRoot];
    }
    this.count--;
  }

}