Linear table

Linear table: a linear table is a finite sequence of n data elements with the same characteristics.

Related concepts:

• Precursor element, successor element
• Head node and tail node

Linear list classification: sequential list and linked list

1. Sequence table

Sequence table: sequence table is a linear table saved in the form of array in computer memory.

• Example: ArrayList

1.1 implementation of sequence table

package com.example.algorithm.linear;

public class SequenceList<T> {
  //An array of storage elements
  private T[] eles;
  //Record the number of elements in the current sequence table
  private int N;

  public SequenceList(int capacity) {
    //Initialize array
    this.eles = (T[]) new Object[capacity];
    //Initialization length
    this.N = 0;
  }

  public void clear() {
    this.N = 0;
  }

  public boolean isEmpty() {
    return N == 0;
  }

  public int length() {
    return N;
  }

  public T get(int i) {
    return eles[i];
  }

  public void insert(T t) {
    eles[N++] = t;
  }

  public void insert(int i, T t) {
    //First, move the i index and its subsequent elements backward one bit in turn
    for (int index = N; index > i; index--) {
      eles[index] = eles[index - 1];
    }
    //Then put the t element at the i index
    eles[i] = t;
    N++;
  }

  public T remove(int i) {
    T current = eles[i];
    for (int index = i; index < N - 1; index++) {
      eles[index] = eles[index + 1];
    }
    N--;
    return current;
  }

  public int indexOf(T t) {
    for (int i = 0; i < N; i++) {
      if (eles[i].equals(t)) {
        return i;
      }
    }
    return -1;
  }
}

1.2 traversal of sequence table

1. Let SequenceList implement Iterable interface and rewrite iterator method;
2. Provide an internal class SIterator inside the SequenceList, implement the Iterator interface, and rewrite hasNext method and next method;

@Override
public Iterator<T> iterator() {
	return new SIterator();
}

private class SIterator implements Iterator {
private int cursor;

public SIterator() {
  this.cursor = 0;
}

@Override
public boolean hasNext() {
  return cursor < N;
}

@Override
public Object next() {
  return eles[cursor++];
}
}

1.3 variable capacity of sequence table

  //Variable capacity method
  private void resize(int newSize) {
    T[] temp = eles;
    eles = (T[]) new Object[newSize];
    for (int i = 0; i < N; i++) {
      eles[i] = temp[i];
    }
  }
  
  public void insert(T t) {
    if (N == eles.length) {
      resize(2 * eles.length);
    }
    eles[N++] = t;
  }

  public void insert(int i, T t) {
    if (N == eles.length) {
      resize(2 * eles.length);
    }
    //First, move the i index and its subsequent elements backward one bit in turn
    for (int index = N; index > i; i--) {
      eles[index] = eles[index - 1];
    }
    //Then put the t element at the i index
    eles[i] = t;
    N++;
  }

  public T remove(int i) {
    T current = eles[i];
    for (int index = i; index < N - 1; index++) {
      eles[index] = eles[index + 1];
    }
    N--;
    if (N < eles.length / 4) {
      resize(eles.length / 2);
    }
    return current;
  }

1.4 time complexity of sequence table

• get(i): it is not difficult to see that no matter how large the number of data elements N is, the corresponding elements can be obtained only once eles[i], so the time complexity is O(1);
• Insert (int i, t, t): every time you insert, you need to move the elements behind I. with the increase of the number of elements N, the more elements are moved, and the time complexity is O(n);
• remove(int i): every time you delete, you need to move the elements behind the I position once. With the increase of the amount of data N, more elements are moved, and the time complexity is O(n);
• Because the bottom layer of the sequence table is implemented by an array, and the length of the array is fixed, the container expansion operation is involved in the process of operation. In this way, the time complexity of the sequence table in the use process is not linear. At some nodes that need to be expanded, the time will increase sharply, especially the more elements, the more obvious the problem is

1.5 ArrayLsit implementation

The bottom layer of the ArrayLsit set is the sequence table, which is implemented by array.

2. Linked list

Although the query of sequential table is fast and the time complexity is O(1), the efficiency of addition and deletion is relatively low, because each addition and deletion operation is accompanied by a large number of data elements. Is there a solution to this problem? Yes, we can use another storage structure to realize linear list and chain storage structure.
Linked list: it is a discontinuous and non sequential storage structure on the physical storage unit. Its physical structure cannot only represent the logical order of data elements. The logical order of data elements is realized through the pointer link order in the linked list. The linked list consists of a series of nodes (each element in the linked list is called a node), which can be generated dynamically at run time.

Node.java

public class Node<T> {
  //Storage element
  public T item;
  //Point to the next node
  public Node next;

  public Node(T item, Node next) {
    this.item = item;
    this.next = next;
  }
  
}

Generate linked list

public static void main(String[] args) {
  //Build node
  Node<Integer> first = new Node<>(11, null);
  Node<Integer> second = new Node<>(5, null);
  Node<Integer> third = new Node<>(8, null);
  Node<Integer> fourth = new Node<>(2, null);
  Node<Integer> fifth = new Node<>(74, null);
  //Generate linked list
  first.next = second;
  second.next = third;
  third.next = fourth;
  fourth.next = fifth;
}

2.1 one way linked list

Data field + pointer field

Implementation of one-way linked list

package com.example.algorithm.linear;

public class LinkList<T> {
  //Record header node
  private Node head;
  //Record the length of the linked list
  private int length;

  //Node class
  private class Node {
    //Store data
    T item;
    //Next node
    Node next;

    public Node(T item, Node next) {
      this.item = item;
      this.next = next;
    }
  }

  public LinkList() {
    //Initialize header node
    this.head = new Node(null, null);
    //Number of initialization elements
    this.length = 0;
  }

  public void clear() {
    this.head = null;
    this.length = 0;
  }

  public int size() {
    return length;
  }

  public boolean isEmpty() {
    return length == 0;
  }

  public T get(int i) {
    //Through the loop, start from the node and look back, i times in turn, you can find the corresponding element
    Node n = head.next;
    for (int index = 0; index < i; index++) {
      n = n.next;
    }
    return n.item;
  }

  public void insert(T t) {
    //Find the last current node
    Node n = head;
    while (n.next != null) {
      n = n.next;
    }
    //Create a new node and save the element t
    Node newNode = new Node(t, null);
    //Make the current last node point to the new node
    n.next = newNode;
    //Number of elements + 1
    length++;
  }

  public void insert(T t, int i) {
    //Find the previous node at position i
    Node pre = head;
    for (int index = 0; index < i; index++) {
      pre = pre.next;
    }
    //Find i location node
    Node curr = pre.next;
    //Create a new node, and the new node needs to point to the node at the original i location
    Node newNode = new Node(t, curr);
    //The previous node in the original i position can point to the new node
    pre.next = newNode;
    //Number of elements + 1
    length++;
  }

  public T remove(int i) {
    //Find the previous node at position i
    Node pre = head;
    for (int index = 0; index < i; index++) {
      pre = pre.next;
    }
    //Find the node at position i
    Node curr = pre.next;
    //Find the next node at position i
    Node nextNode = curr.next;
    //The previous node points to the next node
    pre.next = nextNode;
    //Number of elements - 1
    length--;
    return curr.item;
  }

  public int indexOf(T t) {
    Node n = head;
    for (int i = 0; n.next != null; i++) {
      n = n.next;
      if (n.item.equals(t)) {
        return i;
      }
    }
    return -1;
  }
}

Traversal of one-way linked list

  @Override
  public Iterator<T> iterator() {
    return new Itr();
  }

  private class Itr implements Iterator {
    private Node n;

    public Itr() {
      this.n = head;
    }

    @Override
    public boolean hasNext() {
      return n.next != null;
    }

    @Override
    public Object next() {
      n = n.next;
      return n.item;
    }
  }

2.2 bidirectional linked list

Example: LinkedList: implemented using a two-way linked list

One data field + two pointer fields

Implementation of bidirectional linked list

package com.example.algorithm.linear;

import java.util.Iterator;

public class TwoWayLinkList<T> implements Iterable<T> {
  //First node
  private Node head;
  //Last node
  private Node last;
  //Length of linked list
  private int length;

  @Override
  public Iterator iterator() {
    return new Itr();
  }

  private class Itr implements Iterator<T> {
    private Node n;

    public Itr() {
      this.n = head;
    }

    @Override
    public boolean hasNext() {
      return n.next != null;
    }

    @Override
    public T next() {
      n = n.next;
      return n.item;
    }
  }

  //Node class
  private class Node {
    //Store data
    public T item;
    //Point to previous node
    public Node pre;
    //Point to the next node
    public Node next;

    public Node(T item, Node pre, Node next) {
      this.item = item;
      this.pre = pre;
      this.next = next;
    }
  }

  public TwoWayLinkList() {
    //Initialize head node and tail node
    this.head = new Node(null, null, null);
    this.last = null;
    //Number of initialization elements
    this.length = 0;
  }

  public void clear() {
    this.head.next = null;
    this.last = null;
    this.length = 0;
  }

  public int size() {
    return length;
  }

  public boolean isEmpty() {
    return length == 0;
  }

  public T getFirst() {
    return isEmpty() ? null : head.next.item;
  }

  public T getLast() {
    return isEmpty() ? null : last.item;
  }

  public void insert(T t) {
    if (isEmpty()) {
      last = new Node(t, head, null);
      head.next = last;
    } else {
      Node oldLast = last;
      Node newNode = new Node(t, oldLast, null);
      oldLast.next = newNode;
      last = newNode;
    }
    length++;
  }

  public void insert(T t, int i) {
    Node pre = head;
    for (int index = 0; index < i; index++) {
      pre = pre.next;
    }
    Node next = pre.next;
    Node newNode = new Node(t, pre, next);
    pre.next = newNode;
    next.pre = newNode;
    length++;
  }

  public T get(int i) {
    Node n = head.next;
    for (int index = 0; index < i; index++) {
      n = n.next;
    }
    return n.item;
  }

  public int indexOf(T t) {
    Node n = head;
    for (int i = 0; n.next != null; i++) {
      n = n.next;
      if (n.next.equals(t)) {
        return i;
      }
    }
    return -1;
  }

  public T remove(int i) {
    Node pre = head;
    for (int index = 0; index < i; index++) {
      pre = pre.next;
    }
    Node curr = pre.next;
    Node nextNode = curr.next;
    pre.next = nextNode;
    nextNode.pre = pre;
    length--;
    return curr.item;
  }
}

2.3 application scenario of linked list

1. Single linked list inversion

1. Recursive inversion

The recursive inversion method inverts the subsequent nodes before inverting the current node. In this way, we start from the beginning node and go deep layer by layer until the end node begins to reverse the direction of the pointer field. In short, it starts from the tail node,

public static Node reverse(Node head) {
  if (head == null || head.next == null) {
    return head;
  }
  Node pre = reverse(head.next);
  head.next.next = head;
  head.next = null;
  return pre;
}

2. Ergodic inversion

The recursive inversion method reverses the direction of the pointer field from back to front, while the traversal inversion method reverses the direction of the pointer field of each node from front to back.

The basic idea is: cache the next node cur.getNext() of the current node cur to temp, and then change the current node pointer to the previous node pre. In other words, before reversing the current node pointer, the pointer field of the current node is temporarily saved with tmp for next use

public static Node reverse(Node head) {
  if (head == null || head.next == null) {
    return head;
  }
  Node pre = null;
  Node next = null;
  while (head != null) {
    next = head.next;
    head.next = pre;
    pre = head;
    head = next;
  }
  return pre;
}

2. Speed pointer

Speed pointer refers to defining two pointers, and the movement speed of the two pointers is slow one by one, so as to create the desired difference. This difference can enable us to find the corresponding node on the linked list. In general, the moving step of the fast pointer is twice that of the slow pointer

2.1 intermediate value problem

As shown in the following figure, at first, the slow and fast pointers point to the first node of the linked list, then slow moves one pointer at a time, and fast moves two pointers at a time.

/**
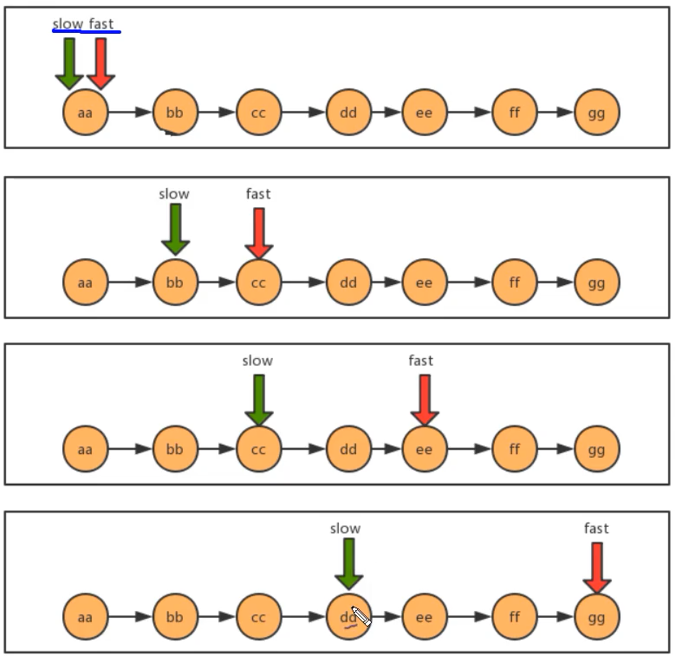
 * @param first The first node of the linked list
 * @return The value of the intermediate node of the linked list
 */
public static String getMid(Node<String> first) {
  //Define two pointers
  Node<String> fast = first;
  Node<String> slow = first;
  //Use two pointers to traverse the linked list. When the node pointed to by the fast pointer has no next node, it ends; At the end, the node pointed to by the slow pointer is the intermediate value
  while (fast != null && fast.next != null) {
    fast = fast.next.next;
    slow = slow.next;
  }

  return slow.item;
}

2.2 is there a ring problem in the one-way linked list

  /**
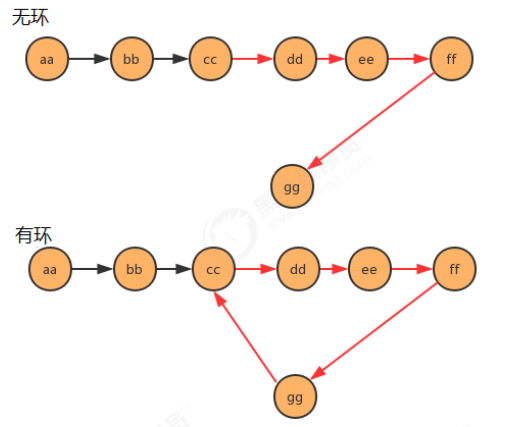
   * Determine whether there are links in the linked list
   *
   * @param first First node of linked list
   * @return ture Is ring, false is acyclic
   */
  public static boolean isCircle(Node<String> first) {
    //Define speed pointer
    Node<String> fast = first;
    Node<String> slow = first;
    //Traverse the linked list. If the speed pointer points to the first node, it proves that there is a ring
    while (fast != null && fast.next != null) {
      fast = fast.next.next;
      slow = slow.next;
      if (fast.equals(slow)) {
        return true;
      }
    }
    return false;
  }

2.3 problem of linked list entry

When the fast and slow pointers meet, we can judge that there is a ring in the linked list. At this time, reset a new pointer to the starting point of the linked list, and the step size is 1 as the slow pointer. Then the place where the slow pointer meets the "new" pointer is the entrance of the ring. Proving this conclusion involves the knowledge of number theory, which is omitted here and only about realization.

  /**
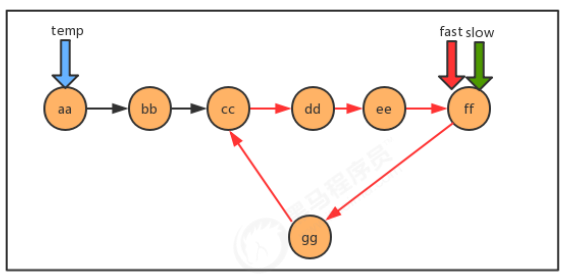
   * Find the entry node of a ring in a linked list
   *
   * @param first First node of linked list
   * @return Entrance node of ring
   */
  public static Node getEntrance(Node<String> first) {
    //Define speed pointer
    Node<String> fast = first;
    Node<String> slow = first;
    Node<String> temp = null;
    //Traverse the linked list and find the ring first (the fast and slow pointers meet). Prepare a temporary pointer to the first node of the linked list and continue to traverse until the slow pointer meets the temporary pointer. Then the node pointed to when meeting is the entrance of the ring.
    while (fast != null && fast.next != null) {
      fast = fast.next.next;
      slow = slow.next;
      //Judge whether the speed pointer meets
      if (fast.equals(slow)) {
        temp = first;
        break;
      }
    }
    while (temp != null) {
      temp = temp.next;
      slow = slow.next;
      if (temp.equals(slow)) {
        break;
      }
    }
    return temp;
  }

3. Circular linked list

Circular linked list, as the name suggests, the whole linked list should form a circular ring. In a one-way linked list, the pointer of the last node is null and does not point to any node, because there is no next element. To realize the circular linked list, we only need to make the pointer of the last node of the one-way linked list point to the head node.

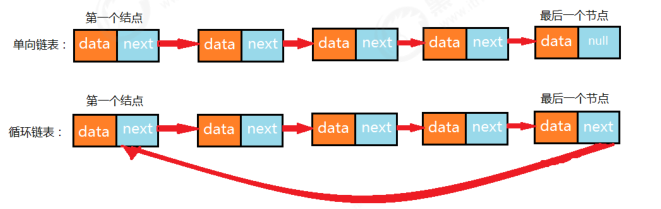
4. Joseph problem

Circular linked list to solve Joseph problem

Problem Description:
It is said that after the Romans occupied jotapat, 39 Jews hid in a cave with Joseph and his friends. 39 Jews decided to die rather than be caught by the enemy, so they decided to commit suicide. 41 people lined up in a circle. The first person counted off from 1, and then, if someone counted off to 3, Then this person must commit suicide, and then his next person starts counting again from 1 until everyone commits suicide. However, Joseph and his friends did not want to comply. So Joseph asked his friend to pretend to obey first. He arranged his friend and himself in the 16th and 31st positions, so as to escape the death game.

Problem conversion:
41 people sit in a circle. The first person is numbered 1, the second person is numbered 2, and the nth person is numbered n.

1. The person with number 1 starts to count back from 1, and the person with number 3 quits the circle;
2. The next person starting from the person who quit will count off from 1 again, and so on;
3. Find the number of the person who quit last.

package study.algorithm.sort;

public class Joseph {

  public static void main(String[] args) {
    JosephMethod(41, 3);

  }

  public static void JosephMethod(int totalNum, int countNum) {
    //1. Building a one-way circular linked list
    //First is used to record the first node, and pre records the previous node
    Node<Integer> pre = null;
    Node<Integer> first = null;
    for (int i = 1; i <= totalNum; i++) {
      if (i == 1) {
        first = new Node<>(i, null);
        pre = first;
        continue;
      }
      //If not the first node
      Node newNode = new Node(i, null);
      pre.next = newNode;
      pre = newNode;
      //If it is the last node, you need to make the next node of the last node become first and a circular linked list
      if (i == totalNum) {
        pre.next = first;
      }
    }
    //2. count counter is required to simulate the number of alarms
    int count = 0;
    //3. Traversal circular linked list
    //Record the nodes obtained in each traversal, starting from the first node by default
    Node<Integer> n = first;
    //Record the previous node of the current node
    Node<Integer> before = null;
    while (n != n.next) {
      //Analog alarm
      count++;
      if (count == totalNum) {
        before.next = n.next;
        System.out.print(n.item + ",");
        count = 0;
      } else {
        before = n;
      }
      n = n.next;
    }
    //Print last element
    System.out.print(n.item);

  }

  private static class Node<T> {
    public T item;
    public Node next;

    public Node(T item, Node next) {
      this.item = item;
      this.next = next;
    }
  }
}

3. Stack

Linear tables have two special data structures:

Stack

• Sequential stack
  • Two stack shared space
• Chain stack

queue

• Sequential queue
  • Circular queue
• Chain queue

Stack: first in, then out. A special linear table that can only be inserted and deleted at one end.

Stack can be realized by chain data structure or sequential data structure

Implementation of stack

package com.example.algorithm.linear;
import java.util.Iterator;

public class Stack<T> implements Iterable<T> {
  //Record first node
  private Node head;
  //Number of elements in the stack
  private int N;

  @Override
  public Iterator<T> iterator() {
    return new Itr();
  }

  private class Itr implements Iterator<T> {
    private Node n;

    public Itr() {
      this.n = head;
    }

    @Override
    public boolean hasNext() {
      return n.next != null;
    }

    @Override
    public T next() {
      n = n.next;
      return n.item;
    }
  }

  private class Node {
    public T item;
    public Node next;

    public Node(T item, Node next) {
      this.item = item;
      this.next = next;
    }
  }

  public Stack() {
    this.head = new Node(null, null);
    this.N = 0;
  }

  public boolean isEmpty() {
    return N == 0;
  }

  public int size() {
    return N;
  }

  //Stack pressing
  public void push(T t) {
    //Find the first node pointed to by the first node
    Node oldFirst = head.next;
    //Create a new node
    Node newNode = new Node(t, null);
    //Let the first node point to the new node
    head.next = newNode;
    //Let the new node point to the original first node
    newNode.next = oldFirst;
    //Number of elements + 1
    N++;
  }

  //Bomb stack
  public T pop() {
    //Find the first node pointed to by the first node
    Node oldFirst = head.next;
    //Let the first node point to the next node of the original first node
    if (oldFirst == null) {
      return null;
    }
    head.next = oldFirst.next;
    //Number of elements - 1
    N--;
    return oldFirst.item;
  }

}

Array implementation stack

package com.example.algorithm.linear;

import java.util.Iterator;

public class Stack2<T> implements Iterable<T> {
  private T[] items;
  private int N;

  public Stack2(int capacity) {
    this.items = (T[]) new Object[capacity];
    this.N = 0;
  }

  public boolean isEmpty() {
    return N == 0;
  }

  public int size() {
    return N;
  }

  public void push(T t) {
    if (N == items.length) {
      resize(2 * items.length);
    }
    items[N++] = t;
  }

  public T pop() {
    T pop = items[--N];
    items[N] = null;
    if (N < items.length / 4) {
      resize(items.length / 2);
    }
    return pop;
  }

  private void resize(int capacity) {
    T[] temp = items;
    items = (T[]) new Object[capacity];
    for (int i = 0; i < N; i++) {
      items[i] = temp[i];
    }
  }

  @Override
  public Iterator<T> iterator() {
    return new Itr();
  }

  private class Itr implements Iterator<T> {
    private int cursor;

    public Itr() {
      this.cursor = 0;
    }

    @Override
    public boolean hasNext() {
      return cursor < N;
    }

    @Override
    public T next() {
      return items[cursor++];
    }
  }
}

Application of stack

1. Bracket matching problem

Problem Description:

Given a string, it may contain"()"Parentheses and other characters, write a program to check whether the parentheses in the string appear in pairs.
For example:
	"(Shanghai)(Chang'an)": Correct match
	"Shanghai((Chang'an))": Correct match
	"Shanghai(Chang'an(Beijing)(Shenzhen)Nanjing)":Correct match
	"Shanghai(Chang'an))": Wrong match
	"((Shanghai)Chang'an": Wrong match

  /**
   * Determine whether the parentheses in str match
   *
   * @param str A string of parentheses
   * @return Returns true if there is a match, and false if there is no match
   */
  public static boolean isMatch(String str) {
    String[] strings = str.split("");
    Stack<String> stack = new Stack<>();
    for (String string : strings) {
      if ("(".equals(string)) {
        stack.push(str);
      } else if (")".equals(string)) {
        String pop = stack.pop();
        if (pop == null) {
          return false;
        }
      }
    }
    return stack.size() == 0;
  }

2. Inverse Polish expression evaluation problem

Infix expression
Infix expressions are expressions used in our daily life, such as 1 + 3 * 2,2 - (1 + 3), etc. the characteristic of infix expressions is that binary operators are always placed between two operands.
Inverse Polish expression (suffix expression)
The characteristic of suffix expression: the operator is always placed after the operand associated with it.

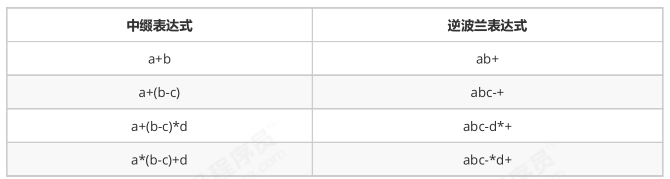
demand
Given an array representation of an inverse Polish expression containing only four operations of addition, subtraction, multiplication and division, the result of the inverse Polish expression is obtained.

package com.example.algorithm.linear;

public class ReversePolishNotation {
  public static void main(String[] args) {
    //The inverse Polish expression of infix expression 3 * (17-15) + 18 / 6 is as follows
    String[] notation = {"3", "17", "15", "-", "*", "18", "6", "/", "+"};
    int result = calculate(notation);
    System.out.println("The result of the inverse Polish expression is:" + result);
  }

  /**
   * @param notaion Array representation of inverse Polish expressions
   * @return Calculation results of inverse Polish expression
   */
  public static int calculate(String[] notaion) {
    Stack<Integer> operators = new Stack<>();
    for (String s : notaion) {
      Integer o1 = 0;
      Integer o2 = 0;
      switch (s) {
        case "+":
          o1 = operators.pop();
          o2 = operators.pop();
          operators.push(o2 + o1);
          break;
        case "-":
          o1 = operators.pop();
          o2 = operators.pop();
          operators.push(o2 - o1);
          break;
        case "*":
          o1 = operators.pop();
          o2 = operators.pop();
          operators.push(o2 * o1);
          break;
        case "/":
          o1 = operators.pop();
          o2 = operators.pop();
          operators.push(o2 / o1);
          break;
        default:
          operators.push(Integer.parseInt(s));
          break;
      }
    }
    return operators.pop();
  }
}

Prefix, suffix, infix expression

Example:

Infix expression: a+b*c+(d*e+f)*g
 Prefix expression:++a*bc*+*defg
 Suffix expression: abc*+de*f+g*+

Infix expressions are convenient for people to understand and calculate, but prefix and suffix expressions are more convenient for computer operation

There are three ways to convert infix to prefix and suffix:

1. Stack based algorithm (relatively complex, for computer implementation)

2. Bracket method

3. Semantic tree

Bracket method:

1. Parenthesize all arithmetic units according to the priority of the operator

   ((a+(b*c))+(((d*e)+f)*g))
   

2. Convert to prefix and suffix expressions

   • Prefix: move the operation symbol to the front of the corresponding bracket
   • Suffix: move the operation symbol after the corresponding bracket

Semantic tree

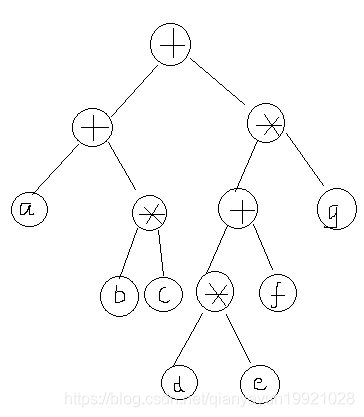
• Infix: first left, then middle, then right
• Prefix: first middle, then left, then right
• Suffix: first left, then right, in

Two stack shared space

For the array implementation stack, if it is two stacks with the same data type, the method of using both ends of the array as the bottom of the stack can be used to make the two stacks share data, so as to maximize the space of the array.

• The shared space of two stacks is usually when the space requirements of two stacks are opposite, that is, one stack is growing and the other stack is shortening. This makes sense to use two stacks of shared space.

package com.example.algorithm.linear;

import org.omg.CORBA.Object;

public class TwoStack<T> {
  private T[] items;
  private int n1;
  private int n2;

  public TwoStack(int capacity) {
    this.items = (T[]) new Object[capacity];
    this.n1 = 0;
    this.n2 = capacity - 1;
  }

  public void push(T t, int stackNum) {
    if (stackNum != 1 && stackNum != 2 || n1 == n2) {
      return;
    }
    if (stackNum == 1) {
      items[n1++] = t;
    } else {
      items[n2--] = t;
    }
  }

  public T pop(int stackNum) {
    if (stackNum != 1 && stackNum != 2) {
      return null;
    }
    if (stackNum == 1) {
      if (n1 == 0) {
        return null;
      } else {
        return items[--n1];
      }
    } else {
      if (n2 == items.length - 1) {
        return null;
      } else {
        return items[++n2];
      }
    }
  }


}

4. Queue

Queue: first in first out. It is a special linear table that can only be inserted at one end and deleted at the other end.

That is, it can be realized by sequential data structure or chain data structure

Implementation of queue

package com.example.algorithm.linear;

import java.util.Iterator;

public class Queue<T> implements Iterable<T> {
  //Record first node
  private Node head;
  //Record the last node
  private Node last;
  //Record the number of elements in the queue
  private int N;

  @Override
  public Iterator<T> iterator() {
    return new Itr();
  }

  private class Itr implements Iterator<T> {
    private Node n;

    public Itr() {
      this.n = head;
    }

    @Override
    public boolean hasNext() {
      return n.next != null;
    }

    @Override
    public T next() {
      n = n.next;
      return n.item;
    }
  }

  private class Node {
    public T item;
    public Node next;

    public Node(T item, Node next) {
      this.item = item;
      this.next = next;
    }
  }

  public Queue() {
    this.head = new Node(null, null);
    this.last = null;
    this.N = 0;
  }

  public boolean isEmpty() {
    return N == 0;
  }

  public int size() {
    return N;
  }

  //Insert element t into queue
  public void enqueue(T t) {
    if (last == null) {
      last = new Node(t, null);
      head.next = last;
    } else {
      Node oldLast = last;
      last = new Node(t, null);
      oldLast.next = last;
    }
    N++;
  }

  //Take an element from the queue
  public T dequeue() {
    if (isEmpty()) {
      return null;
    }
    Node oldFirst = head.next;
    head.next = oldFirst.next;
    N--;
    return oldFirst.item;
  }
}

Circular queue related problems (C language, array implementation)

• Front points to the queue head element, and rear points to the next position of the queue tail element (in Java, that is, front=0,rear=arr.length)
  • When the queue is empty, front=rear=0

Circular queue

When the queue "false overflow", it will start from the beginning and end to end. That is, in case of false overflow, rear=1

At this point, the problem comes: when the queue is empty, front=rear, then when the queue is full, front=rear. How to judge whether the team is full or empty?

1. Method 1: set a variable flag. When front=rear and flag=0, the queue is empty; When front=rear, flag=1, the queue is full
2. Method 2: modify the team full condition and reserve an element space. That is, when the queue is full, there is another free cell in the array. That is, front+rear+1==queueSize
   • (rear+1)%queueSize==front
   • General queue calculation formula: (rear front + queuesize)% queuesize