Data structure and algorithm foundation - Go language version - 2. Stack

This paper will systematically introduce the structure and characteristics of stack, and give how to realize the stack of sequential structure and chain structure in go language. Finally, the sequential stack is used to complete several exercises.

1, Definition and characteristics of stack?

Definition of stack: stack is a linear table that is restricted to insert and delete operations only at the end of the table
Stack features: first in first out, last in first out

2, Implementation of stack

2.1 sequence stack

2.1.1 structure definition of sequence stack

The container structure of the stack is designed as follows

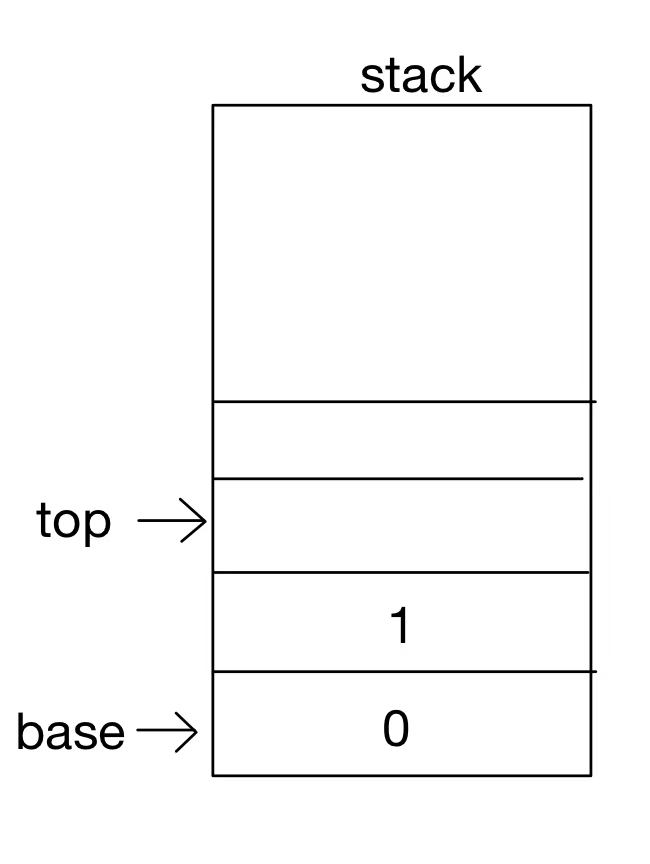
code implementation

type stack struct{
    top int  // Points to the next position of the top element of the stack
    base int // Always point to the bottom of the stack
    container []int //Dynamic capacity expansion can be achieved by using slices
    length int // Record the number of elements in the current stack
    size int // Record the maximum capacity of the current stack
}

2.1.2 initialization of sequence stack

func initStack(size int)*stack{
    return &stack{
        top:0,
        base:0,
        container:make([]int,size,size), //There are two methods: one is to define the length as 0 and append it with the append() function when entering the stack, but it is troublesome to erase the value of the underlying array when bouncing the stack. The other is to define the length as size and directly assign the index value when entering the stack
        length:0,
        size:size,
    }
}

2.1.3 judge whether the stack is empty or full

func (s *stack)isValid()bool{
    return s.length==0
}

func (s *stack)isFull()bool{
    return s.length==s.size
}

2.1.4 stacking

func (s *stack)push(data int)error{
    if s.isFull(){
        return errors.New("the stack is full,can not push any value\n")
    }
    s.container[s.top]=data //Append elements to the end of the table (i.e. the top of the stack)
    s.top++ // Keep top pointing to the next position of the top element of the stack
    s.length++ 
    return nil
}

2.1.5 out of stack

func (s *stack)pop()(int,error){
    if s.isValid(){
        return -1,errors.New("the stack is valid,can not pop any value\n")
    }
    s.top--  // First point top to the current stack top element
    s.length-- 
    return s.container[s.top],nil
}

2.1.6 preview stack top elements

func (s *stack)peek()string{
    return s.container[top-1]
}

2.2 chain stack

2.2.1 structure definition of chain stack

type sNode struct{
    data int
    next *sNode
}

func newSNode(data int)*sNode{
    return &sNode{
        data:data,
        next:nil,
    }
}

type lStack struct{
    top *sNode //The top pointer points to the chain header node and does not store data. The header node always points to the top element of the stack
    length int
}

2.2.2 initialization of chain stack

// Initialization of chain stack
func initLStack()*lStack{
    return &lStack{
        top:newSNode(-1),
        length:0,
    }
}

2.1.3 stack empty judgment

// Judge whether the chain stack is empty
func (ls *lStack)isValid()bool{
    return ls.length==0
}

2.2.4 stack (the header insertion method of linked list is used here)

thinking
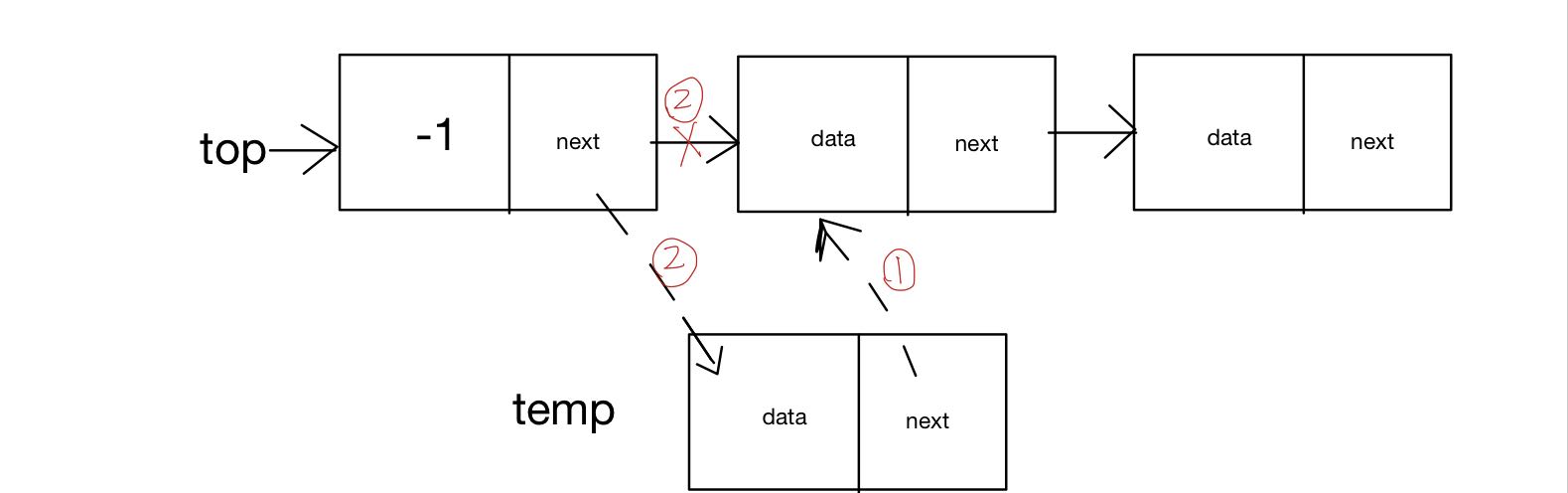
The code is implemented as follows

// Chain stack
func (ls *lStack)push(data int){
    temp := newSNode(data)
    temp.next =ls.top.next
    ls.top.next=temp
    ls.length++
}

2.2.5 Out of stack

thinking
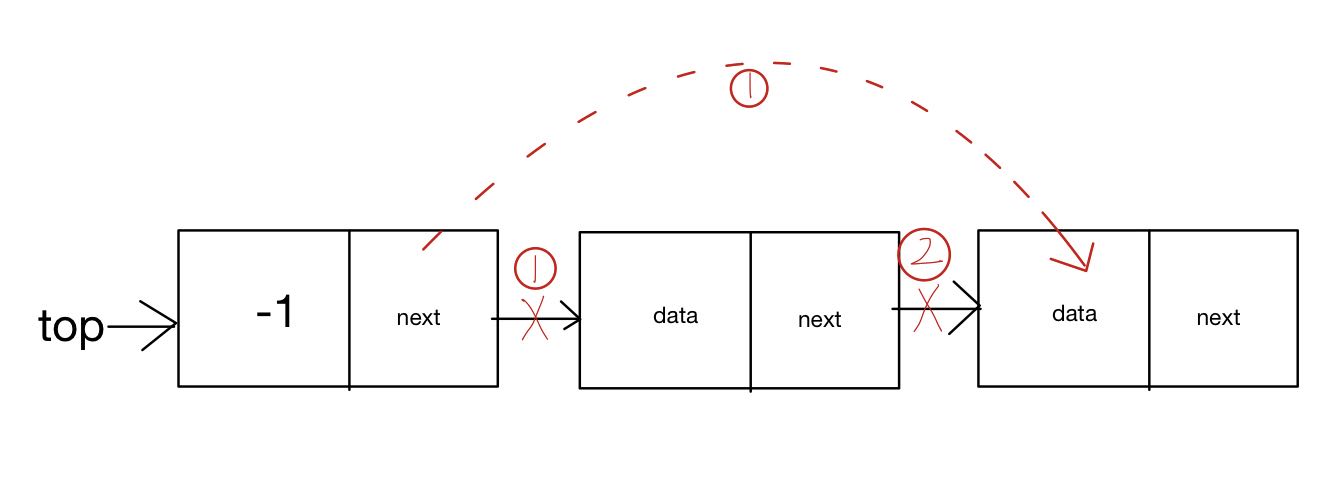
The code is implemented as follows

// Chain stack out of stack
func (ls *lStack)pop()(int,error){
    if ls.isValid(){
        return -1,errors.New("the stack is valid,can not pop any value\n")
    }
    result := ls.top.next
    ls.top.next = result.next
    result.next = nil
    ls.length--
    return result.data,nil
    
}

3, Practice

3.1 hexadecimal conversion, design a function. It is required to input a hexadecimal number, which can be output and converted into the corresponding hexadecimal number.

thinking

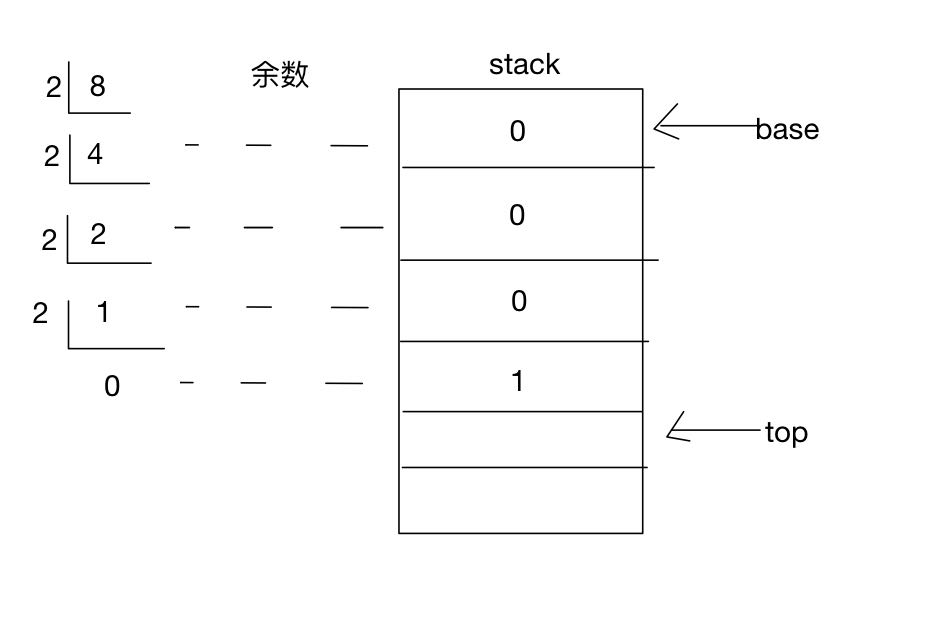
The code is implemented as follows

const(
    Binary = 2
    Octcal = 8
    Hex = 16
)


// The default input data range of this function is [0255], and the conversion to A.B, C, D and e when hexadecimal is greater than 9 is not considered
func trans(data int,convert int)[]int{
    s := initStack(8)
    result := make([]int,0,8)
    remainder := data % convert // Mod 
    for data != 0{ // Finally, the data will be divided to 0
        s.push(remainder) // Stack remainder
        data = data /  convert // Update data
        remainder = data % convert
    }
    
    length := s.length
    for i:=0 ; i < length ; i++{
        result = append(result,s.pop())
    }
    return result
}

3.2 bracket matching: enter any number of strings containing only brackets, and the function can judge whether the number and type of brackets in the string match

thinking
- Encountered left parenthesis' (',' [',' {'on the stack
- If the right bracket is encountered, pop the stack and perform symbol matching at the same time. If it does not match, false is returned. If the stack is empty, there are too many right brackets
- After scanning the string, judge whether the stack is not empty. If it is not empty, it indicates that there are more left parentheses in the stack