This example completes simple mathematical statistics work by simulating some random numbers as an experience of later data analysis
Random walk: randomly generate 1 or - 1 random number to imitate a person's advance or retreat
In this environment, some statistical work is carried out
Random walk
- Do some preparations for the homepage
import numpy as np # Import random number library # Frequency of stroll num = 1000
- Generate some random numbers needed
# n walks are generated, and the data is 0 or 1 draws = np.random.randint(0, 2, size=num) # Replace the part with data 0 with - 1 steps = np.where(draws>0, 1, -1) # Track by accumulation walk = steps.cumsum() # Output footstep record print('Footprints:{}'.format(walk)) ''' [-1 0 1 0 1 2 1 0 -1 0 -1 0 -1 0 -1 -2 -1 -2 -1 0 1 2 3 2 1 0 1 2 1 0 ... 67 68 67 68 67 68] '''
- Count the longest distance forward and backward
# Count the maximum distance of forward and backward in the process of walking max_y = walk.max() max_x = walk.argmax() print('stay{}In the walk, the{}The furthest distance to step forward:{}'.format(num,max_x,max_y)) '''Step 909 of the 1000 walks: 72''' min_y = walk.min() min_x = walk.argmin() print('stay{}In the walk, the{}Step back the farthest distance:{}'.format(num,min_x,min_y)) '''Step 15 of the 1000 walks back the farthest distance:-2'''
- Statistics of data meeting certain conditions
# Index with a distance of 30 from the origin during the statistical walk greater_or_equal_30 = np.abs(walk)>=30 print('stay{}The total number of walks over 30 is:{}'.format(num,greater_or_equal_30.sum())) '''The total number of walks over 30 in 1000 is: 413''' # Index first reached 30 first_30 = greater_or_equal_30.argmax() print('stay{}Index with the first distance more than 30 in the walk:{}'.format(num,first_30)) '''Index of first distance over 30 in 1000 walks: 551''' value = np.where(greater_or_equal_30==True) print('Index over 30 in 1000 walks:{}'.format(value)) ''' //Index over 30 in 1000 walks: (array ([551, 552, 553, 563, 564, 565, 567, 568, 569, 575, 576, 577, 578,... 970, 971, 972, 973, 974, 975, 976, 977, 978, 979, 981, 982, 983, 984, 985, 986, 987, 988, 989990, 991, 992, 993, 994, 996, 997, 998, 999]) '''
If the above data is too ugly, we can use matplotlib to draw the graph to make the data more intuitive
- Import the library first. Please install it if there is no library
python2:
pip install matplotlib
python3:
pip3 install matplotlib
Drawing graphics
# Import import matplotlib.pyplot as plt # Drawing library # Drawing related figures x = np.linspace(0, 1000, num=1000) y1 = walk plt.figure() plt.title('random walk') # Draw the footprints of walking plt.plot(x, y1, color='yellow', linewidth=1, label='walk step') y2 = np.ones(1000)*30 y3 = -y2 # Draw + - 30 lines plt.plot(x, y2, color='r', linewidth=1, linestyle='--', label='+30') plt.plot(x, y3, color='g', linewidth=1, linestyle='--', label='-30') # Draw keys plt.scatter([max_x,min_x,first_30], [max_y,min_y,walk[first_30]], s=30, color=['r','g','b']) # Add annotation # Maximum distance coordinate plt.annotate( 'max:({},{})'.format(max_x,max_y), xy = (max_x,max_y), xycoords = 'data', xytext = (-20, +20), textcoords='offset points', fontsize = 8, arrowprops=dict(arrowstyle='->', connectionstyle="arc3,rad=.2") ) # Minimum distance coordinate plt.annotate( 'min:({},{})'.format(min_x,min_y), xy = (min_x,min_y), xycoords = 'data', xytext = (-20, +20), textcoords='offset points', fontsize = 8, arrowprops=dict(arrowstyle='->', connectionstyle="arc3,rad=.2") ) # Coordinates of the first 30 distance if walk[first_30]==30: plt.annotate( 'first arrive to 30:({},{})'.format(first_30, walk[first_30]), xy=(first_30, walk[first_30]), xycoords='data', xytext=(-20, +20), textcoords='offset points', fontsize=8, arrowprops=dict(arrowstyle='->', connectionstyle="arc3,rad=.2") ) # Legend plt.legend(loc='best') # Display image plt.show()

Multiple random walks
# To simulate multiple random walks, 15 sets of random numbers are generated here nwalks = 15 nsteps = 1000 # Only slightly modify the parameter size draws = np.random.randint(0, 2, size=(nwalks, nsteps)) steps = np.where(draws>0, 1, -1) walks = steps.cumsum(axis=1) # Lateral accumulation
- Statistics related data
# The longest distance max_distance = walks.max(axis=1) print('{}In the group of random walking, the farthest distance was:{}'.format(nwalks,max_distance)) '''15 In the group of random walking, the farthest distance was:[26 32 24 44 36 65 40 33 46 74 31 25 28 43 48]''' # More than 30 from the origin values = np.abs(walks) >= 30 # Whether there is a distance of more than 30 in each group's random walk hits30 = np.any(values, axis=1) # Horizontal search print('{}Group random walk, total{}Group with a distance of more than 30, specifically:{}'.format(nwalks,hits30.sum(),hits30)) '''15 In group A, there were 11 groups with a distance of more than 30[False True False True True True True True True True True False False True True]''' # In these arrays with a distance of more than 30, the index moved to 30 for the first time value = (np.abs(walks[hits30]) >= 30).argmax(axis=1) value_mean = np.mean(value) print('{}In the group random walk, the index moved to 30 for the first time is:{},Average demand{}Secondary mobility'.format(nwalks,value,np.int(value_mean))) '''15 In the group random walk, the index moved to 30 for the first time is:[813 321 143 269 385 577 771 251 843 911 743],547 moves on average'''
- Draw a graph and count the longest distance
# mean value distance_mean = max_distance.mean() # Greater than mean greater_mean = np.where(max_distance>distance_mean, max_distance, 0) # Less than mean smaller_mean = np.where(max_distance<=distance_mean, max_distance, 0) plt.figure(num=2) plt.title('random walk') x = np.arange(nwalks) # Draw histogram l1 = plt.bar(x, greater_mean, color='r') l2 = plt.bar(x, smaller_mean, color='g') # Drawing data for x0, y0 in zip(x,max_distance): plt.text(x0, y0, '{}'.format(y0), ha='center', va='bottom', fontdict={'size': 8}) # Draw moving average plt.plot(x, np.ones(nwalks)*distance_mean, color='b', linestyle='--') # Draw 30 lines plt.plot(x, np.ones(nwalks)*30, color='y', linestyle='--') # Add notes plt.text(-0.5, distance_mean, 'mean:{:.2f}'.format(distance_mean), ha='right', fontdict={'size': 8}) # Set legend plt.legend(handles=[l1, l2], labels=['greater mean','smaller mean'], loc='best') # Set axis scale format plt.xticks(x) plt.show()
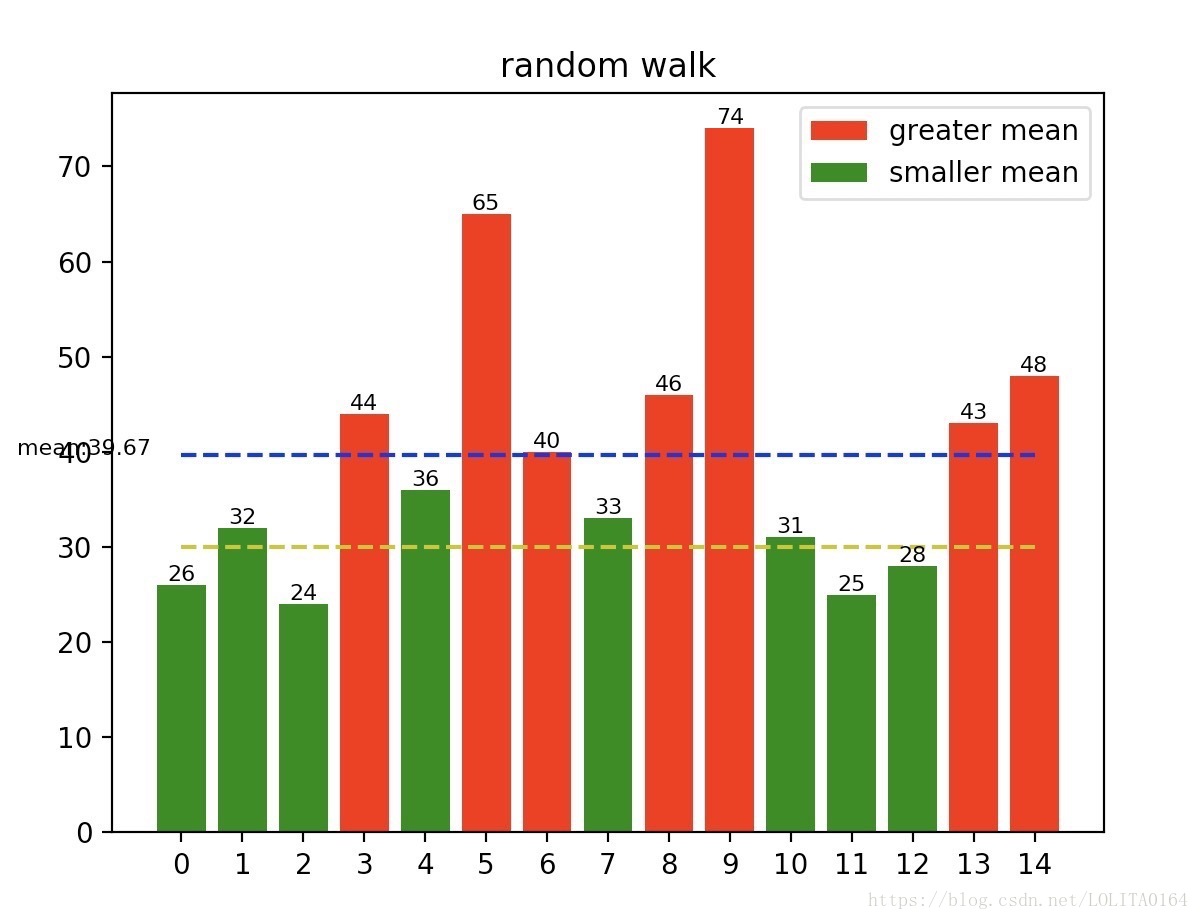
The above is a simple application of random walk. For more data analysis, readers can freely play;
If you want to learn more about the use of matplotlib library, please follow the update later.