The Hanoi Tower problem is a mysterious problem. Today, let's untie its mysterious veil!
First, please look at the question
Title Description
The tower of Hanoi is an ancient mathematical problem:

There are three poles A, B and C. There are n (n > 1) perforated discs on rod A, and the size of the disc decreases from bottom to top. It is required to move all discs to the c-rod according to the following rules:
The requirements are as follows:
① Only one disc can be moved at a time;
② The large plate cannot be stacked on the small plate.
Tip: the disc can be temporarily placed on the BB rod, or the disc removed from the AA rod can be moved back to the A rod, but the above two rules must be followed. Q: how to move it? How many times do you have to move at least?

[problem solving ideas]
There are only two requirements for the Hanoi Tower problem. First, only the top disk can be moved at a time; Second: the plates on the last C pillar should be placed from large to small, not disorderly.
According to common sense, it is easy to think of the handling method of plates. The first step: there are n plates on column A. first, put all n-1 plates on column B in turn, and then put the largest plate on column a directly on column C. finally, just put the plates on column B on column C in turn! This repetitive handling operation can be easily solved by computer. Next, we only need to consider which algorithm to use. So which algorithm should be used? Read the question a little. It is obvious that the question implies that we already know the total number of plates, so we only need to move them all to the destination. Therefore, there will only be fewer and fewer plates on pillar a! The algorithm is ready to come out ---- recursive algorithm, digo!
Next, write the order of transportation directly according to our logic. The code is as follows

#Solve the Hanoi Tower problem by recursive method:
#Step 1: move n-1 plates of column A to column B
#Step 2: move the last plate of column A to column C
#Step 3: move n-1 plates of column B to column C
move_count=0 #Total moves
def hanoi(p1,p2,p3,n):#Number of incoming three columns and plates
    global move_count
    if n==1:#Step 2: if there is only one plate left in column A, move the plate to column C
        print(p1,"->",p3)
        move_count+=1
    else:
        hanoi(p1,p3,p2,n-1)#First, move all n-1 plates of column A to column B
        print(p1,"->",p3)
        hanoi(p2,p1,p3,n-1)#Step 3: move all n-1 plates of column B to column C
        move_count+=1
hanoi("A","B","C",6)
print(move_count)

Through the recursive algorithm, we simply output the transportation process and the total handling times, but this is only the printing of the thinking process, and there is no actual data movement in the space. How to go further and realize the real movement of data? In this way, we need to think about which data structure should be used to store data, and the increase and deletion order of the data structure conforms to the increase and decrease of the plates on the column. Just think a little. The plates put in the column are always taken out first, that is, the plates put in later will be taken out first. By analogy, isn't this the stack? Therefore, directly using the stack to store data can realize the handling of plates! Note: the algorithm still uses recursion. We haven't changed the algorithm
[see code]

#Using the stack data structure to simulate columns to move plates, each column is a stack
#First simulate a stack
class Stack:
   def __init__(self):#Initialization stack
      self.items=[]
   def isEmpty(self):
      if len(self.items)==0:
         print("Stack is empty")
      else:
         print("Stack is not empty")
   def push(self,iteam):
      self.items.append(iteam)
   def pop(self):
      self.items.pop()
   def top(self):
      return self.items[len(self.items)-1]

#Create three stacks to represent the three columns of ABC
a=Stack()
b=Stack()
c=Stack()

#count counts the number of moves
count=0

#Moving plate
def move(p1,p2):
   global count
   value=p1.top()
   p2.push(p1.top())
   p1.pop()
   count += 1
   if p1==a and p2==b:
      print("A->B,The number of plates moved is:",value)
   elif p1==a and p2==c:
      print("A->C,The number of plates moved is:",value)
   elif p1 ==b and p2 ==c:
      print("B->C,The number of plates moved is:", value)
   elif  p1==b and p2==a:
      print("B->A,The number of plates moved is:", value)
   elif  p1==c and p2==a:
      print("C->A,The number of plates moved is:", value)
   elif  p1==c and p2==b:
      print("C->B,The number of plates moved is:", value)
#Add plates to the A-pillar that need to be moved
n=int(input())
for i in range(n):
   a.push(n-i)

def hanoi(p1,p2,p3,n):
   if n==1:
      move(p1,p3)
   else:
      hanoi(p1,p3,p2,n-1)
      move(p1,p3)
      hanoi(p2,p1,p3,n-1)



hanoi(a,b,c,n)
print("The total number of moves is:",count)
a.isEmpty()
b.isEmpty()
c.isEmpty()

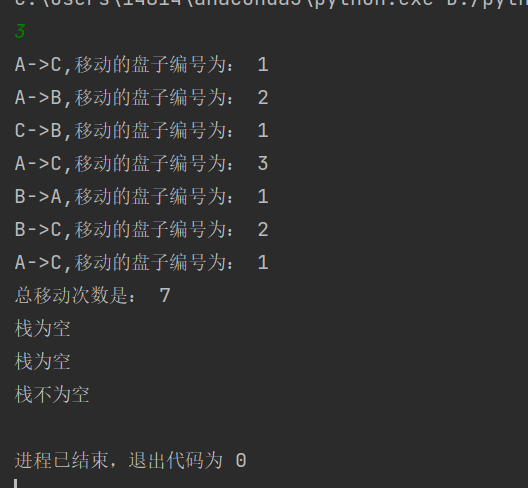
[summary]
With stack storage data to simulate the movement of plates, we can not only know the movement process and times, but also know which plate is moving! Through the final blank judgment, it is obvious that all data in the storage space are moved to the C column. Therefore, it can be seen that the algorithm is the soul and the data structure is the backbone, which cooperate and complement each other.