Portal

Title:

The known sequence A is 1, 11, 111, 1111,... 1, 11, 111, 1111,... 1, 11, 111, 1111,... See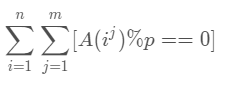

Train of thought:

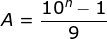Well, then there is the ___________.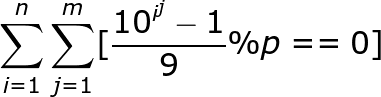

Consider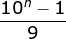In relation to p, first consider the reciprocity of 9 and P

Then it can be changed into ____________.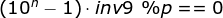

Because of reciprocity inv9_0

So only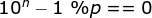

Namely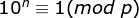

According to Fermat's small theorem, 10 and p are mutually prime.

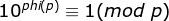
Because 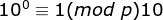Then the cyclic section is at least p_1. Consider whether there are smaller cyclic sections according to the properties of congruences.
                                            

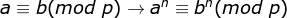
Let d be the factor of p_1, that is, d_p_1, and the smallest cyclic node may be d.
                                                      

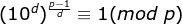
So we can test the factor of p_1 to get the smallest cyclic section D. After finding the smallest cyclic section d, how can we solve the problem? Since the cyclic section is d,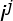It must be a multiple of d. Consider that j is fixed, so long as i contains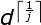That's OK. Let's do that.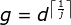So the number of multiples of g in 1 n is . Considering g, we can uniquely decompose d.

Then there will be _____________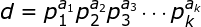

g has.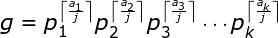

With the change of j, the value of g also changes.When the value of j is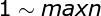When g changes with time, we calculate the contribution of each of them separately as ___________.When J > maxn, g will not change its contribution.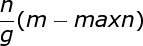

 

 

So the answer can be counted, but when p=2, p=5, 9 and P are mutually prime, but they are ____________.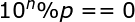So the obvious answer is 0. Second, let's consider the case of p=3. Because p=3 is not mutually exclusive in denominator 9, we can't do that as above. Consider

                                                                                 

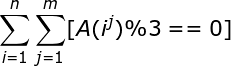
Because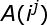For length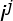If a continuous integer of 1 is divisible by 3, we know that the sum of the digits on each bit of A(i) is S, which is a multiple of 3.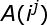The sum of each is the sum of each.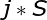j Because every bit on A is 1, so S=i, the final answer is n/3 m.

 

#include <iostream>
#include <cstdio>
#include <cmath>
#include <algorithm>
#include <cstring>
#define ll long long
using namespace std;
ll power(ll a,ll b,ll mod)
{
    ll ans=1;
    while(b)
    {
        if(b&1)
        ans=(ans*a)%mod;
        b>>=1;
        a=(a*a)%mod;
    }
    return ans%mod;
}
ll powerr(ll a,ll b)
{
    ll ans=1;
    while(b)
    {
        if(b&1)
        ans=ans*a;
        b>>=1;
        a=a*a;
    }
    return ans;
}
pair<int,int>a[1005];
int main()
{
    int t;
    cin>>t;
    while(t--)
    {
        ll p,n,m;
        cin>>p>>n>>m;
        if(p==2||p==5)
        {
            cout<<0<<endl;
            continue;
        }
        if(p==3)
        {
            cout<<n/3*m<<endl;
            continue;
        }
        int minn=p-1;
        ll x=minn;
        for(int i=2;i*i<=x;i++)//Looking for the cyclic section of D  
        {
            if(x%i==0)
            {
                if(power(10,i,p)==1)
                minn=min(minn,i);
                if(power(10,x/i,p)==1)
                minn=min(1ll*minn,x/i);
            }
        }
        int cnt=0;
        int maxn=0;
        x=minn;
        for(int i=2;i*i<=x;i++)// Decomposition of D into prime factors 
        {
            if(x%i==0)
            {
                a[cnt].second=0;
                a[cnt].first=i;
                while(x%i==0)
                {
                    a[cnt].second++;
                    x/=i;
                }
                maxn=max(maxn,a[cnt].second);
                cnt++;
            }
        }
        if(x>1)
        {
            a[cnt].first=0;
            a[cnt].second=0;
            a[cnt].first=x;
            a[cnt].second++;
            maxn=max(maxn,a[cnt].second);
            cnt++;
        }
        ll ans=0;
        ll g=1;
        for(int j=1;j<=min(1ll*maxn,m);j++)// Every time the smallest g a[cnt].first/j is found, it is rounded up. 
        {
            g=1;
            for(int i=0;i<cnt;i++)
            {
                ll flag=a[i].second/j;
                if(a[i].second%j)
                flag++;
                g=g*powerr(a[i].first,flag);
            }
            ans=ans+n/g;// There are n/g legitimate i in 1~n 
        }
        if(m>maxn)
        {
            ans=ans+n/g*(m-maxn);// If the value of m is greater than the maximum index, it can be calculated directly. 
        }
        cout<<ans<<endl;
    }
    return 0;
}

Thanks https://blog.csdn.net/ftx456789/article/details/97294635