1. Create a binary tree based on preceding and intermediate traversal
2. Create a binary tree based on sequential and intermediate traversal

Note: It is impossible to restore a binary tree accurately if only one of the three traversals is known.

Preorder and Medium Order Create Binary Trees

For example: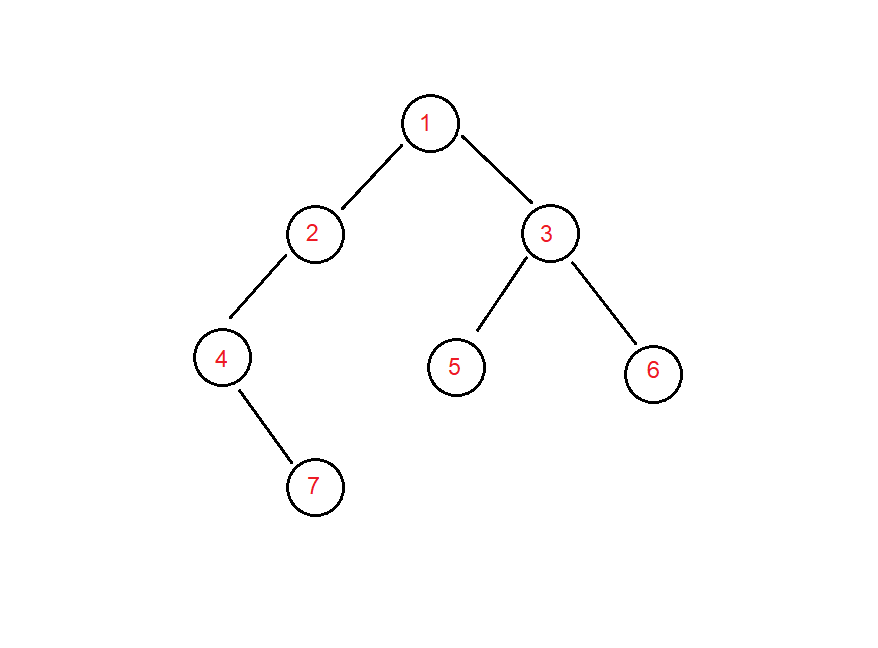

For such a binary tree, the corresponding preceding and middle traversal are:

DataType preorder[] = { 1, 2, 4, 7, 3, 5, 6 };
DataType inorder[] = { 4, 7, 2, 1, 5, 3, 6 };

So how to restore the binary tree?
The first step is to find the root node of the binary tree by traversing in order.
Step 2: Find the root node in the middle order traversal, and separate the left subtree from the right subtree.
Step 3: Think of the left subtree as a binary tree, and then follow these steps, so does the right subtree.

Recursive formula:
If the root node is created, both the left subtree and the right subtree are created. All you need to do is to create the root node.
Root - > left = left subtree; root - > right = right subtree;
Termination conditions:
_size== 0; //size indicates the number of nodes in the binary tree in this lesson, because we pass numbers.
The number of elements in a group of trees to create a binary tree is the number of elements in a group of trees.

The code is as follows:

	typedef int DataType;

	typedef struct BNode
	{
		DataType data;
		struct BNode *left;
		struct BNode *right;
	}BNode;
	
	BNode* CreateNewBNode(DataType data)
	{
		BNode *newBNode = (BNode *)malloc(sizeof(BNode));
		newBNode->data = data;
		newBNode->left = NULL;
		newBNode->right = NULL;
		return newBNode;
	}
	BNode *CreateBinaryTree(DataType preorder[], DataType inorder[], int size)
	{
		//Termination condition
		if (0 == size)
		{
			return NULL;
		}
		DataType rootValue = preorder[0];
		int i = 0;
		//Location of root node in middle order traversal
		for (i = 0; i < size; i++)
		{
			if (inorder[i] == rootValue)
			{
				break;
			}
		}
		//Create the root node
		BNode *root = CreateNewBNode(rootValue);
		//Left tree
		BNode *Tleft = CreateBinaryTree(preorder + 1, inorder, i);
		root->left = Tleft;
		//Right subtree
		BNode *Tright = CreateBinaryTree(preorder + i + 1, inorder + i + 1, size - 1 - i);
		root->right = Tright;
		return root;
	}
	
	void test()
	{
		DataType preorder[] = { 1, 2, 4, 7, 3, 5, 6 };
		DataType inorder[] = { 4, 7, 2, 1, 5, 3, 6 };
		int size = sizeof(preorder) / sizeof(preorder[0]);
		BNode *root = CreateBinaryTree(preorder, inorder, size);
	}

Creating Binary Trees in Postorder and Medium Order

For the above binary tree, the post-order and middle-order traversals are respectively:

	DataType postorder[] = { 7, 4, 2, 5, 6, 3, 1 };
	DataType inorder[] = { 4, 7, 2, 1, 5, 3, 6 };

In fact, the idea of creating binary trees by post-order and mid-order traversal is the same as that of creating binary trees by pre-order and mid-order traversal. The only difference is the recursive function parameters.

The code is as follows:

	BNode *CreateBinaryTree(DataType postorder[], DataType inorder[], int size)
	{
		if (0 == size)
		{
			return NULL;
		}
		DataType rootValue = postorder[size - 1];
		int i = 0;
		for (i = 0; i < size; i++)
		{
			if (inorder[i] == rootValue)
			{
				break;
			}
		}
		BNode *root = CreateNewBNode(rootValue);
		BNode *Tleft = CreateBinaryTree(postorder, inorder, i);
		root->left = Tleft;
		BNode *Tright = CreateBinaryTree(postorder + i, inorder + i + 1, size - 1 - i);
		root->right = Tright;
		return root;
	}
	
	void test1()
	{
		DataType postorder[] = { 7, 4, 2, 5, 6, 3, 1 };
		DataType inorder[] = { 4, 7, 2, 1, 5, 3, 6 };
		int size = sizeof(postorder) / sizeof(postorder[0]);
		BNode *root = CreateBinaryTree(postorder, inorder, size);
	}
	
	int main()
	{
		test1();
		return 0;
	}

In binary tree, we often use recursion. When we use recursion, we often use recursion formulas and termination conditions.
Recursive Formula: If both left and right subtrees are available, there are three nodes in the binary tree that operate downward.
Termination Conditions: Generally, recursive normalization must have termination conditions. Considering termination conditions according to the five basic forms of binary tree is a little simpler.
Finally, we need to consider whether the parameters in the recursive function will change.