stay Summary of basic concepts and terms of trees This paper introduces the basic structure of binary tree.
stay Don't know how to use recursion? Follow the steps! This article introduces how to use recursion.
The structure of binary tree is recursive, so creation and traversal can also be realized by recursion.
Here is a binary tree:
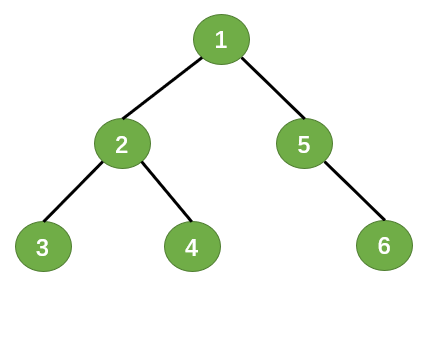
Definition of node:
public class Node { Integer value; Node leftChild; Node rightChild; public Node(Integer value) { this.value = value; } }
establish

The values of each node are saved with an ArrayList set, and a binary tree is created according to the set.
according to Don't know how to use recursion? Follow the steps! The method in analyzes how to recursively create a binary tree.
Step 1: what is the big problem?
Create a binary tree.
private Node createBinaryTree(ArrayList<Integer> inputList) { }
Step 2: what is the simplest question to find? What should I do to satisfy the simplest question?
"Create an empty binary tree" is the simplest problem. When it is satisfied, it returns null directly
private Node createBinaryTree(ArrayList<Integer> inputList) { if (inputList == null || inputList.isEmpty()) {//The simplest question return null; } }
Step 3: what is repetition logic?
Because we put the value of each node in the ArrayList set, we need to take the value from the set for each node of a binary tree.
For each node, it must have left child and right child (the left child and right child of node 3 in the above figure can be regarded as "node with null value"),
Therefore, it is necessary to determine who is the left child and the right child of each node.
So the repetitive logic is:
- Take values from the collection and create nodes.
- Determine the left and right children of the node.
//Big questions private Node createBinaryTree(ArrayList<Integer> inputList) { if (inputList == null || inputList.isEmpty()) {//The simplest question return null; } Node node = null;//Repetitive logic Integer value = inputList.remove(0);//Repetitive logic if (value != null) { node = new Node(value);//Repetitive logic node.leftChild = ?;//Repetitive logic node.rightChild = ?;//Repetitive logic } }
Step 4: call yourself
First, explain the question mark in the last code snippet.
To determine the left child and right child of a node is actually an assignment operation, there must be some optional nodes first.
For example, if we want to determine the left and right children of node 1, then node 2 and node 5 must have been created so that the assignment can be performed.
How to create node 2 and node 5 before assignment? The answer is to call yourself.
We can regard node 2 and node 5 as the root node of another binary tree. As long as we create a binary tree with node 2 or node 5 as the root node, then node 2 and node 5 will be created naturally.
Make sure that the left and right children of node 2 and node 5 are the same. In this way, they will continue to decompose until they are the simplest problems or get null from the collection.
Note: when you call yourself, the parameter decreases through inputList.remove(0) implemented.
//Big questions private Node createBinaryTree(ArrayList<Integer> inputList) { if (inputList == null || inputList.isEmpty()) {//The simplest question return null; } Node node = null;//Repetitive logic Integer value = inputList.remove(0);//Repetitive logic if (value != null) { node = new Node(value);//Repetitive logic node.leftChild = createBinaryTree(inputList);//Repeat the logic and call yourself node.rightChild = createBinaryTree(inputList);//Repeat the logic and call yourself } }
Step 5: Return
It returns the root node, which is determined as the left child or the right child, thus forming a larger binary tree, until the binary tree satisfying the largest problem is successfully created, at this time, the returned root node is the real solution.
//Big questions private Node createBinaryTree(ArrayList<Integer> inputList) { if (inputList == null || inputList.isEmpty()) {//The simplest question return null; } Node node = null;//Repetitive logic Integer value = inputList.remove(0);//Repetitive logic if (value != null) { node = new Node(value);//Repetitive logic node.leftChild = createBinaryTree(inputList);//Repeat the logic and call yourself node.rightChild = createBinaryTree(inputList);//Repeat the logic and call yourself } return node;//return }
ergodic
Preorder traversal
Step 1: what is the big problem?
First, a binary tree is traversed and the values of each node are printed out.
public void preOrderTraveral(Node node) { }
Step 2: what is the simplest question to find? What should I do to satisfy the simplest question?
"Traversing an empty binary tree" is the simplest problem, and no operation is required at this time.
public void preOrderTraveral(Node node) { if (node == null) {//The simplest question return; } }
Step 3: what is repetition logic?
Print the value of each node
public void preOrderTraveral(Node node) { if (node == null) {//The simplest question return; } System.out.print(node.value);//Repetitive logic }
Step 4: call yourself
The process of traversal in advance:
- Traversal root
- Preorder traversal of left subtree
- Preorder traversal right subtree
public void preOrderTraveral(Node node) { if (node == null) {//The simplest question return; } System.out.print(node.value);//Repetitive logic preOrderTraversal(node.leftChild);//Call yourself preOrderTraversal(node.rightChild);//Call yourself }
Parameters pass when calling itself node.leftChild , node.rightChild Keep getting smaller
Step 5: Return
No return value is required.
The same principle of middle order ergodic and post order ergodic
Full code
//Binary tree node public class Node { Integer value; Node leftChild; Node rightChild; public Node(Integer value) { this.value = value; } }
//Binary tree public class BinaryTree { private Node root; public Node getRoot() { return root; } public BinaryTree(ArrayList<Integer> inputList) { Node root = createBinaryTree(inputList); this.root = root; } //Create a binary tree private Node createBinaryTree(ArrayList<Integer> inputList) { if (inputList == null || inputList.isEmpty()) { return null; } Node node = null; Integer value = inputList.remove(0); if (value != null) { node = new Node(value); node.leftChild = createBinaryTree(inputList); node.rightChild = createBinaryTree(inputList); } return node; } //Preorder traversal public void preOrderTraversal(Node node) { if (node == null) { return; } System.out.print(node.value); preOrderTraversal(node.leftChild); preOrderTraversal(node.rightChild); } //Middle order ergodic public void inOrderTraversal(Node node) { if (node == null) { return; } inOrderTraversal(node.leftChild); System.out.print(node.value); inOrderTraversal(node.rightChild); } //Postorder ergodic public void postOrderTraversal(Node node) { if (node == null) { return; } postOrderTraversal(node.leftChild); postOrderTraversal(node.rightChild); System.out.print(node.value); } }
//test public static void main(String[] args) { List<Integer> list = Arrays.asList(new Integer[]{1, 2, 3, null, null, 4, null, null, 5, null, 6}); ArrayList inputList = new ArrayList(list); BinaryTree binaryTree = new BinaryTree(inputList); Node root = binaryTree.getRoot(); System.out.print("Preorder traversal:"); binaryTree.preOrderTraversal(root); System.out.print("\n Middle order traversal:"); binaryTree.inOrderTraversal(root); System.out.print("\n Subsequent traversal:"); binaryTree.postOrderTraversal(root); }
If there is any mistake, please correct it.
The article begins with WeChat official account "pedestrian view".