Catalog
The idea of 0x00A star routing algorithm:
0x01 So how to calculate the speculative cost?
A star routing algorithm is the optimization of Dixtra algorithm.
The idea of 0x00A star routing algorithm:
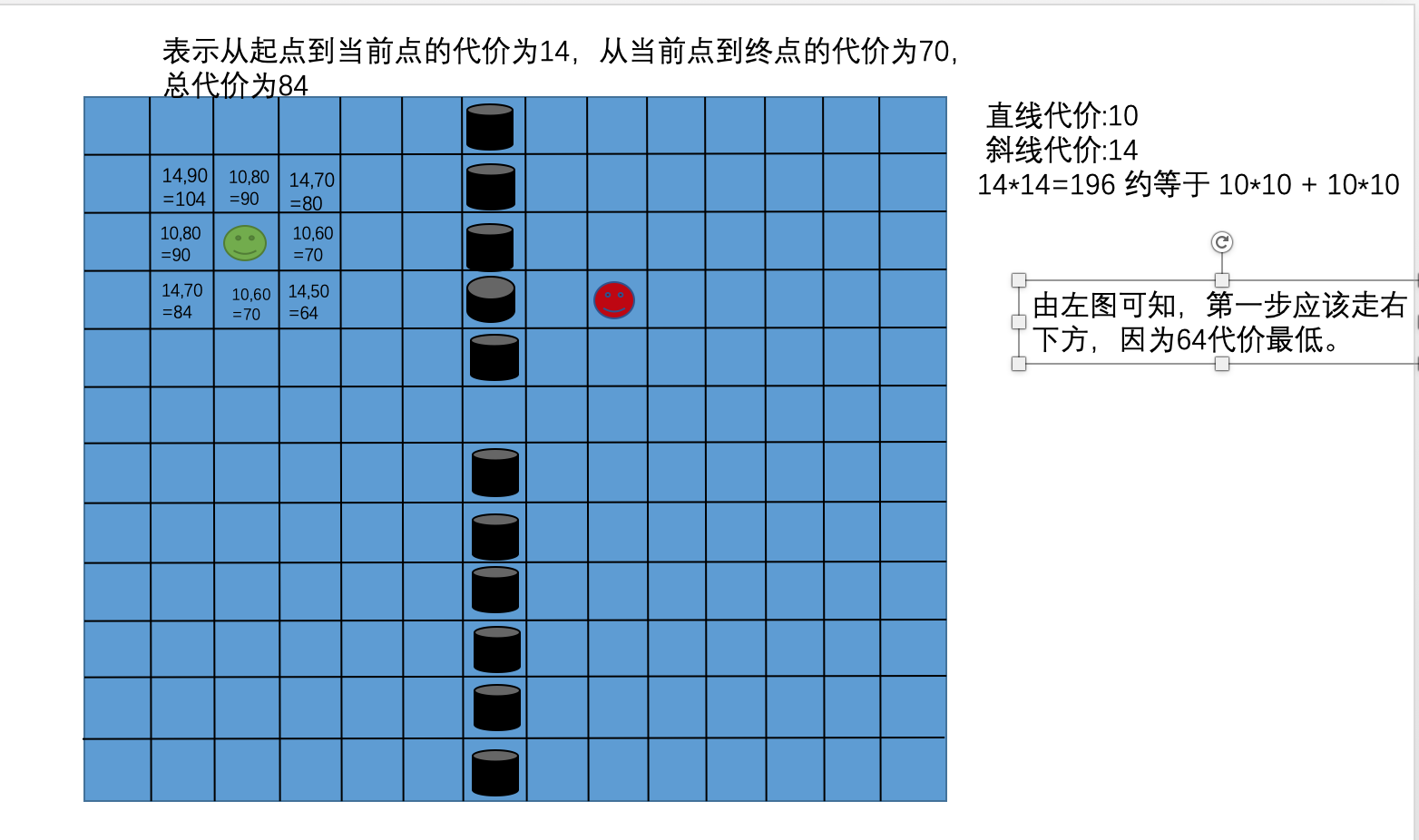
The first step is to calculate the weights (costs) from the starting point to the eight vertices. The weights are not only the actual weights from the starting point to the vertex, but the sum of the actual weights from the starting point to the vertex and the inferred weights from the starting point to the end point. After the calculation is completed, the point with the least weight is selected and marked as the searched point.
The second step is to calculate the weights from the point where the search is completed to each vertex, and select the vertex with the smallest weight, and mark it as the search is completed. By analogy, until the end point is reached.
Summary: Star A routing cycle, constantly calculating which lattice to go next costs the least. Walk on the cheapest grid until you reach the end.
Special attention: the cost from the current point to a lattice = the actual cost + the speculative cost, i.e.
f = g + h + w
f: The cost of the current point to a lattice
g: Actual cost
h: Estimate the cost.
w: Terrain weight. If there are differences between terrain in the process of road-finding, such as uphill and downhill, flat land needs to be added a weight.
0x01 So how to calculate the speculative cost?
Firstly, the estimated cost from the point to the end can be calculated beforehand. If the estimated cost from the point to the end can not be calculated, then the A* routing algorithm can not be used.
Secondly, generally speaking, there are three ways to calculate the presumptive cost:
For example, there are two points A(x1,y1) B(x2,y2) on the plane.
1. Manhattan Distance D = X1 - x2 |+ | Y1 - y2|
2. Chebyshev distance D = max(|x1-x2|,|y1-y2 |)
3. Linear Distance of Euclidean Geometric Plane: D = Calculating the Linear Distance between Two Points by Pythagorean Theorem
Here we use the Manhattan distance and ignore obstacles.
Note: When the distance between the inferred distance and the actual two points is very different, the efficiency of A* routing algorithm may be worse than that of Dixtra algorithm, or even mislead the direction, resulting in the failure to obtain the final solution of the shortest path.
0x02 Code Version 1
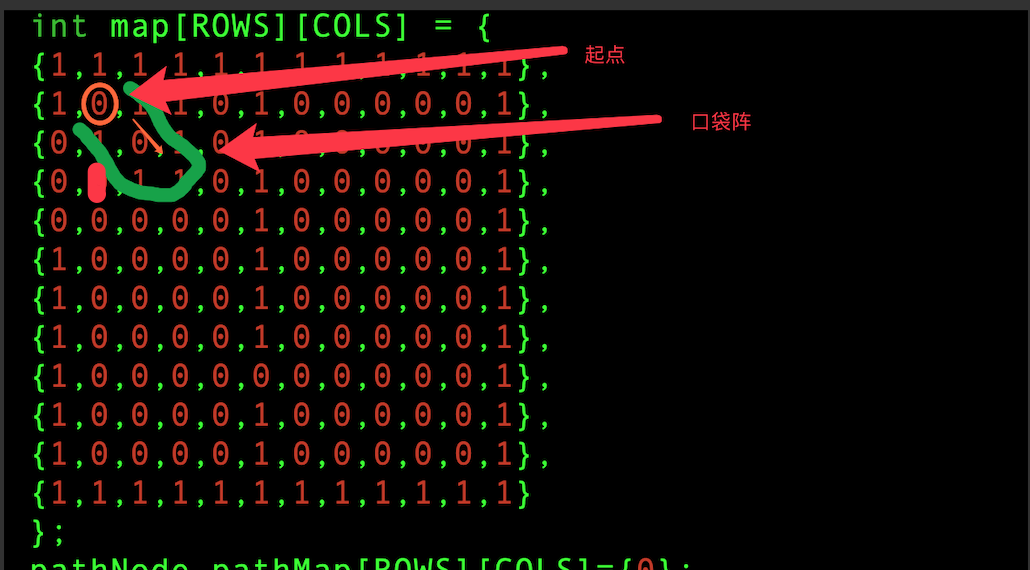
Disadvantage: Can not break through the pocket array, because there is no retreat mechanism
What is a pocket array?
As shown in the figure, the green part is surrounded by a pocket array, because the end point is located at the lower right, so the little man will go down right from the beginning, so that he can reach (2,2) and mark the beginning (1,1) has passed. But (2,2) the eight points around are all walls, so at this time, the villain has no way to go, no way to go back. Get into a dilemma.
How to break through the pocket array? Like the depth routing algorithm, set up a stack, and then step by step? No, actually we can jump back. See Code Version 2 for details.
#include <iostream>
#include <cmath>
#include <unistd.h>
#include <cstdio>
using namespace std;
#define ZXDJ 10//Linear Cost
#define XXDJ 14//slant cost
#define COLS 10
#define ROWS 10
enum dir{p_up,p_down,p_right,p_left,p_rigUp,p_lefUp,p_rigDown,p_lefDown};
struct MyPoint{
int x;
int y;
};
struct weightDirt{
int dirt;
int weight;
};
struct pathNode{
int val;
int isFind;
};
int computeWeight(int direct,MyPoint point,MyPoint endPoint){
int weight = 0;
switch(direct){
case p_up:
case p_down:
case p_right:
case p_left:
weight+=ZXDJ;
break;
case p_rigUp:
case p_lefUp:
case p_rigDown:
case p_lefDown:
weight+=XXDJ;
break;
}
int forecastWeight = abs(point.x - endPoint.x)+abs(point.y - endPoint.y);
forecastWeight *= ZXDJ;
return weight+forecastWeight;
}
void displayPos(int map[COLS][ROWS],MyPoint currentPos){
system("reset");
for(int i=0;i<COLS;i++){
for(int j = 0;j<ROWS;j++){
if(i == currentPos.y && j == currentPos.x){
cout<<"people";
}else{
if(map[i][j] == 1){
cout<<"wall";
}else{
cout<<" ";
}
}
}
cout<<endl;
}
sleep(1);
}
int main(){
int map[COLS][ROWS] = {
{1,1,1,1,1,1,1,1,1,1},
{1,0,0,0,1,1,0,0,0,1},
{1,0,0,0,1,1,0,0,0,1},
{1,0,0,0,1,1,0,0,0,1},
{1,0,0,0,0,0,0,0,0,1},
{1,0,0,0,0,0,0,0,0,1},
{1,0,0,0,1,1,0,0,0,1},
{1,0,0,0,1,1,0,0,0,1},
{1,0,0,0,1,1,0,0,0,1},
{1,1,1,1,1,1,1,1,1,1}
};
pathNode pathMap[COLS][ROWS]={0};
for(int i = 0;i<COLS;i++){
for(int j = 0;j<ROWS;j++){
pathMap[i][j].val = map[i][j];
}
}
MyPoint beginPos = {1,2};
MyPoint endPos = {7,6};
MyPoint tempPos = beginPos;
while(1){
weightDirt minDir ={p_up,10000};
for(int i = 0;i<8;i++){
MyPoint point;
int ret;
switch(i){
case p_up:
point.x = tempPos.x;
point.y = tempPos.y-1;
if(pathMap[point.y][point.x].val == 1 ||pathMap[point.y][point.x].isFind == 1) break;
ret = computeWeight(p_up,point,endPos);
if(ret < minDir.weight){
minDir.dirt = p_up;
minDir.weight = ret;
}
break;
case p_down:
point.x = tempPos.x;
point.y = tempPos.y+1;
if(pathMap[point.y][point.x].val == 1 ||pathMap[point.y][point.x].isFind == 1) break;
ret = computeWeight(p_down,point,endPos);
if(ret < minDir.weight){
minDir.dirt = p_down;
minDir.weight = ret;
}
break;
case p_right:
point.x = tempPos.x+1;
point.y = tempPos.y;
if(pathMap[point.y][point.x].val == 1 ||pathMap[point.y][point.x].isFind == 1) break;
ret = computeWeight(p_right,point,endPos);
if(ret < minDir.weight){
minDir.dirt = p_right;
minDir.weight = ret;
}
break;
case p_left:
point.x = tempPos.x-1;
point.y = tempPos.y;
if(pathMap[point.y][point.x].val == 1 ||pathMap[point.y][point.x].isFind == 1) break;
ret = computeWeight(p_left,point,endPos);
if(ret < minDir.weight){
minDir.dirt = p_left;
minDir.weight = ret;
}
break;
case p_rigUp:
point.x = tempPos.x+1;
point.y = tempPos.y-1;
if(pathMap[point.y][point.x].val == 1 ||pathMap[point.y][point.x].isFind == 1) break;
ret = computeWeight(p_rigUp,point,endPos);
if(ret < minDir.weight){
minDir.dirt = p_rigUp;
minDir.weight = ret;
}
break;
case p_lefUp:
point.x = tempPos.x-1;
point.y = tempPos.y-1;
if(pathMap[point.y][point.x].val == 1 ||pathMap[point.y][point.x].isFind == 1) break;
ret = computeWeight(p_lefUp,point,endPos);
if(ret < minDir.weight){
minDir.dirt = p_lefUp;
minDir.weight = ret;
}
break;
case p_rigDown:
point.x = tempPos.x+1;
point.y = tempPos.y+1;
if(pathMap[point.y][point.x].val == 1 ||pathMap[point.y][point.x].isFind == 1) break;
ret = computeWeight(p_rigDown,point,endPos);
if(ret < minDir.weight){
minDir.dirt = p_rigDown;
minDir.weight = ret;
}
break;
case p_lefDown:
point.x = tempPos.x-1;
point.y = tempPos.y+1;
if(pathMap[point.y][point.x].val == 1 ||pathMap[point.y][point.x].isFind == 1) break;
ret = computeWeight(p_lefDown,point,endPos);
if(ret < minDir.weight){
minDir.dirt = p_lefDown;
minDir.weight = ret;
}
break;
}
}
switch(minDir.dirt){
case p_up:
tempPos.y--;
break;
case p_down:
tempPos.y++;
break;
case p_right:
tempPos.x++;
break;
case p_left:
tempPos.x--;
break;
case p_rigUp:
tempPos.x++;
tempPos.y--;
break;
case p_lefUp:
tempPos.x--;
tempPos.y--;
break;
case p_rigDown:
tempPos.x++;
tempPos.y++;
break;
case p_lefDown:
tempPos.x--;
tempPos.y++;
break;
}
pathMap[tempPos.y][tempPos.x].isFind = 1;
displayPos(map,tempPos);
//printf("current position: (% d,% d) n, tempPos. x, tempPos. y);
if(tempPos.x == endPos.x && tempPos.y == endPos.y){
cout<<"Reach the finish line!"<<endl;
break;
}
}
return 0;
}
0x03 Code Version 2
It can bypass the pocket array.
Ideas: Preparing actual maps, auxiliary maps, node types and coordinate types of auxiliary maps.
Different from each other, write a "chemical tree cycle" to turn the path in the map into the corresponding path tree, and calculate the weight of each location in the process of chemical tree. Then, we save all the current travelable points into a dynamic array (not only the path around the current point, but also the points that we could walk but did not walk before, which is a backoff mechanism), traverse the array to find the point with the lowest weight. Then update the person's location. Continue to cycle until you reach the end point.
How to turn trees into trees? The idea is similar to the breadth routing algorithm: prepare a temporary variable to point out all the points around the current point (eight directions). If the point pointed to satisfies the requirement of the child (is a road and has not passed), then create a corresponding tree node type for the point and add the tree node type to the tree.
#include <iostream>
#include <unistd.h>
using namespace std;
#include <vector>
#define ZXDJ 10
#define XXDJ 10
#define ROWS 12
#define COLS 12
struct MyPoint{
int row;//y
int col;//x
int h;//Presumed weight
int f;//Total weight
int g;//Actual weight
void setF(){
f = g+h;
}
};
struct pathNode{
int val;
bool isFind;
};
enum direct{p_up,p_down,p_left,p_right,lup,ldown,rup,rdown};
struct treeNode{
MyPoint pos;
treeNode* pParent;
vector<treeNode*> child;
};
#if 0
treeNode* CreateNode(const MyPoint& point){
treeNode* pNew = new treeNode;
memset(pNew,0,sizeof(treeNode));
pNew->pos = point;
return pNew;
}
#endif
//Create a tree node and return the node header address
treeNode* CreateNode(const int& row,const int& col){
treeNode* pNew = new treeNode;
memset(pNew,0,sizeof(treeNode));
pNew->pos.row = row;
pNew->pos.col = col;
return pNew;
}
//Judging whether this point can go, can go (the road is not a wall, not through) back to true, can not go back to false.
bool canWalk(pathNode pathMap[ROWS][COLS],MyPoint pos){
//Not within the scope of the map
if(pos.row >= ROWS || pos.row < 0 || pos.col >= COLS || pos.col < 0)
return false;
if(pathMap[pos.row][pos.col].val == 1) return false;
if(pathMap[pos.row][pos.col].isFind == 1)return false;
return true;
}
//Calculate the h value and return, that is, calculate the "speculative weight"
int getH(const MyPoint& currentPos,const MyPoint& endPos){
int x = (currentPos.col>endPos.col)?(currentPos.col - endPos.col):(endPos.col - currentPos.col);
int y = (currentPos.row>endPos.row)?(currentPos.row - endPos.row):(endPos.row - currentPos.row);
return (x+y)*ZXDJ;
}
int main(){
int map[ROWS][COLS] = {
{1,1,1,1,1,1,1,1,1,1,1,1},
{1,0,1,1,0,1,0,0,0,0,0,1},
{0,1,0,1,0,1,0,0,0,0,0,1},
{0,0,1,1,0,1,0,0,0,0,0,1},
{0,0,0,0,0,1,0,0,0,0,0,1},
{1,0,0,0,0,1,0,0,0,0,0,1},
{1,0,0,0,0,1,0,0,0,0,0,1},
{1,0,0,0,0,1,0,0,0,0,0,1},
{1,0,0,0,0,0,0,0,0,0,0,1},
{1,0,0,0,0,1,0,0,0,0,0,1},
{1,0,0,0,0,1,0,0,0,0,0,1},
{1,1,1,1,1,1,1,1,1,1,1,1}
};
pathNode pathMap[ROWS][COLS]={0};
for(int i = 0;i<ROWS;i++){
for(int j = 0;j<COLS;j++){
pathMap[i][j].val = map[i][j];
}
}
MyPoint begPos = {1,1};
MyPoint endPos = {4,9};
//Prepare tree structure
treeNode* pRoot = NULL;
//Starting point becomes root
pRoot = CreateNode(begPos.row,begPos.col);
//Mark the starting point in the auxiliary map
pathMap[begPos.row][begPos.col].isFind = true;
//The temporary pointer points to the current node. This temporary pointer corresponds to a villain.
treeNode* pTemp = pRoot;
//Temporary pointer temporarily saves the children of the current node, but it can also be avoided. It is mainly used to assist the walking point into the tree.
treeNode* pTempChild = NULL;
//Temporary Array: Used to save all the points that can be moved around the current. Then just traverse the array to find the least expensive point.
vector<treeNode*> buff;
//Because you want to traverse the array, you need to prepare two iterators
vector<treeNode*>::iterator it;//Used to switch, that is, to traverse the entire container
vector<treeNode*>::iterator itMin;//To locate the element with the lowest f value in the container
//Temporary Point Type: Used to point out all eight points around a point.
MyPoint tempPos;
bool isFindEnd = false;
//Routing loop
while(1){
for(int i = 0;i<8;i++){
//1. One point presses out eight points.
tempPos = pTemp->pos;
//1.1 Make a temporary exit at each point
switch(i){
case p_up:
tempPos.row--;
tempPos.g += ZXDJ;
break;
case p_down:
tempPos.row++;
tempPos.g += ZXDJ;
break;
case p_right:
tempPos.col++;
tempPos.g += ZXDJ;
break;
case p_left:
tempPos.col--;
tempPos.g += ZXDJ;
break;
case rup:
tempPos.col++;
tempPos.row--;
tempPos.g +=XXDJ;
break;
case rdown:
tempPos.col++;
tempPos.row++;
tempPos.g += XXDJ;
break;
case lup:
tempPos.col--;
tempPos.row--;
tempPos.g += XXDJ;
break;
case ldown:
tempPos.col--;
tempPos.row++;
tempPos.g += XXDJ;
break;
}
//1.2 If this point can go
if(canWalk(pathMap,tempPos)){
//Create tree nodes
pTempChild = CreateNode(tempPos.row,tempPos.col);
//Computing the g-value h-value f-value of a node
pTempChild->pos.g = tempPos.g;
pTempChild->pos.h = getH(pTempChild->pos,endPos);
pTempChild->pos.setF();
//New Node Entering Tree
pTemp->child.push_back(pTempChild);
pTempChild->pParent = pTemp;
//New nodes are saved in arrays
buff.push_back(pTempChild);
//In fact, the last and last buff arrays are retained here. The next place to go.
//This provides a backoff mechanism for dealing with pocket arrays.
//If only the points around the current point are selected at each time, there will be no way to retreat from the pocket array.
printf("(%d,%d) g:%d h:%d f:%d\n",pTempChild->pos.row,pTempChild->pos.col,pTempChild->pos.g,pTempChild->pos.h,pTempChild->pos.f);
//sleep(1);
}
}
//2 traverse the buff array to find the smallest of f
itMin = buff.begin();//Assume that the first element in the array (treeNode * type) corresponds to the smallest element
for(it = buff.begin();it!=buff.end();it++){
itMin =((*itMin)->pos.f > (*it)->pos.f)?it:itMin;
}
//3 The current point (villain) becomes this point
pTemp = *itMin;
//Mark the current point past
pathMap[pTemp->pos.row][pTemp->pos.col].isFind = true;
//Delete this point in the 4 buff array
buff.erase(itMin);
//5. Judging whether to find the end point
if(pTemp->pos.row == endPos.row && pTemp->pos.col == endPos.col){
isFindEnd = true;
break;
}
//6. Judging whether the map has no exit
if(0 == buff.size()) break;//That is to say, if everything in buff is deleted, the map has no exit.
}
//Print path
if(isFindEnd){
printf("Find the end!\n");
while(pTemp){
printf("(%d,%d) ",pTemp->pos.row,pTemp->pos.col);
pTemp = pTemp->pParent;
}
cout<<endl;
}
}