As mentioned earlier Operation and Significance of Image Convolution And some examples are implemented with filter2D function in OpenCV. The filter 2D function in OpenCV only uses a convolution core to deconvolute a single image matrix. In TensorFlow, the convolution operation is mainly used in the convolution layer of CNN, so the input is no longer limited to a three-dimensional or one-dimensional matrix, the number of convolution kernels is no longer single, and the number of channels output is equal to the number of convolution kernels. For this reason, TensorFlow provides a tf.nn.conv2d function to implement a convolution layer. Convolution operation of convolution layer. Definitions are as follows:

def conv2d(input, 
           filter, 
           strides,
           padding, 
           use_cudnn_on_gpu=None,
           data_format=None, 
           name=None)

The parameters are as follows:
The first parameter is the matrix of the current layer, which is a four-dimensional matrix in the convolutional neural network, i.e. [batch,image.size,image.size,depth].
The second parameter is the convolution core (filter), which is created by the tf.get_variable function.
The third parameter is the step size in different dimensions, which corresponds to the first parameter. Although it is also four-dimensional, the number of the first and fourth dimensions must be 1, because we can not choose batch and depth intervally.
The fourth parameter is the boundary filling method.

tf.get_variable function is used to create the weight variable of convolution core and bias. The result is generally used as input of tf.nn.conv2d and tf.nn.bias_add functions. The function is defined as follows:

def get_variable(name,
                 shape=None,
                 dtype=None,
                 initializer=None,
                 regularizer=None,
                 trainable=True,
                 collections=None,
                 caching_device=None,
                 partitioner=None,
                 validate_shape=True,
                 use_resource=None,
                 custom_getter=None)

It should be noted that the second parameter represents the dimension of the convolution core and is also a four-dimensional matrix, [filter.size,filter.size,depth,num]. The first three parameters define the size of a single convolution core, in which depth should be equal to the depth of the layer that needs convolution, that is, the fourth parameter in [batch,image.size,image.size,depth]. Num can be understood as the number of convolution kernels, which determines the number of channels for the next level of output.

So the convolution operation of a convolution layer in CNN can be implemented in TensorFlow with five lines of code - defining the convolution core, defining offset, convolution operation, adding offset, ReLu activation.

filter_weight = tf.get_variable(name,dtype)
biases = tf.get_variable(name,dtype)
conv = tf.nn.conv2d(input, filter_weight,strides,padding)
bias = tf.nn.bias_add(conv, biases)
actived_conv = tf.cnn.relu(bias)

Similarly, TensorFlow provides functions for pooling operations, with the largest pooling being tf.nn.max_pool and the average pooling being tf.nn.avg_pool.

def avg_pool(value, 
            ksize, 
            strides, 
            padding, 
            data_format="NHWC", 
            name=None):

This function is very similar to tf.nn.conv2d. It is not explained by parameters one by one. The main attention must be paid to the second parameter. In tf.nn.conv2d, the second parameter needs training weights. In avg_pool function, only four dimensions need to be given directly. This is because the convolution kernel parameters of pooling operation need not be trained, but are directly specified. What is the maximum pool? It is also related to average pooling. Since pooling operations are generally used to reduce size rather than number of channels, the nuclei of the pooling layer are generally chosen as [1,2,2,1] [1,3,3,1].

For a clearer understanding of convolution and pooling operations, instead of giving the network directly, a specified matrix is operated with a specified convolution core and biased convolution:
Assume that the input matrix is: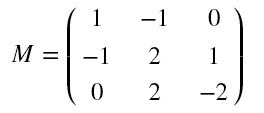

Specify the convolution core as: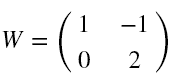

Specifies that the bias is:
[1, 1, 1, ...., 1]

import tensorflow as tf
import numpy as np

M = np.array([
        [[1],[-1],[0]],
        [[-1],[2],[1]],
        [[0],[2],[-2]]
    ])
#Print input matrix shape
print("Matrix shape is: ",M.shape)
#Convolution operation
filter_weight = tf.get_variable('weights',
                                [2, 2, 1, 1], 
                                initializer = tf.constant_initializer([                                                                       [1, -1],                                                                       [0, 2]]))
biases = tf.get_variable('biases', 
                         [1],
                         initializer = tf.constant_initializer(1))
#Adjust the format of the input matrix to meet the requirements of TensorFlow, batch=1
M = np.asarray(M, dtype='float32')
M = M.reshape(1, 3, 3, 1)

x = tf.placeholder('float32', [1, None, None, 1])
conv = tf.nn.conv2d(x, filter_weight, strides = [1, 2, 2, 1], padding = 'SAME')
bias = tf.nn.bias_add(conv, biases)
pool = tf.nn.avg_pool(x, ksize=[1, 2, 2, 1], strides=[1, 2, 2, 1], padding='SAME')
with tf.Session() as sess:
    tf.global_variables_initializer().run()
    #Feed M to a defined operation
    convoluted_M = sess.run(bias,feed_dict={x:M})
    pooled_M = sess.run(pool,feed_dict={x:M})

    print("convoluted_M: \n", convoluted_M)
    print("pooled_M: \n", pooled_M)

Result:
Matrix shape is: (3, 3, 1)
convoluted_M:
[[[[ 7.]
[ 1.]]

[[-1.]
[-1.]]]]
pooled_M:
[[[[ 0.25]
[ 0.5 ]]

[[ 1. ]
[-2. ]]]]

The results in IPython are shown above, and for convenience, they are in the form of normal matrices:
convoluted_M:
[[
[[ 7.] [ 1.]]
[[-1.] [-1.]]
]]
pooled_M:
[[
[[ 0.25] [ 0.5 ]]
[[ 1. ] [-2. ]]
]]
This is the case above. It should be noted that the boundary filling is unilateral filling (zero filling) on the right and bottom, that is:

(3-2+1)/2+1=2

After convolution, adding bias is convoluted_M, and after average pooled_M.