Today, the arithmetic teacher set up a divide-and-conquer job to build graycodes. As a programming whitespace, he thought about it for hours before he happened to finish it. So he thought about taking his own notes on CSDN, which is also my first blog post.
Origin:
Gray code is a 2^n sequence with no identical elements in the sequence, and each element is a binary bit string of length n, and only one adjacent element is different....... Design a divide and conquer algorithm to construct a corresponding gray code for any n value.
First of all, we need to know what Gray Code is. Actually, I didn't understand it at first. I checked the data about it. It looks like this in the following figure.
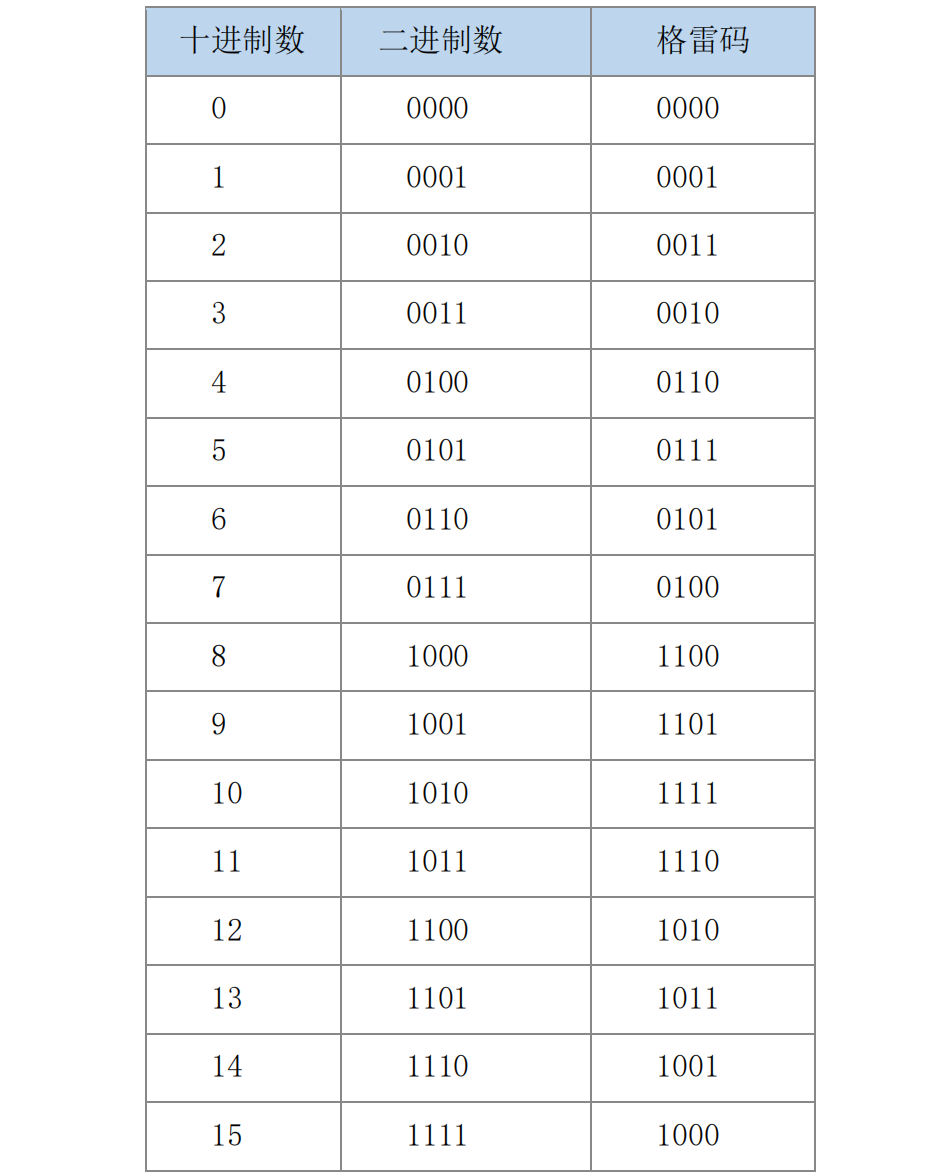 Graph Source From
Binary to Gray Code Conversion_Patient Little Black's Blog-CSDN Blog_Binary to Gray Code Conversion
Graph Source From
Binary to Gray Code Conversion_Patient Little Black's Blog-CSDN Blog_Binary to Gray Code Conversion
If interested students can get a better understanding, they can continue to look at it if they just do (ying) fu.
Then there is the Divide and Cure template taught by the algorithm teacher:
/*
* Parameter description:
* arr[] Processing Arrays
* left Array Processing Lower Limit
* right Array processing upper limit
*/
void Function(arr[], int left, int right){
if(/*Satisfies the condition*/){
//Recursive Exit
}else{
//Calculate Intermediate Value
center = (left + right)/2;
Function(arr, left, center);
Function(arr, center+1, right);
}
}For ease of operation, I've just shown it with a gray code of n 3, because I've only finished the function according to the distribution rule to complete the job.
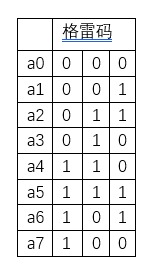 Probably not finding the rule
Probably not finding the rule
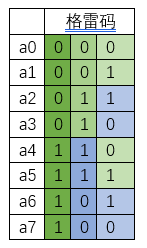 It looks much better then
It looks much better then
You can see that a column labeled in green follows the rule of "0 before 1". Blue is the opposite. According to the idea of divide and conquer, we can first process the numbers in the first column, that is, assign 0 to the first half of the array and 1 to the second half. Then use recursion to pass in the subscript of the first half as a parameter, for example, a0-a4 is "0 before 1" in the first recursion.Then continue to modify according to the rules, of course, the data in the last modification needs to be moved one bit to the left, that is, multiply the original value by 10. The code is as follows:
void toGeleiCode(int arr[], int left, int right) {
//Exit recursion when left==right
if (left == right)
{
return;
}
else
{
//Calculate Intermediate Value
int center = (left + right) / 2;
//First Half Array Right Shift and Increment
for (int i = left; i <= center; i++)
{
arr[i] = arr[i] * 10 + 0;
}
//Move the latter half of the array right and increment
for (int i = center+1; i <= right; i++)
{
arr[i] = arr[i] * 10 + 1;
}
//Divide the array into two parts and recursively continue to gray the next one
toGeleiCode(arr, left, center);
toGeleiCode(arr, center + 1, right);
}
}
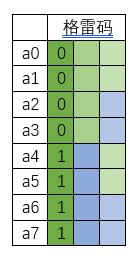 First Execution Function
First Execution Function
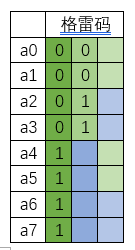 First recursion
First recursion
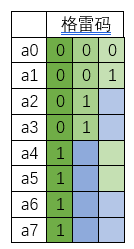 Second recursion
Second recursion
It's almost enough to write here, but careful students will surely find that there will also be a "1 then 0" section so that they can't continue to modify it through the rules above.
But is it completely different? Obviously it's just the increments that are different. Then we need to introduce new variables to judge and save the increments. We can see that the latter half of an array of recursive functions is the rule of "one after zero" each time.
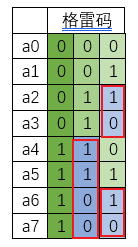
Then all we need to do is to reference a parameter to tell our function what value this parameter is, to execute the rule of "0 before 1", and to execute the rule of "1 after 0" for other values. For convenience, we use the bool variable here, and also save the increments of the first and second half arrays as variables.
void toGeleiCode(int arr[], int left, int right, bool flag = true) {
//Exit recursion when left==right
if (left == right)
{
return;
}
else
{
//Set the increment after the number is moved right in the array
/*
* flag True
* Add 0 to the first half and 1 to the second half.
* flag False
* Add 1 to the first half and 0 to the second half.
*/
int left_add = flag ? 0 : 1;
int right_add = flag ? 1 : 0;
//Calculate Intermediate Value
int center = (left + right) / 2;
//First Half Array Right Shift and Increment
for (int i = left; i <= center; i++)
{
arr[i] = arr[i] * 10 + left_add;
}
//Move the latter half of the array right and increment
for (int i = center+1; i <= right; i++)
{
arr[i] = arr[i] * 10 + right_add;
}
//Divide the array into two parts and recursively continue to gray the next one
/*
* The next bit of the first half of the array is 0 followed by 1, that is, flag is ture
* The next bit of the latter half array matches first 1 then 0, that is, flag is false
*/
toGeleiCode(arr, left, center, true);
toGeleiCode(arr, center + 1, right, false);
}
}Execution effect:

Finally, complete code is attached (function is streamlined):
#include "iostream"
#include "iomanip"
using namespace std;
int main() {
void toGeleiCode(int arr[], int left, int right, bool flag = true);
int n;
cout << "Please enter n Value:";
cin >> n;
//Set array upper and lower bounds
int left = 0;
int right = (1 << n)-1;
//Define dynamic arrays
int* arr = new int[right+1];
//Initialize Array
for (int i = 0; i <= right; i++)
arr[i] = 0;
//Execute Function
toGeleiCode(arr, left, right);
//Output Grayscale Array
cout << "The Gray array is as follows" << endl;
for (int i = 0; i <= right; i++)
{
cout << setw(n) << setfill('0') << arr[i] << endl;
}
return 0;
}
void toGeleiCode(int arr[], int left, int right, bool flag = true) {
//Exit recursion when left==right
if (left == right)
{
return;
}
else
{
//Set the increment after the number is moved right in the array
/*
* flag True
* Add 0 to the first half and 1 to the second half.
* flag False
* Add 1 to the first half and 0 to the second half.
*/
//int left_add = flag ? 0 : 1;
//int right_add = flag ? 1 : 0;
//Calculate Intermediate Value
int center = (left + right) / 2;
//First Half Array Right Shift and Increment
for (int i = left; i <= center; i++)
{
arr[i] = arr[i] * 10 + (int)!flag;
}
//Move the latter half of the array right and increment
for (int i = center+1; i <= right; i++)
{
arr[i] = arr[i] * 10 + (int)flag;
}
//Divide the array into two parts and recursively continue to gray the next one
/*
* The next bit of the first half of the array is 0 followed by 1, that is, flag is ture
* The next bit of the latter half array matches first 1 then 0, that is, flag is false
*/
toGeleiCode(arr, left, center, true);
toGeleiCode(arr, center + 1, right, false);
}
}Finally, there may be some typesetting problems or errors in the first writing. You are welcome to point out rationally.
I am 61, a little white person who does not know programming.