What is an expression two fork tree?
The expression binary tree is composed of numbers and operators. The operators are the parent nodes and the numbers are the left and right nodes. As shown in the following figure: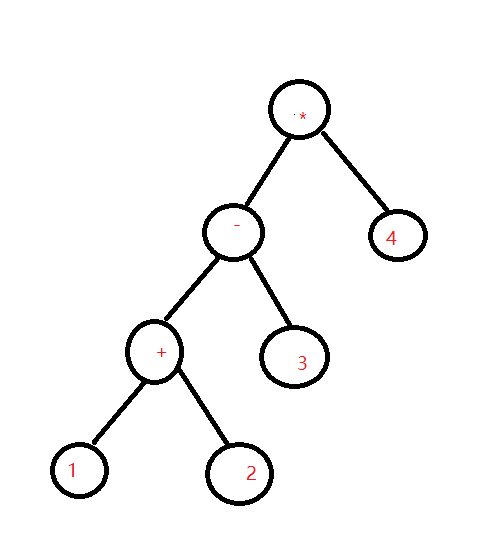

How to build a tree?

1. Create an array queue number_list and operation_list, and store numbers and operators in the array queue, respectively.
2. Two numbers are extracted from number_list, and an operator is extracted from operation_list to form a node. And delete the corresponding numbers and nodes.
3. Repeat the second step until there is only one node left in the numeric list, which is the root node.

Three methods of traversing binary trees

(The following traversal results are illustrated by the binary tree of the above graph expression)

1. Priority arrangement:
   The traversal order is: root node - > left node - > right node.
   Ergodic results: **-+1234*
2. In order:
   The traversal order is: left node - - - - > root node - - - - > right node.
   Ergodic results: 1 + 2-34*
3. Post-order arrangement:
   The traversal order is: left node - - - - > right node - - - - > root node.
   Ergodic results: 12 + 3-4*

Code example

Node class:

Attributes: left node, right node, data

public class Node{
	
	Node left,right;
	char data;
	
	public Node(){}
	
	public Node(char data){
		this.data = data;
	}
	
	
	public char getData(){
		return data;
	}
	
	public void setLeft(Node left){
		this.left = left;
	}
	
	public Node getLeft(){
		return left;
	}
	
	public void setRight(Node right){
		this.right = right;
	}
	
	public Node getRight(){
		return right;
	}

}

Binary Trees:

public class Tree {
	
	static Node root;	//Root node
	String str;
	
	public void build_tree(String str){
		//Create linked lists to store operators
		ArrayList<Node> operation = new ArrayList<>();
		//Create linked lists to store numbers
		ArrayList<Node> number = new ArrayList<>();
		//Store operators and numbers in respective array queues
		for(int i=0;i<str.length();i++){
			char ch = str.charAt(i);
			Node temp = new Node(ch);
			if(ch>='0' && ch<='9'){
				number.add(temp);
			}else {
				operation.add(temp);
			}
		}
		//Constructing Binary Tree
		while(operation.size()>0){
			//Take the first element in the array queue (number) as the left node
			Node left = number.get(0);
			//Remove the first element from (number)
			number.remove(0);
			//Take the first element in the array queue (number) as the right node
			Node right = number.get(0);
			//Remove the first element from (number)
			number.remove(0);
			//Remove the first element from the array queue
			Node root = operation.get(0);
			//Remove the first element from the operation
			operation.remove(0);
			//Operators are used as root nodes, while left and right nodes are used as left and right nodes, respectively.
			root.setLeft(left);
			root.setRight(right);
			//Take the newly generated node as the first node
			number.add(0, root);
		}
		root = number.get(0);
	}
	
	//Preorder traversal (around the root)
	public void before_output(Node node){
		if(node==null){
			return ;
		}else {
			System.out.print(node.data);
			before_output(node.getLeft());
			before_output(node.getRight());
		}
	}
	
	//Ordered traversal (left root right)
	public void middle_output(Node node){
		if(node.getLeft()!=null){
			middle_output(node.getLeft());
		}
		System.out.print(node.data);
		if(node.getRight()!=null){
			middle_output(node.getRight());
		}
	}
	
	//Post-order traversal (left and right roots)
	public void behind_output(Node node){
		if(node.getLeft()!=null){
			behind_output(node.getLeft());
		}
		if(node.getRight()!=null){
			behind_output(node.getRight());
		}
		System.out.print(node.data);
	}
	
	
	public static void main(String[] args){
		Tree tree = new Tree();
		tree.build_tree("1+2-3*4/5");
		System.out.println("Priority Arrangement: Roots->Left->Right:");
		tree.before_output(root);
		System.out.println();
		System.out.println("Middle order: left->right->root:");
		tree.middle_output(root);
		System.out.println();
		System.out.println("Postordinal Arrangement: Left->right->Root:");
		tree.behind_output(root);
	}
	
}

sample output

Priority: root - > left - > right:
/*-+12345
 Middle order: left - > root - > right:
1+2-3*4/5
 Postordinal arrangement: left - > right - > root:
12+3-4*5/

Can undertake various projects, interested parties add QQ: 1217898975