Jaccard Index (IoU, degree of overlap)
Jaccard Index (Jaccard coefficient), or Jaccard Overlap (Jaccard Overlap) or intersection over Union (IoU), measures the degree of overlap between the two frames. This index can reflect the proximity between the prediction frame and the real frame, which will be used in calculating loss and NMS (non maximum suppression). As shown in the figure below.
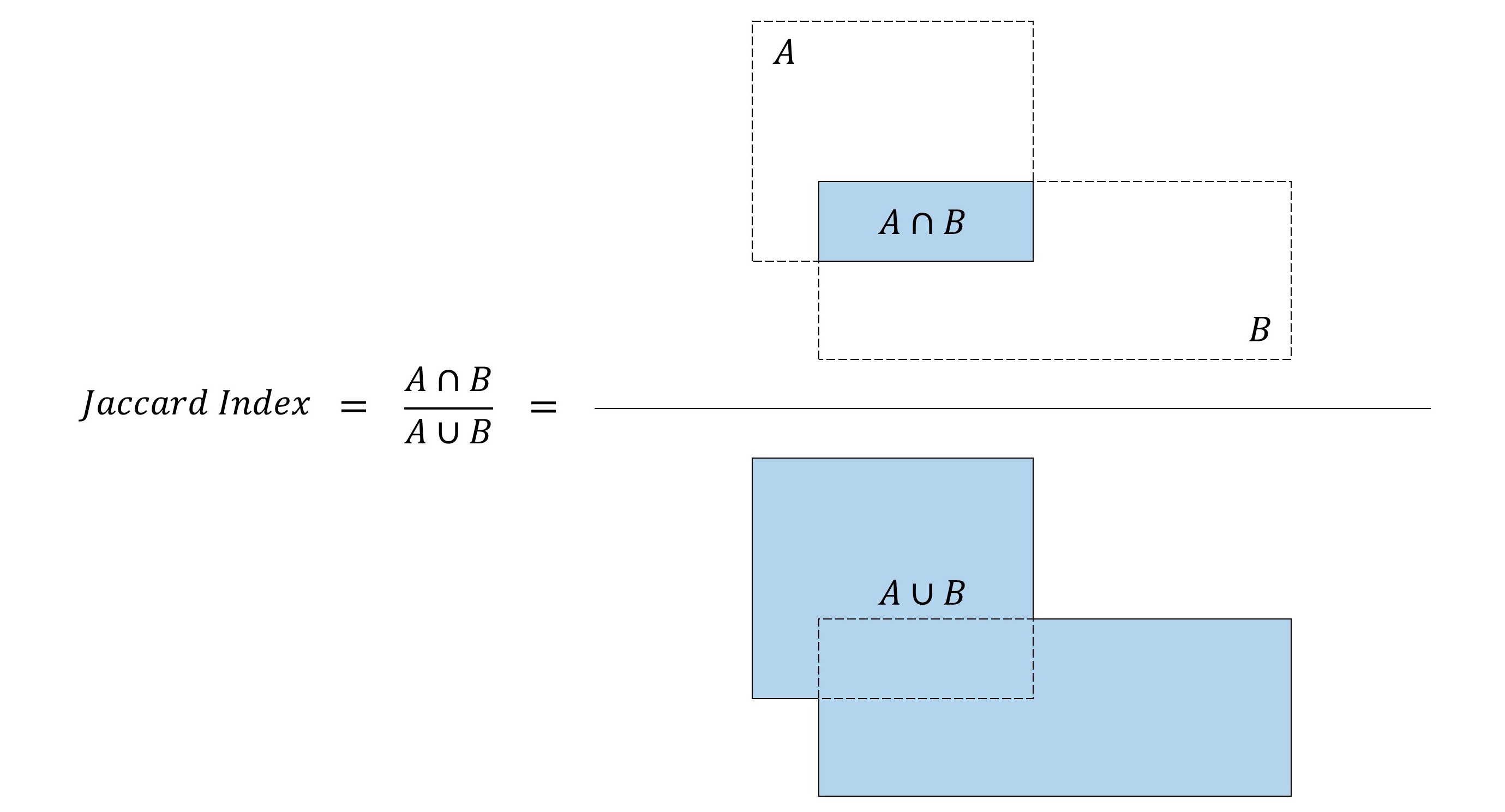
obviously, the value of Jaccard coefficient is
[
0
,
1
]
[0, 1]
Between [0,1], when the value is 0, it indicates that the intersection of the two boxes is 0, that is, the two boxes do not overlap; When the value is 1, the intersection and union of the two boxes are the same, that is, the two boxes completely overlap.
the code implementation of Jaccard coefficient may not be well understood. We need to find two quantities, one is the intersection area, the other is the Union area, and
and
collection
noodles
product
=
frame
A
of
noodles
product
+
frame
B
of
noodles
product
−
hand over
collection
noodles
product
Union area = area of box A + area of Box B - intersection area
Union area = area of box A + area of Box B − intersection area. The areas of box A and Box B are very easy to calculate, so we focus on the calculation of intersection area. Consider some common intersection methods, as shown in the figure below. Green points represent the upper left corner of the intersection area and blue points represent the lower right corner of the intersection area.
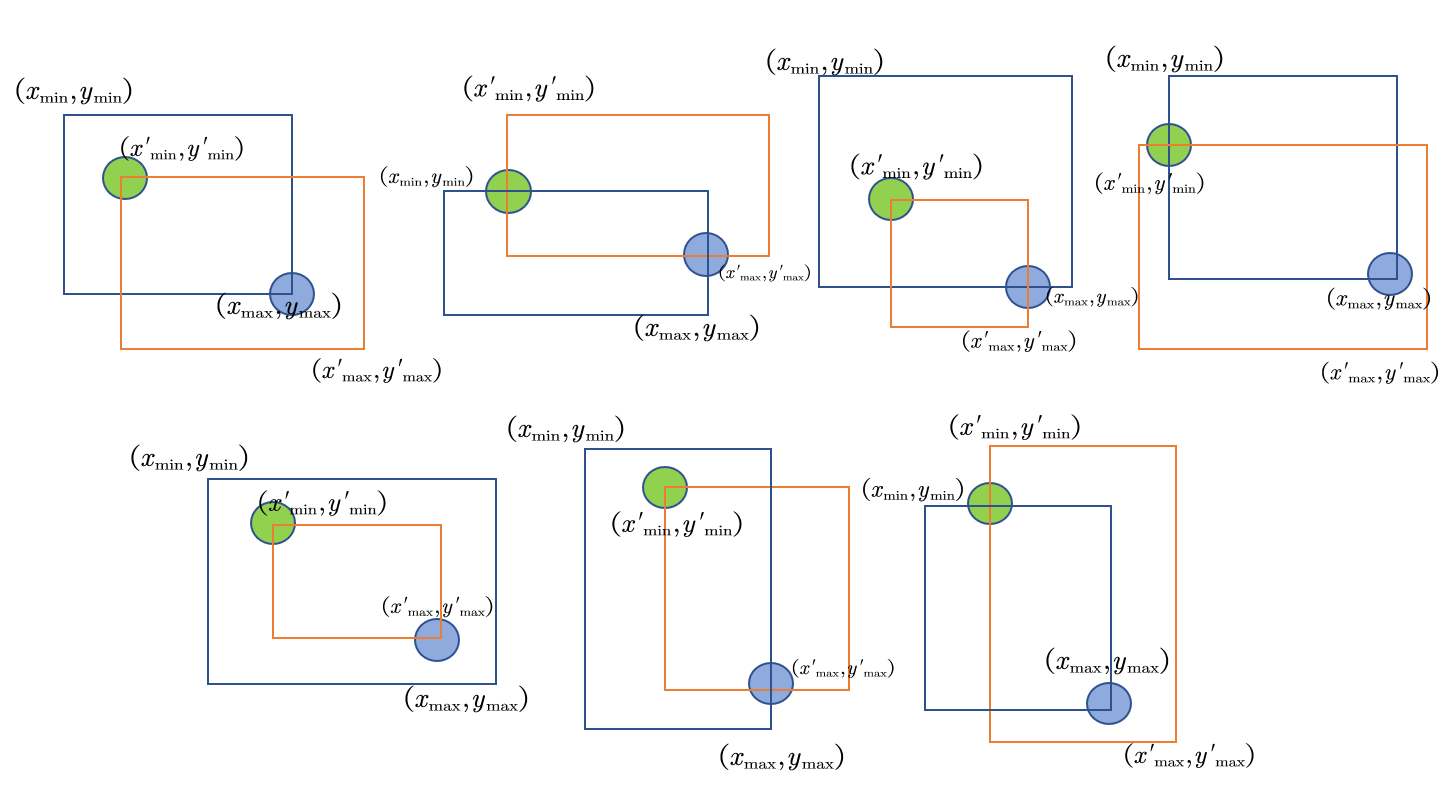
from the above figure, we can see that the intersection area can be represented by two points, which is the boundary coordinates of the intersection area, and the boundary coordinates of the whole intersection area can be expressed as:
(
I
x
min
,
I
y
min
,
I
x
max
,
I
y
max
)
(I_{x_{\min}}, I_{y_{\min}}, I_{x_{\max}}, I_{y_{\max}})
(Ixmin,Iymin,Ixmax,Iymax)
his
in
:
I
x
min
=
max
{
x
min
,
x
min
′
}
,
I
y
min
=
max
{
y
min
,
y
min
′
}
,
I
x
max
=
min
{
x
max
,
x
max
′
}
,
I
y
max
=
min
{
y
max
,
y
max
′
}
Including: I_{x_{\min}} =\max\{x_{\min}, x^{\prime}_{\min}\}, \quad I_{y_{\min}} =\max\{y_{\min}, y^{\prime}_{\min}\}, \ I_{x_{\max}} =\min\{x_{\max}, x^{\prime}_{\max}\}, \quad I_{y_{\max}} =\min\{y_{\max}, y^{\prime}_{\max}\}
Where: Ixmin = max{xmin, xmin '}, Iymin = max{ymin, ymin'}, Ixmax = min{xmax, xmax '}, Iymax = min{ymax, ymax'}
Therefore, the intersection area can be obtained as
S
=
(
I
y
max
−
I
y
min
)
(
I
x
max
−
I
x
min
)
S = (I_{y_{\max}} - I_{y_{\min}})(I_{x_{\max}} - I_{x_{\min}})
S=(Iymax−Iymin)(Ixmax−Ixmin).
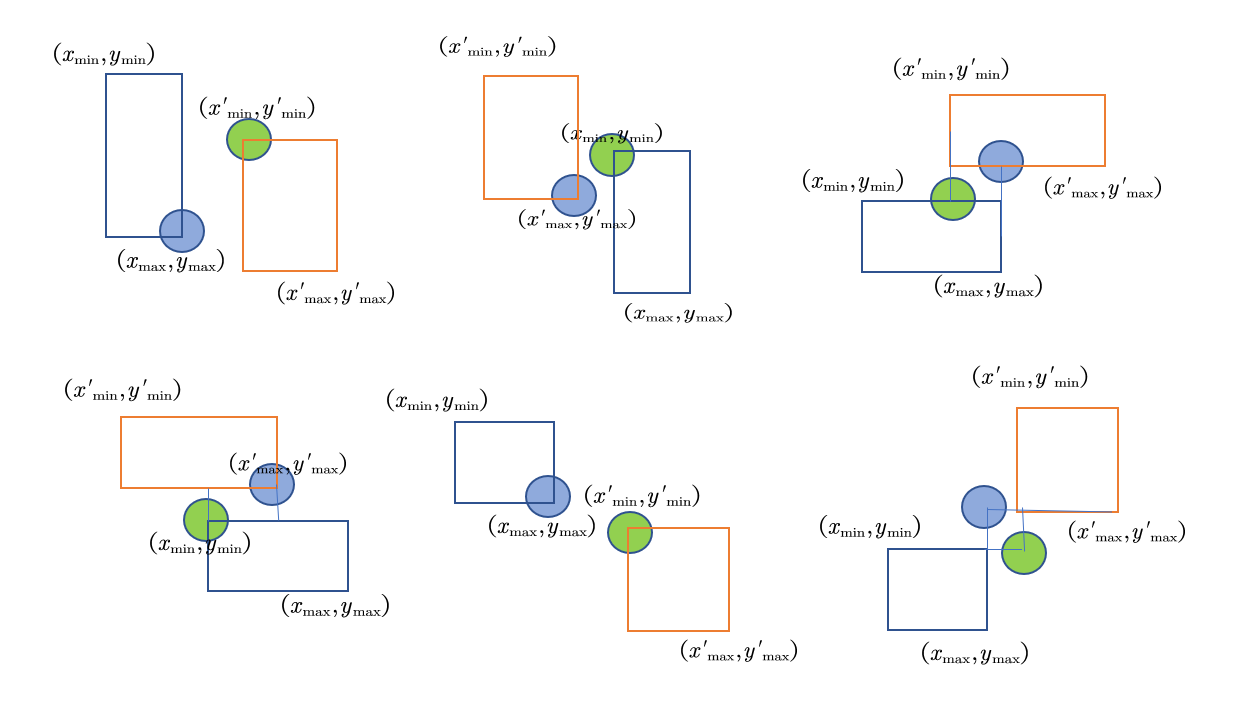
however, when the two boxes do not coincide, what will this formula calculate? Considering the non coincidence, as shown in the figure below, the green dot represents the "upper left corner" calculated by the above formula, and the blue dot represents the "lower right corner" calculated by the above formula:
at this time, we consider the above area formula:
S
=
(
I
y
max
−
I
y
min
)
(
I
x
max
−
I
x
min
)
S = (I_{y_{\max}} - I_{y_{\min}})(I_{x_{\max}} - I_{x_{\min}})
S=(Iymax − Iymin) (Ixmax − Ixmin), either
I
y
max
−
I
y
min
<
0
I_{y_{\max}} - I_{y_{\min}} < 0
Iymax − Iymin < 0, or
I
x
max
−
I
x
min
<
0
I_{x_{\max}} - I_{x_{\min}} < 0
Ixmax − Ixmin < 0, or both are less than 0, so we can calculate the intersection area in this way: once the two formulas are less than 0, we set it to 0, so 0 multiplied by any number is 0, so the intersection area calculation result is 0, otherwise we can use the above formula to obtain the intersection area.
to sum up, we can get the following code for finding intersection:
def find_intersection(set_1, set_2):
"""
Calculate the intersection area of each box in the first set and each box in the second set
:param set_1: One shape by[m,4]of tensor,representative m Boundary coordinates
:param set_2: One shape by[n,4]of tensor,representative n Boundary coordinates
:return: One shape by[m,n]of tensor,For example:[0,:]express set_1 Box 1 and set_2 Intersection area of each box in
"""
# The shapes of the two tensors in the max function are [m,1,2], [1,n,2], and the broadcast mechanism can be applied. Finally, the shape of the tensor is [m,n,2]
# For example: [0,:, 2] indicates set_ The first box in 1 and set_ Coordinates of the upper left corner of the intersection of all frames in 2
lower_bounds = torch.max(set_1[:, :2].unsqueeze(1), set_2[:, :2].unsqueeze(0)) # [m, n, 2]
# Calculate the coordinates of the lower right corner
upper_bounds = torch.min(set_1[:, 2:].unsqueeze(1), set_2[:, 2:].unsqueeze(0)) # [m, n, 2]
# Set two subtractions less than 0 to 0
intersection_dims = torch.clamp(upper_bounds - lower_bounds, min=0) # [m, n, 2]
# Multiply to get the intersection area
return intersection_dims[:, :, 0] * intersection_dims[:, :, 1] # [m, n]
utilization and collection noodles product = frame A of noodles product + frame B of noodles product − hand over collection noodles product Union area = area of box A + area of Box B - intersection area Union area = area of box A + area of Box B − intersection area, and then the code for calculating Jaccard coefficient is obtained:
def find_jaccard_overlap(set_1, set_2):
"""
Calculates the distance between each box in the first set and each box in the second set Jaccard coefficient
:param set_1: One shape by[m,4]of tensor,representative m Boundary coordinates
:param set_2: One shape by[n,4]of tensor,representative n Boundary coordinates
:return: One shape by[m,n]of tensor,For example:[0,:]express set_1 Box 1 and set_2 Of each box in the Jaccard coefficient
"""
# The intersection of each box with other boxes
intersection = find_intersection(set_1, set_2) # [m, n]
# Calculate the area of each box in each set
areas_set_1 = (set_1[:, 2] - set_1[:, 0]) * (set_1[:, 3] - set_1[:, 1]) # [m]
areas_set_2 = (set_2[:, 2] - set_2[:, 0]) * (set_2[:, 3] - set_2[:, 1]) # [n]
# Total area minus intersection is union
# The function of unsqueeze is also to meet the conditions of broadcasting mechanism
union = areas_set_1.unsqueeze(1) + areas_set_2.unsqueeze(0) - intersection # [m, n]
# Jaccard coefficient = intersection area / Union area
return intersection / union # [m, n]