
preface:
It seems that we did talk about heap in C language teaching before, but it is the heap in the operating system. The heap we are going to talk about today is the heap in the data structure. There are also stacks and heaps in the data structure, which has nothing to do with the stack and heap in the memory division of the operating system. I couldn't move anyone else, so I planned to write another 100 million blogs.
 (Zhou Shuren is old as soon as he speaks)
(Zhou Shuren is old as soon as he speaks)
1, Concept and properties of heap
0x00 concept of heap
[Baidu Encyclopedia] heap is a general term for a special kind of data structure in computer science. Heap is usually an array object that can be regarded as a complete binary tree.
📚 If there is a set of keys  , Piles are divided into large piles and small piles. Store all its elements in an array in the order of a complete binary tree:
, Piles are divided into large piles and small piles. Store all its elements in an array in the order of a complete binary tree:
① If satisfied 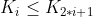 And
And 
 Is called a small pile.
Is called a small pile.
② If satisfied  And
And 
 , Is called a pile.
, Is called a pile.
We call the heap with the largest root node the maximum heap (i.e. large root heap), and the heap with the smallest root node the minimum heap (i.e. small root heap).
🔺 in summary:
① Pile: in any tree and subtree in the tree, the value of the father is greater than or equal to that of the child(  )
)
② Small pile: in any tree and subtree in the tree, the value of the father is less than or equal to that of the child ( 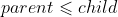 )
)
0x01 nature of heap
① Heap is always a complete binary tree.
② The value of a node in the heap is always not greater than or less than the value of its parent node.

0x02 role of reactor
① Heap sort
② Settle  Problem, in
Problem, in  Find the largest number of front
Find the largest number of front  One or find the smallest
One or find the smallest  individual
individual
......
2, Definition of heap
All arrays can be represented as a complete binary tree, but it is not necessarily a heap. Heap: all fathers in the tree are greater than or equal to children. Small heap: all fathers in the tree are less than or equal to children. Next, we will implement a heap.
0x00 array heap
typedef int HPDataType;
typedef struct Heap {
HPDataType* array; //Point to a dynamic array
int size; //Number of valid data
int capacity; //Size of capacity space
} HP;0x01 interface function
📚 Several interface functions need to be implemented:
/* Heap initialization */
void HeapInit(HP* php);
/* Heap destruction */
void HeapDestroy(HP* php);
/* Heap printing */
void HeapPrint(HP* php);
/* Determine whether the heap is empty */
bool HeapIfEmpty(HP* hp);
/* Heap insertion */
void HeapPush(HP* php, HPDataType x);
/* Check capacity */
void HeapCheckCapacity(HP* php);
/* Exchange function */
void Swap(HPDataType* px, HPDataType* py);
/* Large root pile up regulation */
void BigAdjustUp(int* arr, int child);
/* Small root pile up regulation */
void SmallAdjustUp(int* arr, int child);
/* Deletion of heap */
void HeapPop(HP* php);
/* Small root pile down regulation*/
void SmallAdjustDown(int* arr, int n, int parent);
/* Large root pile down regulation */
void BigAdjustDown(int* arr, int n, int parent);
/* Return heap top data*/
HPDataType HeapTop(HP* php);
/* Count the number of heaps */
int HeapSize(HP* php);3, Implementation of heap
It was mentioned in detail when explaining the implementation sequence table earlier. It is a cliche. The analysis of some interfaces here will not be interpreted in detail. If you can't remember, it is recommended to review the sequence table mentioned earlier.
🔗 Link: [data structure] detailed explanation of sequence table
0x00 heap initialization (HeapInit)
💬 Heap.h
#pragma once
#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
#include <stdbool.h>
typedef int HPDataType;
typedef struct Heap {
HPDataType* array; //Point to a dynamic array
int size; //Number of valid data
int capacity; //Size of capacity space
} HP;🔑 Interpretation: the actual structure of the heap is an array. We use an array to implement it. If we want it to support addition, deletion, query and modification, we can't use a static array, but a dynamic array. In this way, we can expand the capacity. There are size and capacity, which is similar to the sequence table. This is a very general structure.
💬 Heap.c
/* Heap initialization */
void HeapInit(HP* php) {
assert(php);
php->array = NULL;
php->capacity = php->size = 0;
}0x01 heap destruction (HeapDestroy)
💬 Heap.h
void HeapDestroy(HP* php);
💬 Heap.c
/* Heap destruction */
void HeapDestroy(HP* php) {
assert(php);
free(php->array);
php->capacity = php->size = 0;
}0x02 heap printing (HeapPrint)
💬 Heap.h
void HeapPrint(HP* php);
💬 Heap.c
/* Heap printing */
void HeapPrint(HP* php) {
int i = 0;
for (i = 0; i < php->size; i++) {
printf("%d ", php->array[i]);
}
printf("\n");
}0x03 Determine whether the heap is empty (HeapEmpty)
💬 Heap.h
/* Determine whether the heap is empty */ bool HeapIfEmpty(HP* hp);
💬 Heap.c
/* Determine whether the heap is empty */
bool HeapIfEmpty(HP* php) {
assert(php);
return php->size == 0; // If the size is 0, the heap is empty
}🔑 Interpretation: here, the Boolean property is cleverly used, and the size of the return array can be directly used. size == 0 is true, otherwise it returns false.
0x04 Heap insertion (HeapInit)
📌 Insert the core idea:
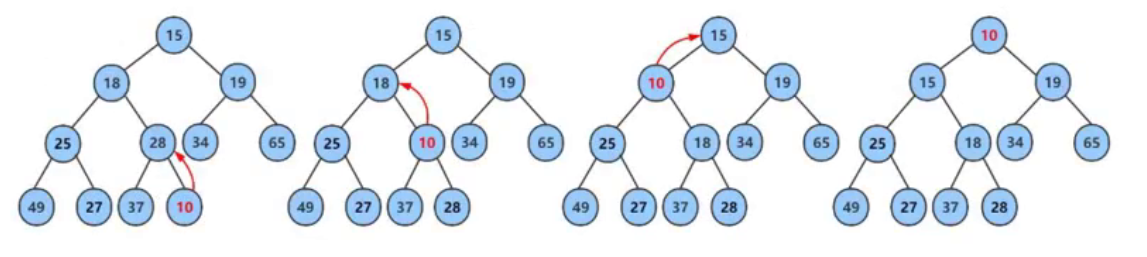
① Insert the element at the end of the heap, after the last child.
② After insertion, if the nature of the heap is damaged, adjust the newly inserted node up to the appropriate position along its father until it conforms to the nature of the heap.
Let's first solve the insertion function and implement the code of the next capacity increase part, so that we can pay more attention to the problem of heap insertion. We have also discussed this in detail in the sequence table, and we will review it here:
Check whether capacity increase is required (HeapCheckCapacity)
void HeapCheckCapacity(HP* php) {
if(php->size == php->capacity) {
int newCapacity = php->capacity == 0 ? 4 : (php->capacity * 2); //4 for the first time, and 2 times for other cases
HPDataType* tmpArray = (HPDataType*)realloc(php->array, sizeof(HPDataType) * newCapacity); // Array expansion
if(tmpArray == NULL) { //Check realloc
printf("realloc failed!\n");
exit(EXIT_FAILURE);
}
//Update their size
php->array = tmpArray;
php->capacity = newCapacity;
}
}🔑 Interpretation: refer to the explanation in the chapter of sequence table, which will not be repeated here.
According to the nature of the heap, if the heap and small heap are not satisfied, and the child is greater than the parent or the parent is greater than the child, we need to adjust from bottom to top to ensure that the heap is still the heap after insertion. The heap insertion data has no impact on other nodes, but may affect the relationship from it to the nodes on the root node path.
💭 give an example:
① For example, in the following case: the newly inserted is 60, and the child is greater than the parent (60 > 56), so it needs to be exchanged.

② There are more special cases: for example, the newly inserted ones are 100, 100 and 56. After the exchange, they have to be exchanged with 70.
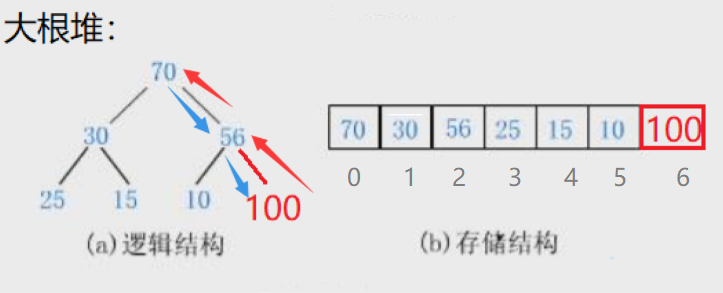
First assign the father to the child, then assign the child to the father, and then let the father go up to judge whether he is older than the father. If he is older, exchange. In order to deal with these situations, we need to write an "upward adjustment" algorithm (at worst, to the root stop):
Adjust up
void AdjustUp(int* arr, int child) {
assert(arr);
// First, calculate the subscript of the father according to the formula
int parent = (child - 1) / 2;
// Worst case: transfer to the root. child=parent ends when child is the root node (the root node is always 0)
while(child > 0) {
if(arr[child] > arr[parent]) { // If the child is larger than the father (not in line with the nature of the heap)
// Exchange their values
HPDataType tmp = arr[child];
arr[child] = arr[parent];
arr[parent] = tmp;
// Go up
child = parent;
parent = (child - 1) / 2;
} else { // If the child is smaller than the father (consistent with the nature of the heap)
// Jump out of loop
break;
}
}
}🔑 Interpretation:
① When designing the AdjustUp interface, we need to think about what value to receive first. Because we want to adjust the contents of the array, we need to pass in the array and receive it with int *. In addition, use child to receive the subscript of the value we just inserted as the starting position of the adjustment position.
② First, prevent the passed in array from being empty.
③ We must first determine the subscript of the child and the father. It is known that the child asks the father:
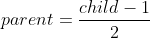 (the formula has been learned in the previous chapter)
(the formula has been learned in the previous chapter)
We already have the child subscript, because we transfer the starting position of the adjustment position, that is, the data just inserted, to the function and receive it as child. At this time, we define the parent variable and deduce the father's subscript according to the formula.
④ We've got the child and father's subscripts, and we can start the operation. First, analyze the worst case. The worst case is to adjust to the root position. child = parent, because the root node is always 0. When child is 0, the parent should be less than 0. Therefore, when child is the root node, it means that the adjustment has been completed. Here, the judgment condition of while is child > 0, As for why it is so awkward to take child > 0 as the condition instead of parent > = 0, we will talk about it in detail below.
⑤ After entering the loop, first if judge that if the value of child in the array is greater than the value of parent, it means that the child is greater than the father, which means that it does not conform to the nature of a lot. We're going to replace it. Here, we can create a tmp temporary variable of HPDataType type for exchange.
⑥ After the exchange, their values have been exchanged with each other. At this time, we need to change the direction of parent and child to let them continue to go up, so as to continue to judge. child = parent, and the new parent can be calculated again according to the formula.
⑦ The else part of the if is designed. If the child value of the array is greater than the parent value, it indicates that it conforms to the nature of a pile, Just break out of the loop.
❓ Why write the loop condition as: while(child) > 0) We need to see whether it is adjusted to the root. According to the normal idea, shouldn't we look at whether the parent is less than 0? while(parent >= 0)
💡 You can't write that! There is actually a problem with this. Let's take a value and see:
while(child > 0) ✅
while(parent >= 0) ❌
Let's analyze the process and take a value into the test: suppose 75 is inserted
[[start]
70
50 30 (p)
25 15 10 75* (c)
parent Finally equal to 2
[First time]
70 (p)
50 75* (c)
25 15 10 30
parent Finally equal to 0
[Last time]
(p)
75* (c)
50 70
25 15 10 30
parent Finally, it is equal to 0 (we want its result to be less than 0)
Why? The last time I went up,
child = parent; here child=0
parent = (child - 1) / 2;
(0 - 1) / 2 = 0 as a result parent It will still be 0
cause parent It will not be less than 0 at all!int main(void) {
int parent = (0 - 1) / 2;
printf("%d", parent);
return 0;
}🚩 Run result: 0
🔺 So we're going to use while(child > 0), which will not cause problems and will have the same effect as parent > = 0. Because when child= 0 indicates that the root has been touched.
⚡ Here we use exchange, because it is also necessary to delete the interface later. We might as well encapsulate it into an interface so that we can call it many times later:
Swap
void Swap(HPDataType* px, HPDataType* py) {
HPDataType tmp = *px;
*px = *py;
*py = tmp;
}void AdjustUp(int* arr, int child) {
assert(arr);
// First, calculate the subscript of the father according to the formula
int parent = (child - 1) / 2;
// Worst case: transfer to the root. child=parent ends when child is the root node (the root node is always 0)
while(child > 0) {
if(arr[child] > arr[parent]) { // If the child is larger than the father (not in line with the nature of the heap)
// Exchange their values
Swap(&arr[child],&arr[parent]); // Transmission address
// Go up
child = parent;
parent = (child - 1) / 2;
} else { // If the child is smaller than the father (consistent with the nature of the heap)
// Jump out of loop
break;
}
}
}Check whether the interfaces for capacity expansion and upward adjustment have been written. Now we can insert the heap:
💬 Heap.h
void HeapPush(HP* php, HPDataType x);
💬 Heap.c
void HeapPush(HP* php, HPDataType x) {
assert(php);
// Check whether capacity expansion is required
HeapCheckCapacity(php);
// insert data
php->array[php->size] = x;
php->size++;
// Adjust up [target array, data just inserted]
AdjustUp(php->array, php->size - 1);
}🔑 Interpretation:
① First check if php is empty.
② Check whether capacity expansion is required. Just call the HeapCheckCapacity interface we just implemented.
③ Then insert the data, which is the same as the tail insertion of the sequence table.
Finally, calling the AdjustUp interface, passing in the target array, and inserting the data. size - 1).
0x05 deletion of heap (HeapPop)
The deletion of heap is because we use a large heap to demonstrate when talking about heap insertion. Let's use a small heap to demonstrate first.
📌 The core idea of deletion: delete the heap, and delete the data at the top of the heap. Is to delete the root of the tree.
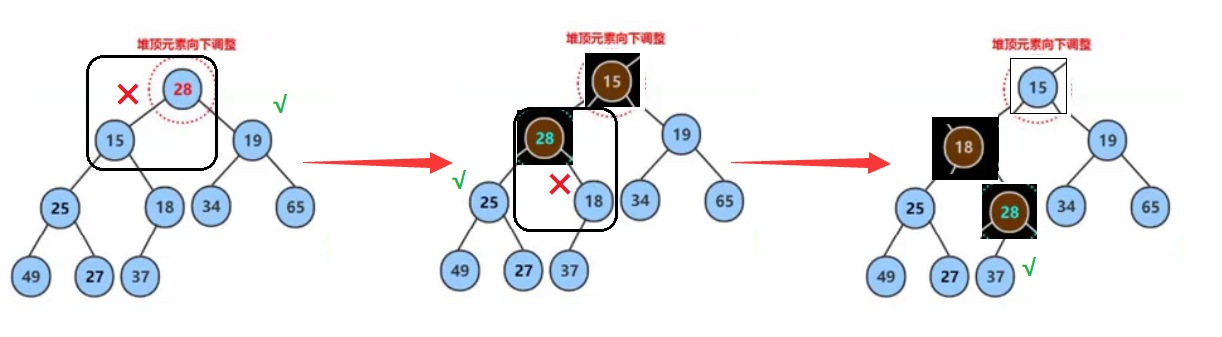
📚 Replace the data at the top of the heap with the last data, then delete the last data of the array, and then adjust the algorithm downward.
① Swap the top element of the heap with the last element in the heap.
② Deletes the last element in the heap.
③ Adjust the heap top element down to meet the heap characteristics.
Adjust it down, adjust it into a pile, and exchange it with the small one of the left and right children.
End condition (if one is true):
① Father 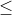 For small children, stop.
For small children, stop.
② Adjust to the leaf (because the leaf is characterized by no children, and the left child subscript is out of the range of the array, it does not exist).
SmallAdjustDown
void SmallAjustDown(int* arr, int n, int parent) {
int child = parent * 2 + 1; // The default is left child
while(child < n) { // Inside leaves
// Choose the primary and secondary children
if(child + 1 < n && arr[child + 1] < arr[child]) {
child = child + 1;
}
// If the child is smaller than the father (not in line with the nature of small piles)
if(arr[child] < arr[parent]) {
// Exchange their values
Swap(&arr[child], &arr[parent]);
// Go down
parent = child;
child = parent * 2 + 1;
} else { // If the child is larger than the father (in line with the nature of small piles)
// Jump out of loop
break;
}
}
}
🔑 Interpretation:
① Because we want to consider the left child or the right child, we can define two variables to record the left child and the child. But we can use a better method here. We only need to define a child. The specific implementation method is as follows: first, create a child. First, we default that it is the left child. Use the passed in parent to calculate the size of the child according to the formula:

Because we default to the left child for the time being, we need to check whether the left child is older or the right child is older after entering the loop. Here, we only need to add child + 1 according to the nature of the array to get the subscript of the right child, so as to facilitate our comparison. After the comparison, assign the child again. Take a child and give it to who when he is young.
② There are two end conditions (exit). The first end condition is that the father stops when he is smaller than the child, and the second end condition is that chi is adjusted to leaf. Therefore, according to the end condition we analyzed, the loop body judgment part ends when the leaf is adjusted. We accept n, that is, the size of the array. As long as the child exceeds the size of the array (child > n), it ends. This is the first exit.
③ After entering the cycle, compare the left child and the right child, which is smaller, and the child will be delivered to who. It should also be noted that children do not exist. If child + 1 is greater than N, it means that children do not exist. Therefore, when we write the if judgment condition again, we should pay attention to the following restrictions by adding a condition of child + 1 < n:
if(child + 1 < n && arr[child + 1] < arr[child]) {...}④ After identifying the younger children, we can start comparing the size of the child and the father. If the child is smaller than the father, it does not conform to the nature of small piles, and we have to exchange their values. Here, we can directly call the Swap interface we just wrote, which is why we need to write the code of the exchange part as a function when writing upward adjustment.
⑤ After the exchange, their values have been exchanged with each other. At this time, we need to change the direction of parent and child and let them go down. parent = child, child Again, calculate the new value according to the formula Child.
⑥ The else part of if is designed. If the child value of the array is greater than the parent value, it indicates that it conforms to the nature of small heap, Just break out of the loop. This is the second exit.
After the interface adjusted from bottom to top is written, we can now delete the heap:
💬 Heap.h
void HeapPop(HP* php);
💬 Heap.c
void HeapPop(HP* php) {
assert(php);
assert(!HeapIfEmpty(php));
// Delete data
Swap(&php->array[0], &php->array[php->size - 1]);
php->size--;
// Adjust down [target array, size of array, start position of adjustment position]
SmalljustDown(php->array, php->size, 0);
}🔑 Interpretation:
① First check if php is empty.
② Because there must be something to delete for deletion, here we must check whether it is empty and call HeapIfEmpty , The logical inverse operator asserts that the array is not empty.
③ Because deleting the heap deletes the data at the top of the heap, we need to delete the data directly according to our experience.
Finally, call AdjustDown. Interface, pass in the target array, the size of the array, and the starting position (i.e. 0).
❓ What if we want to change it into a lot?
💡 Just change the judgment conditions:
① Choose the older child.
② The small pile is that all fathers are smaller than children, and the large pile is that all fathers are larger than children. Let's change it:
BigAdjustDown
void BigAdjustDown(int* arr, int n, int parent) {
int child = parent * 2 + 1; // The default is left child
while (child < n) { // Inside leaves
// Choose the older of the left and right children
if (child + 1 < n && arr[child + 1] > arr[child]) {
child++;
}
if (arr[child] > arr[parent]) { // If the child is larger than the father (not in line with the nature of the father)
// Exchange their values
Swap(&arr[child], &arr[parent]);
// Go down
parent = child;
child = parent * 2 + 1;
}
else { // If the child is smaller than the father (in line with the nature of the father)
// Jump out of loop
break;
}
}
}🔑 Interpretation: it's very simple. Just change the judgment conditions.
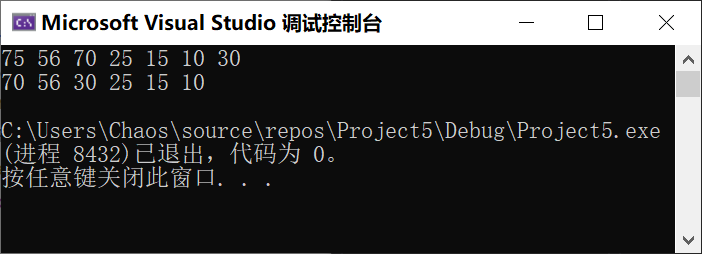
💬 Test.c
Let's test some of the code we just wrote.
#define _CRT_SECURE_NO_WARNINGS 1
#include "Heap.h"
void HeapTest1() {
// Big root pile
int a[] = { 70, 56, 30, 25,15,10,75 };
HP hp;
HeapInit(&hp);
for (int i = 0; i < sizeof(a) / sizeof(a[0]); ++i) {
HeapPush(&hp, a[i]);
}
HeapPrint(&hp);
HeapPop(&hp);
HeapPrint(&hp);
}
int main()
{
HeapTest1();
return 0;
}🚩 Operation results:
0x06 return heap top data (HeapTop)
💬 Heap.h
HPDataType HeapTop(HP* php);
💬 Heap.c
/* Return heap top data */
HPDataType HeapTop(HP* php) {
assert(php);
assert(!HeapIfEmpty(php));
return php->array[0];
}🔑 Interpretation:
① First check the incoming Whether php is empty, and also prevent no data in the heap.
② Return to the top of the heap. The top of the heap is the root. The subscript of the root is 0. Return to the root.
0x07 Count the number of heaps (HeapSize)
💬 Heap.h
HPDataType HeapTop(HP* php);
💬 Heap.c
/* Count the number of heaps */
int HeapSize(HP* php) {
assert(php);
return php->size;
}🔑 Interpretation:
① First check the incoming Whether php is empty.
② Instead of counting the number of heaps, it is better to return the number of heaps, because there is no need to count at all. It is done by directly returning size.
4, Complete code
💬 Heap.h
#define _CRT_SECURE_NO_WARNINGS 1
#pragma once
#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
#include <stdbool.h>
typedef int HPDataType;
typedef struct Heap {
HPDataType* array; //Point to a dynamic array
int size; //Number of valid data
int capacity; //Size of capacity space
} HP;
/* Heap initialization */
void HeapInit(HP* php);
/* Heap destruction */
void HeapDestroy(HP* php);
/* Heap printing */
void HeapPrint(HP* php);
/* Determine whether the heap is empty */
bool HeapIfEmpty(HP* hp);
/* Heap insertion */
void HeapPush(HP* php, HPDataType x);
/* Check capacity */
void HeapCheckCapacity(HP* php);
/* Exchange function */
void Swap(HPDataType* px, HPDataType* py);
/* Large root pile up regulation */
void BigAdjustUp(int* arr, int child);
/* Small root pile up regulation */
void SmallAdjustUp(int* arr, int child);
/* Deletion of heap */
void HeapPop(HP* php);
/* Small root pile down regulation*/
void SmallAdjustDown(int* arr, int n, int parent);
/* Large root pile down regulation */
void BigAdjustDown(int* arr, int n, int parent);
/* Return heap top data*/
HPDataType HeapTop(HP* php);
/* Count the number of heaps */
int HeapSize(HP* php);💬 Heap.c
#define _CRT_SECURE_NO_WARNINGS 1
#include "Heap.h"
/* Heap initialization */
void HeapInit(HP* php) {
assert(php);
php->array = NULL;
php->size = php->capacity = 0;
}
/* Heap destruction */
void HeapDestroy(HP* php) {
assert(php);
free(php->array);
php->capacity = php->size = 0;
}
/* Heap printing */
void HeapPrint(HP* php) {
for (int i = 0; i < php->size; i++) {
printf("%d ", php->array[i]);
}
printf("\n");
}
/* Determine whether the heap is empty */
bool HeapIfEmpty(HP* php) {
assert(php);
return php->size == 0; // If the size is 0, the heap is empty
}
/* Heap insertion */
/* Check capacity */
void HeapCheckCapacity(HP* php) {
if (php->size == php->capacity) {
int newCapacity = php->capacity == 0 ? 4 : (php->capacity * 2); //4 for the first time, and 2 times for other cases
HPDataType* tmpArray = (HPDataType*)realloc(php->array, sizeof(HPDataType) * newCapacity); // Array expansion
if (tmpArray == NULL) { //Check realloc
printf("realloc failed!\n");
exit(EXIT_FAILURE);
}
//Update their size
php->array = tmpArray;
php->capacity = newCapacity;
}
}
/* Exchange function */
void Swap(HPDataType* px, HPDataType* py) {
HPDataType tmp = *px;
*px = *py;
*py = tmp;
}
/* Large root pile up regulation */
void BigAdjustUp(int* arr, int child) {
assert(arr);
// First, calculate the subscript of the father according to the formula
int parent = (child - 1) / 2;
// Worst case: transfer to the root. child=parent ends when child is the root node (the root node is always 0)
while (child > 0) {
if (arr[child] > arr[parent]) { // If the child is larger than the father (not in line with the nature of the heap)
// Exchange their values
Swap(&arr[child], &arr[parent]);
// Go up
child = parent;
parent = (child - 1) / 2;
} else { // If the child is smaller than the father (consistent with the nature of the heap)
// Jump out of loop
break;
}
}
}
/* Small root pile up regulation */
void SmallAdjustUp(int* arr, int child) {
assert(arr);
// First, calculate the subscript of the father according to the formula
int parent = (child - 1) / 2;
// Worst case: transfer to the root. child=parent ends when child is the root node (the root node is always 0)
while (child > 0) {
if (arr[child] < arr[parent]) { // If the child is larger than the father (not in line with the nature of the heap)
// Exchange their values
Swap(&arr[child], &arr[parent]);
// Go up
child = parent;
parent = (child - 1) / 2;
} else { // If the child is smaller than the father (consistent with the nature of the heap)
// Jump out of loop
break;
}
}
}
void HeapPush(HP* php, HPDataType x) {
assert(php);
// Check whether capacity expansion is required
HeapCheckCapacity(php);
// insert data
php->array[php->size] = x;
php->size++;
// Adjust upward [target array, start position of adjustment position (data just inserted)]
BigAdjustUp(php->array, php->size - 1);
}
/* Deletion of heap */
/* Small root pile down regulation*/
void SmallAdjustDown(int* arr, int n, int parent) {
int child = parent * 2 + 1; // The default is left child
while (child < n) { // Inside leaves
// Choose the primary and secondary children
if (child + 1 < n && arr[child + 1] < arr[child]) {
child++;
}
if (arr[child] < arr[parent]) { // If the child is smaller than the father (not in line with the nature of small piles)
// Exchange their values
Swap(&arr[child], &arr[parent]);
// Go down
parent = child;
child = parent * 2 + 1;
} else { // If the child is larger than the father (in line with the nature of small piles)
// Jump out of loop
break;
}
}
}
/* Large root pile down regulation */
void BigAdjustDown(int* arr, int n, int parent) {
int child = parent * 2 + 1; // The default is left child
while (child < n) { // Inside leaves
// Choose the older of the left and right children
if (child + 1 < n && arr[child + 1] > arr[child]) {
child++;
}
if (arr[child] > arr[parent]) { // If the child is larger than the father (not in line with the nature of the father)
// Exchange their values
Swap(&arr[child], &arr[parent]);
// Go down
parent = child;
child = parent * 2 + 1;
} else { // If the child is smaller than the father (in line with the nature of the father)
// Jump out of loop
break;
}
}
}
void HeapPop(HP* php) {
assert(php);
assert(!HeapIfEmpty(php));
// Delete data
Swap(&php->array[0], &php->array[php->size - 1]);
php->size--;
// Adjust down [target array, size of array, start position of adjustment position]
/* SmallAdjustDown(php->array, php->size, 0); */
BigAdjustDown(php->array, php->size, 0);
}
/* Return heap top data */
HPDataType HeapTop(HP* php) {
assert(php);
assert(!HeapIfEmpty(php));
return php->array[0];
}
/* Count the number of heaps */
int HeapSize(HP* php) {
assert(php);
return php->size;
}
reference material:
Microsoft. MSDN(Microsoft Developer Network)[EB/OL]. []. .
Baidu Encyclopedia [EB / OL]. [] https://baike.baidu.com/.
📌 Author: Wang Yiyou
📃 Update: November 26, 2021
❌ Corrigendum: None
📜 Statement: due to the limited level of the author, it is inevitable that there are errors and inaccuracies in this article. I also want to know these errors. I sincerely hope the readers can criticize and correct them!
End of this chapter.