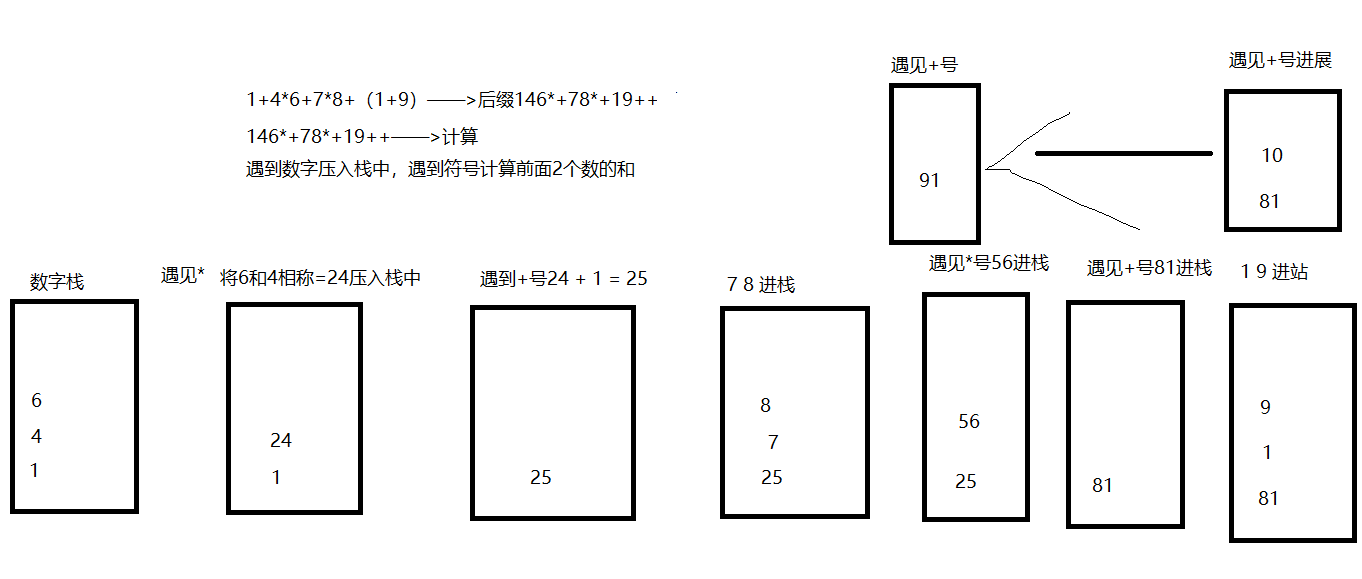
I. Analysis of String Expressions

The z-string expression is a very typical column in the application of stack structure, and its algorithm design idea makes full use of the characteristics of stack.

For example, "1+8*9+(4+5)*7" completes the calculation of string expressions in two steps.

1. Converting a suffix to a suffix

According to the priority of (*/+-), create two stacks to store numbers and symbols, traverse from the first element, encounter numbers into the digital stack, encounter symbols into the symbolic stack, if the top symbol priority is higher or lower than this symbol priority, then push the top element into the digital stack until the elements of the symbol stack are completely traversed. The part is pushed into the stack.

2. Compute suffix expressions

Traversing through all elements, encountering numeric numbers pushed into the new stack, encountering symbols that take this symbol as the operator of the first two digits, the calculation results are pushed into the new stack until the calculation is completed.

Schematic diagram:

II. Implementation of Source Code

#include <iostream>
#include <cstdio>
#include <cstring> 
#include <cstdlib>
const int  SIZE = 100; // Initial capacity of stack
const int  ADDSIZE = 5; // Unit Increase Capacity of Stack
using namespace std;// Namespace
const int INF = -0xfffffff;// Used to prevent embarrassment when empty stack, return an address that can not be read, embarrassing the reader;
template <class T>
struct Strack
{
	T *top;// A pointer at the top of the stack
	T *base;// A pointer at the bottom of the stack
	int strackSize;//Stack capacity
	void init()//Initialization of stacks
	{
		base = (T *)malloc(SIZE * sizeof(T));//Allocated memory
		top = base;
		strackSize = SIZE;
	}

	T Top()
	{// Returns the top element of the stack
		if (top == base)
			return INF;// Return to an embarrassing address
		return *(top - 1);
	}

	bool pop()
	{// Delete stack top elements
		if (top == base)
			return false;
		top--;
		return true;
	}

	void push(T x)
	{//Stack top insertion element
		if (isPull()) {//If memory is insufficient to reallocate memory
			base = (T *)realloc(base, (strackSize + ADDSIZE)*(sizeof(T)));
			top = base + strackSize;
			strackSize += ADDSIZE;
		}
		*top++ = x;
	}

	bool isEmpty()
	{//Determine whether the stack is empty
		if (top == base)
			return true;
		return false;
	}

	bool isPull()//Completion function
	{
		if (top - base == strackSize)// push one at a time so full when top - base = strackSize
			return true;
		else
			return false;
	}
};

int compareNumber(char x)//Used to compare the precedence of symbols
{
	if (x == '+' || x == '-')
		return 0;
	if (x == '*' || x == '/')
		return 1;
	return -1;
}

void change(char *mid, char *suxfix)//Converting an infix expression to a suffix expression     
{
	int i = 0, len = strlen(mid), mid_index = 0;
	char c;
	Strack<char >intElements;// int data set
	intElements.init();
	intElements.push('#'); // Special Symbols Used to Distinguish Elements
	while (i < len)
	{
		if (mid[i] == '(')
		{
			intElements.push(mid[i]);
			i++;
		}
		else if (mid[i] == ')')
		{
			while (intElements.Top() != '(')
			{
				suxfix[mid_index++] = intElements.Top();
				suxfix[mid_index++] = ' ';
				intElements.pop();
			}
			intElements.pop();
			i++;
		}
		else if (mid[i] == '+' || mid[i] == '-' || mid[i] == '/' || mid[i] == '*')
		{
			while (compareNumber(intElements.Top()) >= compareNumber(mid[i]))
			{
				suxfix[mid_index++] = intElements.Top();
				suxfix[mid_index++] = ' ';
				intElements.pop();
			}
			intElements.push(mid[i]);
			i++;
		}
		else if (mid[i] >= '0'&&mid[i] <= '9')
		{
			while (mid[i] >= '0'&&mid[i] <= '9')
			{
				suxfix[mid_index++] = mid[i];
				i++;
			}
			suxfix[mid_index++] = ' ';
		}
		else
		{

		}
	}
	while (intElements.Top() != '#') {
		suxfix[mid_index++] = intElements.Top();
		suxfix[mid_index++] = ' ';
		intElements.pop();
	}
	suxfix[mid_index] = 0;
}

double countSuxfix(char *suxfix)//Compute suxfix suffix expression
{
	int len = strlen(suxfix);
	double x;
	Strack <int >intElements;
	intElements.init();
	int i = 0;
	while (i<len) {
		if (suxfix[i] == ' ')// Jump-out loop for expression valid character set exhaustion
		{
			i++;
			continue;
		}
		switch (suxfix[i])
		{
		case '+':
			x = intElements.Top();//According to the schematic diagram
			intElements.pop();
			x = intElements.Top() + x;
			intElements.pop(); i++;
			break;
		case '-':
			x = intElements.Top();
			intElements.pop();
			x = intElements.Top() - x;
			intElements.pop();
			i++;
			break;
		case '*':
			x = intElements.Top();
			intElements.pop();
			x = intElements.Top()*x;
			intElements.pop();
			i++;
			break;
		case '/':
			x = intElements.Top();
			intElements.pop();
			x = intElements.Top() / x;
			intElements.pop();
			i++;
			break;
		default:
		{
			x = 0;
			while (suxfix[i] >= '0'&&suxfix[i] <= '9') {
				x = x * 10 + suxfix[i] - '0';// Two consecutive numbers, the first * 10, and so on
				i++;
			}
		}
		}

		intElements.push(x);
	}
	return intElements.Top();
}
int main()
{
	char str[1000];
	char newStr[1000];
	scanf("%s", str);
	change(str, newStr);
	cout << newStr << endl;
	cout << countSuxfix(newStr) << endl;
	return 0;
}

--------------------------------------------------------------------------over-----------------------------------------------------------------------------------------