Traversal of binary tree
In this paper, we calculate a data collation, which is a binary tree traversal method, including PreOrder, InOrder, PostOrder, width first search, depth first search
The example traverses a binary tree: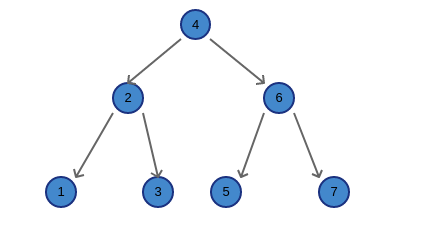
Binary tree node format:
class TreeNode:
def __init__(self, val):
self.val = val
self.left = self.right = None1. PreOrder traversal
First traverse the root node, then the left subtree, and finally the right subtree
def pre_order(root: TreeNode) -> list:
if not root:
return []
return [root.val] + pre_order(root.left) + pre_order(root.right)
#### Ergodic result
## [4, 2, 1, 3, 6, 5, 7]2. Middle order traversal InOrder
First traverse the left subtree, then the root node, and finally the right subtree,
def in_order(root: TreeNode) -> list:
if not root:
return []
return in_order(root.left) + [root.val] + in_order(root.right)
#### Ergodic result
## [1, 2, 3, 4, 5, 6, 7]3. Post order traversal
First traverse the left subtree, then the right subtree, and finally the root node
def post_order(root: TreeNode) -> list:
if not root:
return []
return post_order(root.left) + post_order(root.right) + [root.val]
#### Ergodic result
## [1, 3, 2, 5, 7, 6, 4]4. Breadth first search
Traversing binary tree by level
import collections
def breadth_first_search(root: TreeNode) -> list:
"""
//This is just the breadth first traversal of binary tree. Unlike the breadth first traversal of graph, it returns the traversal order of binary tree
:param root: TreeNode
:return: list
"""
if not root:
return []
queue = collections.deque() # Apply for a two terminal queue
queue.append(root)
result = []
# visited = set(root) # Because it's the structure of a tree, there won't be any repetition as long as you go down
while queue:
level_size = len(queue)
for _ in range(level_size):
node = queue.popleft() # Here it goes out from the left, and it will be added to the end when it is added below. If it goes out from the right, it will be push ed in from the left below
result.append(node.val)
if node.left:
queue.append(node.left)
if node.right:
queue.append(node.right)
return result
### Output result
## [4, 2, 6, 1, 3, 5, 7]5. Depth first search
Is an algorithm for traversing or searching trees or graphs. The nodes of the tree are traversed along the depth of the tree, and the branches of the tree are searched as deep as possible. When all the edges of node v have been explored, the search will go back to the starting node of the edge where node v is found. This process continues until all nodes reachable from the source node have been found
def depth_first_search(root: TreeNode, result=[]) -> list:
"""
//Binary tree breadth first traversal, return breadth traversal order
:param root:
:param result:
:return:
"""
if not root:
return []
result.append(root.val)
depth_first_search(root.left, result)
depth_first_search(root.right, result)
return result
### Output result
## [4, 2, 1, 3, 6, 5, 7]