I. overview
1. Classification of sorting
1.1 internal sorting
- Insert sort: direct insert sort Hill sort half insert sort (not commonly used)
- Exchange sort: Bubble Sort quick sort
- Select sort: simple select sort heap sort
- Merge sort
- Radix sorting
1.2 external sorting
- Multiway merge sort
Commonly used is internal sorting, but also the focus of computer research objects.
2. Comparison of various algorithms
| Algorithm type | Best case (time) | Average (time) | Worst case (time) | Spatial complexity | Stable or not |
| Direct insert sort | O(n) | O(n^2) | O(n^2) | O(1) | Yes. |
| Bubble sort | O(n) | O(n^2) | O(n^2) | O(1) | Yes. |
| Simple selection sorting | O(n^2) | O(n^2) | O(n^2) | O(1) | No |
| Shell Sort | O(1) | No | |||
| Quick sort | O(nlog2n) | O(nlog2n) | O(n^2) | O(log2n) | No |
| Heap sort | O(nlog2n) | O(nlog2n) | O(nlog2n) | O(1) | No |
| 2-way merge and sort | O(nlog2n) | O(nlog2n) | O(nlog2n) | O(n) | Yes. |
| Radix sorting | O(d(n+r)) | O(d(n+r)) | O(d(n+r)) | O(r) | Yes. |
From the table, it is not difficult to draw the following conclusions:
- The unstable algorithms are: simple selection sort, Hill sort, heap sort, fast sort
- Direct insertion sorting with Hill sorting independent of the number of sorting passes and the initial sequence
- Simple selective sorting, merging sorting and cardinal sorting, in which the number of element comparisons is independent of the initial sequence
- The time complexity of direct insertion sorting is the lowest when the elements are ordered
- The highest time complexity of quick sorting is O(n^2) when the elements are in order or in reverse order
2, Direct insert sort
def: for a given set of records, the first record is initially assumed to be an ordered sequence, and the rest are unordered; then, starting from the second record, the current processed records are inserted into the previous ordered sequence according to the size of the record, until the last record is inserted into the ordered sequence.

#include <stdio.h>
void InsertSort(int array[], int len)
{
int i, j, temp;
for(i = 1; i < len; i++)
{
temp = array[i];
for(j = i - 1; j >= 0; j--)
{
if(temp < array[j])
{
array[j + 1] = array[j];
}
else
{
break;
}
}
array[j + 1] = temp;
}
}
int main()
{
int i = 0;
int a[] = {8, 2, 5, 3, 6, 7, 1, 9, 0};
int length = sizeof(a) / sizeof(a[0]);
InsertSort(a, length);
for(i = 0; i < length; i++)
{
printf("%d ", a[i]);
return 0;
}3, Hill sort
def: Hill sort is also called "reduce incremental sort". The basic principle is: first, the elements to be sorted are divided into multiple subsequences, so that the number of elements in each subsequence is relatively small. Each subsequence is directly inserted and sorted. After the whole sequence to be sorted is "basically ordered", all elements are directly inserted and sorted once.

#include <stdio.h>
void ShellSort(int array[], int len)
{
int i, j, temp, h;
for(h = len / 2; h > 0; h = h / 2)
{
for(i = h; i < len; i++)
{
temp = array[i];
for(j = i - h; j >= 0; j -= h)
{
if(temp < array[j])
{
array[j + h] = array[j];
}
else
{
break;
}
}
array[j + h] = temp;
}
}
}
int main()
{
int i = 0;
int a[] = {8, 2, 5, 3, 6, 7, 1, 9, 0};
int length = sizeof(a) / sizeof(a[0]);
ShellSort(a, length);
for(i = 0; i < length; i++)
{
printf("%d ", a[i]);
}
return 0;
}4, Bubble sorting
Hey, ha, this is too simple. Just roll up the code
#include <stdio.h>
void BubbleSort(int array[], int len)
{
int i, j;
int temp;
for (i = 0; i < len -1; ++i)
{
for (j = len - 1; j > i; --j)
{
if (array[j] < array[j - 1])
{
temp = array[j];
array[j] = array[j - 1];
array[j - 1] = temp;
}
}
}
}
int main()
{
int i = 0;
int a[] = {29, 18, 87, 56, 3, 27};
int length = sizeof(a) / sizeof(a[0]);
BubbleSort(a, length);
for (i = 0; i < length; i++)
{
printf("%d ", a[i]);
}
printf("\n");
return 0;
}5, Simple selection sorting
def: for a given set of records, after the first round of comparison, the minimum records are obtained, and then the records are exchanged with the position of the first record; then the other records excluding the first record are sorted in the second round, and the minimum records are obtained and the position of the second record is exchanged; repeat the process until only one record is compared.

#include <stdio.h>
void SelectSort(int *num, int n)
{
int i, j;
int tmp = 0, min = 0;
for(i = 0; i < n - 1; i++)
{
min = i;
for(j = i + 1; j < n; j++)
{
if(num[j] < num[min])
{
min = j;
}
}
if(min != i)
{
tmp = num[i];
num[i] = num[min];
num[min] = tmp;
}
}
}
int main()
{
int i, len;
int num[] = {4, 8, 2, 4, 0, 9, 1, 3, 5};
len = sizeof(num) / sizeof(num[0]);
SelectSort(num, len);
for(i = 0; i < len; i++)
{
printf("%d ", num[i]);
}
return 0;
}Vi. quick sorting
def: adopt the idea of "divide and rule", divide the big into the small, and the small into the smaller. For a given set of records, the original sequence is divided into two parts after a sequence, in which all records in the first part are smaller than those in the second part, and then the records in the first part and the second part are sorted quickly in turn, and the process is recursive until all records in the sequence are in order.
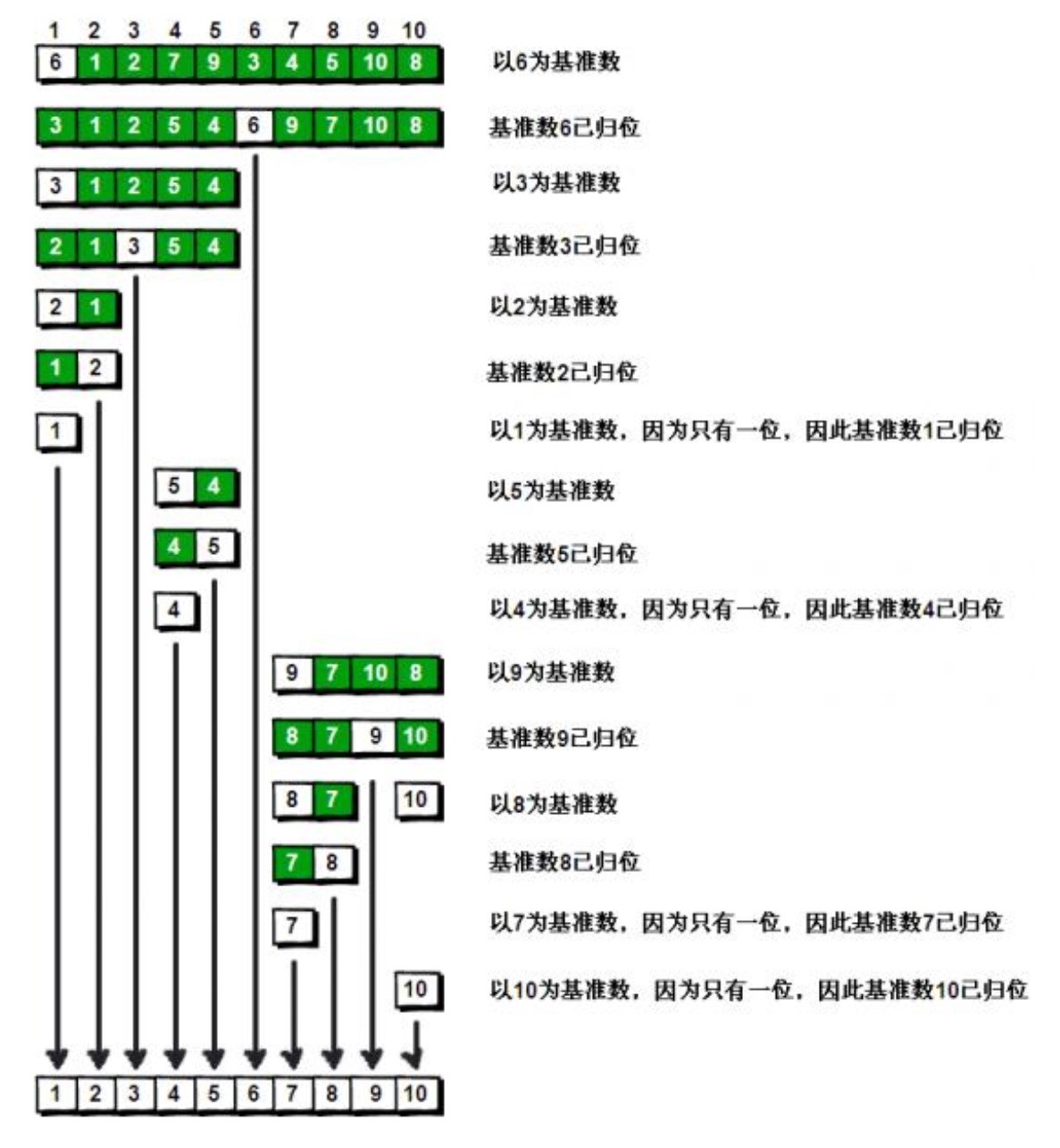
#include <stdio.h>
int a[30], n;
void QuickSort(int left, int right)
{
int i, j, tmp, tmp1;
i = left;
j = right;
if(left >= right)
{
return;
}
while(i < j)
{
while(a[j] >= a[left] && i < j) //left as reference
{
j--;
}
while(a[i] <= a[left] && i < j)
{
i++;
}
if(i < j)
{
tmp = a[i];
a[i] = a[j];
a[j] = tmp;
}
}
tmp1 = a[i];
a[i] = a[left];
a[left] = tmp1;
QuickSort(left, i - 1);
QuickSort(i + 1, right);
}
int main()
{
int i;
printf("Please input n:\n");
scanf("%d", &n);
printf("Please input number:\n");
for(i = 1; i <= n; i++)
{
scanf("%d", &a[i]);
}
QuickSort(1, n);
for(i = 1; i <= n; i++)
{
printf("%d ", a[i]);
}
return 0;
}7, Heap sort
By transforming the common complete binary tree into a heap, the minimum value can be obtained; the minimum value can be output; by deleting the root node and continuing to transform the remaining tree into a heap, the secondary small value can be obtained; the secondary small value can be output; by repeating the transformation, the secondary small value and the secondary small value can be output until all nodes are output, and a sequence can be obtained.
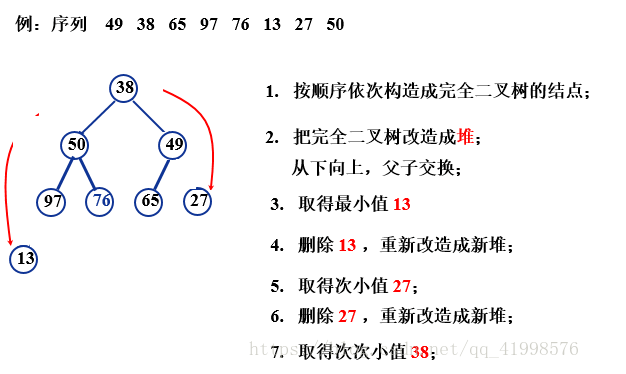
The steps of adding a node to the heap are: putting the last node into the heap according to the order from the root node to the node.
#Include < stdio. H > / / it is suitable for large amount of data (construction wastes time)
void AdjustMinHeap(int *array, int pos, int len)
{
int tmp, child;
for(tmp = array[pos]; 2 * pos + 1 <= len; pos = child)
{
child = 2 * pos + 1;
if(child < len && array[child] > array[child + 1])
{
child++;
}
if(array[child] < tmp)
{
array[pos] = array[child];
}
else
{
break;
}
}
array[pos] = tmp;
}
void Swap(int *a, int *b)
{
int temp;
temp = *a;
*a = *b;
*b = temp;
}
void HeapSort(int *array, int len)
{
int i;
for(i = len/2 - 1; i >= 0; i--)
{
AdjustMinHeap(array, i, len - 1);
}
for(i = len - 1; i >= 0; i--)
{
Swap(&array[0], &array[i]);
AdjustMinHeap(array, 0, i - 1);
}
}
int main()
{
int i;
int array[] = {0, 13, 14, 1, 18, 27};
int length = sizeof(array) / sizeof(array[0]);
HeapSort(array, length);
for(i = 0; i < length; i++)
{
printf("%d ", array[i]);
}
return 0;
}8, Merge sort
def:
Using recursion and divide and conquer technology, the data sequence is divided into smaller and smaller half sub tables, then the half sub tables are sorted, and finally the ordered half sub tables are merged into larger and larger ordered sequences by recursion steps. For a given set of records, first merge two adjacent subsequences with length of 1 to get n/2 ordered subsequences with length of 2 or 1. After merging the two records, repeat the process until an ordered sequence is obtained.

#include <stdio.h>
#include <stdlib.h>
void Merge(int array[], int start, int middle, int end)
{
int i, j, k, n1, n2;
n1 = middle - start + 1;
n2 = end - middle;
int *L = (int *)malloc(n1 * sizeof(int));
int *R = (int *)malloc(n2 * sizeof(int));
for (i = 0, k = start; i < n1; i++, k++)
{
L[i] = array[k];
}
for (i = 0, k = middle + 1; i < n2; i++, k++)
{
R[i] = array[k];
}
for (k = start, i = 0, j = 0; i < n1 && j < n2; k++)
{
if (L[i] < R[j])
{
array[k] = L[i];
i++;
}
else
{
array[k] = R[j];
j++;
}
}
if (i < n1)
{
for (j = i; j < n1; j++, k++)
{
array[k] = L[j];
}
}
if (j < n2)
{
for (i = j; i < n2; i++, k++)
{
array[k] = R[i];
}
}
}
void MergeSort(int array[], int start, int end)
{
int middle;
int i;
if (start < end)
{
middle = (start + end) / 2;
MergeSort(array, start, middle);
MergeSort(array, middle + 1, end);
Merge(array, start, middle, end);
}
}
int main()
{
int i = 0;
int a[] = {49, 38, 65, 97, 76, 13, 27};
int length = sizeof(a) / sizeof(a[0]);
MergeSort(a, 0, length -1);
for (i = 0 ; i < length; i++)
{
printf("%d ", a[i]);
}
printf("\n");
return 0;
}9, Cardinality sort
Steps:
(1) For allocation, start from the bits, and put them into buckets 0-9 according to the bit value (0-9) (for example, if the number of bits is 3, put them into buckets 3)
(2) Collect, and then put the data placed in buckets 0-9 into the array in order
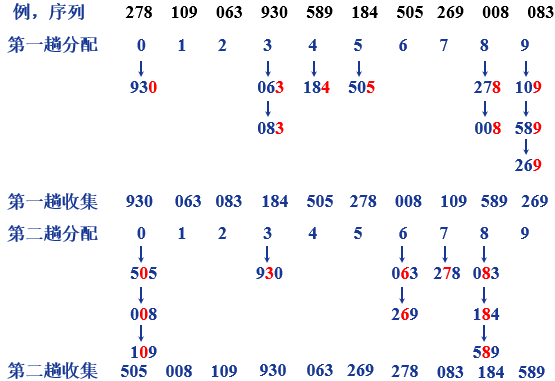
#include <stdio.h>
int Getmax(int *a, int n)
{
int i, max;
max = a[0];
for(i = 0; i < n; i++)
{
if(max < a[i])
{
max = a[i];
}
}
return max;
}
int countsort(int *a,int n, int exp)
{
int output[n];
int buckets[10] = {0};
int i;
for(i = 0; i < n; i++)
{
buckets[(a[i] / exp) % 10]++;
}
for(i = 1; i < n; i++)
{
buckets[i] += buckets[i - 1];
}
for(i = n - 1; i >= 0; i--)
{
output[buckets[(a[i] / exp) % 10] - 1] = a[i];
buckets[(a[i] / exp) % 10]--;
}
for(i = 0; i < n; i++)
{
a[i] = output[i];
}
return 1;
}
int Radixsort(int *a, int n)
{
int exp;
int max = Getmax(a, n);
for(exp = 1; (max / exp) > 0; exp *= 10 )
{
countsort(a,n,exp);
}
return 1;
}
int main()
{
int i;
int a[] = {278, 109, 63, 930, 589, 184, 505, 269, 8, 83};
int len = sizeof(a) / sizeof(a[0]);
Radixsort(a, len);
for(i = 0; i < len; i++)
{
printf("%d ", a[i]);
}
return 0;
}

