Although there is a sort() function in python that can easily sort lists and tuples in one sentence, in order to better understand the algorithm and data structure, Hanzhou has implemented six commonly used sorting algorithms in Python. The first three algorithms have time complexity of O(n^2) and the last three have time complexity of O (logn). If there are any shortcomings, please correct them.

1. Insert sort

The basic operation of insertion sorting is to insert a data into the ordered data,
Then a new ordered data is obtained, which can be used to sort a small amount of data;
First, take the first one as the ordered one, then insert it into the front and sort it every time

def insert_sort(list):
    for i in range(len(list)):#Traverse the list one by one and insert the ith element
        for j in range(i):#Treat the first i-1 element as an ordered list, and insert the i-th
            if list[i] < list[j]:#Compare the elements to be sorted with the ordered list in turn. If the larger one is found, insert
                list.insert(j, list.pop(i))#Pop up this element from the original list and insert it into the new location of the original list
                break#If there is no insertion at the end of the loop, the element position is appropriate
    return list

2. Bubble sorting

It repeatedly visited the sequence to be sorted,
Compare two elements at a time and swap them if they are out of order.
The work of the interview series is repeated until there is no need to exchange,
That is to say, the sequence has been sorted.
The name of this algorithm comes from the fact that the smaller the element, the more slowly it will "float" to the top of the sequence through exchange.

def bubble_sort(list):
    for i in range(len(list)):#All elements need to be bubbled, record the number of bubbling times, and take a picture of each element
        for j in range(len(list)-i-1):#Bubble unsorted elements
            if list[j]>list[j+1]:#If the element is larger
                list[j],list[j+1]=list[j+1],list[j]#Swap positions, put them in the back
    return list

3. Select Sorting

First, find the smallest (large) element in the unsorted sequence and store it at the beginning of the sorted sequence,
Then, continue to look for the smallest (largest) element from the remaining unsorted elements,
It is then placed at the end of the sorted sequence.
And so on until all elements are sorted.

def selection_sort(list):
	finish=[]#Ordered list
    while list:#When the list is not empty
        k=0#Record the position of the minimum value for each cycle
        for i in range(1,len(list)):#Find the minimum value in the existing unordered list
            if list[k]>list[i]:
                k=i#Update minimum position
        finish.append(list.pop(k))#Pop up the minimum value and add it to the sequence table
    return finish

4. Hill sorting

Hill sorting is to group records by a certain increment of subscript, and use direct insertion sorting algorithm to sort each group;
As the increment decreases, each group contains more and more keywords,
When the increment is reduced to 1, the whole file is just divided into a group, and the algorithm is terminated
(when understanding the following code snippet, it is recommended to substitute the code from i=0 for drawing comprehension)

def shell_sort(list):
	gap=len(list)#Initial increment length, set as table length
    while gap>1:#Exit sorting when increment is 1
        gap//=2#Halve increments
        for i in range(gap,len(list)):#Insert and sort each group. The original array is divided into gap groups with gap elements at the beginning
            for j in range(i%gap,i,gap):#Sort the first i elements in each group. The interval of data in each group is incremental gap
                if list[j]>list[i]:#If the size order is not correct, exchange, and ensure that list[i] is the largest element in each group
                    list[j],list[i]=list[i],list[j]
    return list

5. Merge and sort

Merge sorting is a typical application of Divide and Conquer.
The ordered subsequences are combined to get the completely ordered sequences;
That is to say, first make each subsequence orderly, and then make subsequence segments orderly.
If two ordered tables are combined into one ordered table, it is called two-way merge.

def merge_sort(list):
	if len(list)<2: return list#Return a single element to the merge list
    mid=len(list)//2
    left=list[0:mid]#Left list
    right=list[mid:]#Right list
    return merge(merge_sort(left),merge_sort(right))
    #After dividing the left and right lists, the merged sequential tables will be returned to the previous level for merging

def merge(left,right):
    """
    //Merge sort merge two sequential tables into one list
    :param left: Sequence table on the left
    :param right: Sequence table on the right
    :return: Combined ordered list
    """
    finish=[]#Combined ordered list
    while left or right:#When at least one of two sequential tables is not empty
        if left and right:#When both sequential tables are not empty
            if left[0]<right[0]:#The left list element is smaller
                finish.append(left.pop(0))
            else:#Right list elements are small or equal
                finish.append(right.pop(0))
        elif left and not right:#Right list space
            finish +=left
            break
        elif not left and right:#Left column surface empty
            finish +=right
            break
    return finish#Return the merged list

6. Quick sorting

In essence, fast sorting is also the application of divide and conquer,
Select a reference value, and put the larger one in the array on the right,
Smaller than the reference value is placed on the left side of the list,
Then recursively use the above steps to the left and right of this list to get an ordered list.

(1) Method 1: digging and filling

This method is equivalent to the idea of using pointer, which is tedious, but the space complexity is low

def quick_sort(list):
	return qsort(list, 0, len(list) - 1)
    #List to be sorted, starting position and ending position

def qsort(list, start, end):
    if start < end:
        left = start
        right = end
        key = list[start]#First take out a reference value
    else:
        return list#Prove to have reached the minimum, just return to the list
    while left < right:#If the left and right end elements do not meet, it proves that a round of sorting is not over
        while left < right and list[right] >= key:#Compare with the reference value from the tail first
            right -= 1#Move the right pointer to the left
        if left < right:
            # The reason for breaking the while loop is that list [right] < = key
            #To avoid destroying the outer while loop in the previous loop, add this if
            list[left] = list[right]
            #Give the right value to the left, and the left initial value has been paid to the key as the reference value. Do not worry about data loss
            left += 1#Left lateral shift
        while left < right and list[left] < key:#Compare from head to reference
            left += 1#Left lateral shift
        if left < right:
            # To avoid destroying the outer while loop in the previous loop, add this if
            # Explain that the reason for breaking the while loop is list [left] > = key
            list[right] = list[left]#Left value to right pointer
            right -= 1#Shift right value left
    list[left] = key  # At this time, left=right, fill the pit with key
    qsort(list, start, left - 1)#Use recursion for left and right lists
    qsort(list, left + 1, end)
    return list

(2) Method 2

This method has a small amount of code, is easy to understand, and is very Python, but has a high space complexity

def quickSort1(list):
	    if len(list)<2:
        return list
    left=[];right=[]#Left and right empty array
    key=list.pop()#Reference value
    """
    //I thought about writing key=list[0], but the program crashed. After thinking about it, I found that,
    //If you choose not to pop up the first element, the following code will always put it at the beginning,
    //Then the subsequent recursion will not get the answer
    """
    for i in list:#Loop this list to group
        if i>key:#Greater than base, added to right array
            right.append(i)
        else:#Otherwise add to left array
            left.append(i)
    #Call left and right arrays recursively, and finally merge them to return
    return quickSort1(left)+[key]+quickSort1(right)

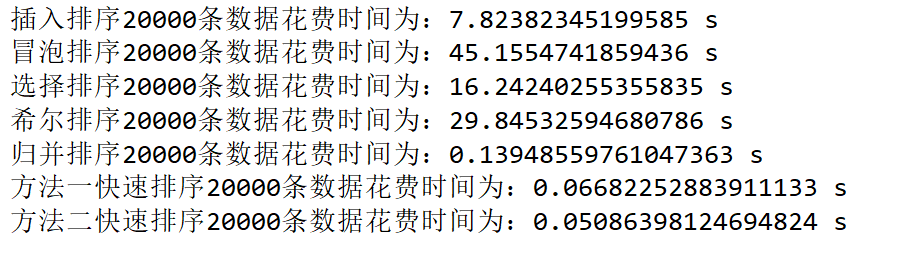
100000 data sorting time test:

1. Sorting test function

def testnum(n,sort):
    """
    //Test sorting algorithm time
    :param sort: Sorting algorithm
    :param n:Sort array length
    :return: Sorting time
    """
    nums = list(range(n))#Generate number list
    random.shuffle(nums)#There will be sequence table disorder
    start=time.time()#Starting time
    sort(nums)#Sort
    end=time.time()#Sort end time
    return (end-start)#Return algorithm sort time

2. Test the main function

def main():
    n=20000#Length of sequence to be sorted
    print("Insertion sort%s Time spent on data:%s s" %(n,testnum(n,insert_sort)))
    print("Bubble sort%s Time spent on data:%s s" % (n, testnum(n, bubble_sort)))
    print("Selection sort%s Time spent on data:%s s" % (n, testnum(n, selection_sort)))
    print("Shell Sort%s Time spent on data:%s s" % (n, testnum(n, shell_sort)))
    print("Merge sort%s Time spent on data:%s s" % (n, testnum(n, merge_sort)))
    print("Method 1 quick sorting%s Time spent on data:%s s" % (n, testnum(n, quick_sort)))
    print("Method 2 quick sorting%s Time spent on data:%s s" % (n, testnum(n, quickSort1)))

The results are as follows:

Due to different machines, the results may be different

Reprint please indicate the source!