All data in a computer is stored in binary form. Bit operation is actually the direct operation of binary data in memory, so the speed of data processing is very fast. In practical programming, if you can skillfully use bit operation, you can achieve the effect of four or two sets of kilograms. Because of these advantages of bit operation, bit operation has always been a hot issue in the written interview of major IT companies.

Bit Operating Basis

The basic bit operators are AND, OR, XOR, REVERSE, LEFT AND RIGHT. Their operation rules are as follows: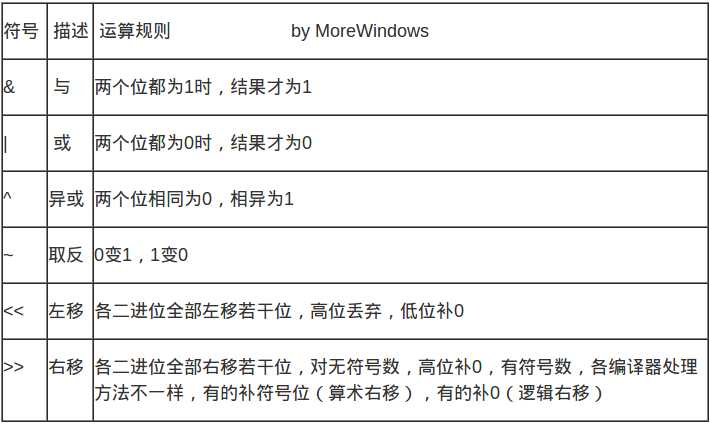Attention should be paid to the following points:

1. Among the six operators, only the ~inversion is a monocular operator, and the other five are binocular operators.
2. Bit manipulation can only be used for shaping data. Bit manipulation of float and double types can be erroneous by the compiler.
3. Operational priority of bit operators is relatively low, because brackets are used to ensure the order of operations as much as possible, otherwise the results are likely to be obscure. For example, we need to get numbers like 1, 3, 5, 9 that are 2^i+1. Written as int a = 1 << i + 1; is not correct, the program will first perform i + 1, then perform the left shift operation. It should be written as int a = 1 << i) + 1;
4. In addition, there are some compound operators, such as &=, |=, ^=, <=, >=.

package com.king.bit;

/**
 * @author taomk
 * @version 1.0
 * @since 15-5-10 2:23 p.m.
 */
public class BitMain {

    public static void main(String [] args) {
        int a = -15, b = 15;
        System.out.println(a >> 2); // - 4:-15 = 1111 0001 (binary), shifted to the right, the highest bit filled by the symbol bit will get 1111 1100, i.e. -4.
        System.out.println(b >> 2); // 3:15 = 0000 1111 (binary), right shift binary, the highest bit filled by symbol bit will get 0000 0011, that is, 3
    }
}

Common Bit Operating Skills

Here is a summary of some common applications of bitwise operations, such as judging parity, exchanging binary numbers, transforming symbols and finding absolute values. These tips are easy to remember and should be mastered skillfully.

Judgement parity

As long as the last bit is 0 or 1, 0 is an even number and 1 is an odd number. So if ((a & 1) == 0) can be used instead of if ((a%) 2 = 0) to judge whether a is even. The following program will output all even numbers between 0 and 100:

    for (int i = 0; i < 100; i ++) {
        if ((i & 1) == 0) { // Even numbers
            System.out.println(i);
        }
    }

Swap two numbers

int c = 1, d = 2;
c ^= d;
d ^= c;
c ^= d;
System.out.println("c=" + c);
System.out.println("d=" + d);

It can be understood as follows: the first step is a^=b that is a=(a^b); the second step is b^=a that is b=b^(a^b), because the ^ operation satisfies the commutation law, b^(a^b)=b^b^a. Because a number and its own exclusive or result are zero and any number and zero exclusive or will remain unchanged, B is assigned the value of a at this time; the third step, a^=b, is a=a^b, because the first two steps can be known as a=(a^b), b=a, so a=a^b means a=(a^b)^a. So A is assigned the value of B.

Transform symbol

The sign of transformation is that a positive number becomes a negative number and a negative number becomes a positive number. For - 11 and 11, the following transformation method can be used to convert - 11 to 11

1111 0101 (binary) - reverse - > 0000 1010 (binary) - plus 1 - > 0000 1011 (binary)

The same can be done to turn 11 into -11.

0000 1011 (binary) - reverse - > 0000 0100 (binary) - plus 1 - > 1111 0101 (binary)

Therefore, the transformation symbols only need to take the inverse and add 1. The complete code is as follows:

int a = -15, b = 15;
System.out.println(~a + 1);
System.out.println(~b + 1);

Absolute value

Bit operations can also be used to find absolute values. For negative numbers, positive numbers can be obtained by adding 1 to the inverse. Right-6 can do this:

1111 1010 (binary) - reverse - > 0000 0101 (binary) - plus 1 - > 0000 0110 (binary)

To get 6.

So first shift to take the symbol bit, int i = a > > > 31; note that if a is positive, I equals 0, negative, I equals - 1. Then I is judged - if I equals zero, return directly. Otherwise, return to ~a+1. The complete code is as follows:

int i = a >> 31;
System.out.println(i == 0 ? a : (~a + 1));

Now let's analyse it again. For any number, XOR with 0 will remain unchanged, XOR with - 1 or 0xFFFFFFFF FFFFFF is equivalent to the opposite. Therefore, if a is different from i, then subtract I (because I is 0 or - 1, so subtracting I means either adding 0 or adding 1) can also get the absolute value. So you can optimize the above code:

int j = a >> 31;
System.out.println((a ^ j) - j);

Note that this method does not use any judgment expressions, and some pen interviews require it, so it is recommended that readers remember this method (^______________

Bit Operation and Space Compression

The sieving prime number method is not introduced in detail here. This paper focuses on the optimization of the prime table used in the sieving prime number method to reduce its space occupation. To compress the space occupancy of the prime table, bitwise operations can be used. The following is an example code for calculating prime numbers within 100 by sieving prime number method (Note 2):

// Print primes less than 100:
// (1) For each prime, its multiple must not be a prime;
// (2) There are many repeated visits, such as flag[10] visiting flag[2] and flag[5] once each.
int max = 100;
boolean[] flags = new boolean[max];
int [] primes = new int[max / 3 + 1];
int pi = 0;

for (int m = 2; m < max ; m ++) {
    if (!flags[m]) {
        primes[pi++] = m;
        for(int n = m; n < max; n += m) {
            flags[n] = true;
        }
    }
}

System.out.println(Arrays.toString(primes));

The results are as follows:

[2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 0, 0, 0, 0, 0, 0, 0, 0, 0]

In the above program, bool arrays are used as markers. Bool data takes up one byte (8 bits). Therefore, using bit operations to compress space occupancy will reduce space occupancy by seven-eighths.

Next, consider how to place 1 on the specified position in the array. First, consider how to place 1 on the specified position for an integer. For an integer, the effect of putting 1 on a specified bit can be achieved by shifting 1 to the left and then phase with it. The code is as follows:

// Place 1 on a specified digit
int e = 0;
e |=  1 << 10;
System.out.println(e);

Similarly, it is possible to determine whether the specified bit is 0 or 1 by shifting 1 to the left and adding to the original number (or by shifting the original number to the right and then adding to 1).

//Determine whether the specified bit is 0 or 1
if ((e & (1 << 10)) != 0)
    System.out.println("1 on the specified bit");
else
    System.out.println("0 on the specified bit");

Extending to arrays, we can use this method, because arrays are also a continuous allocation of space in memory, it can be "considered" as a very long integer. Write a test code first to see how to use bit operations in arrays:

int[] bits = new int[40];
for (int m = 0; m < 40; m += 3) {
    bits[m / 32] |= (1 << (m % 32));
}
// Output the entire bits
for (int m = 0; m < 40; m++) {
    if (((bits[m / 32] >> (m % 32)) & 1) != 0)
        System.out.print('1');
    else
        System.out.print('0');
}

The results are as follows:

1001001001001001001001001001001001001001

You can see that every three arrays are set to 1, which proves that the way we operate on the arrays above is correct. Therefore, the above method of sieving prime number can be changed to the method of sieving prime number compressed by bit operation:

int[] flags2 = new int[max / 32 + 1];
pi = 0;
for (int m = 2; m < max ; m ++) {
    if ((((flags2[m / 32] >> (m % 32)) & 1) == 0)) {
        primes[pi++] = m;
        for(int n = m; n < max; n += m) {
            flags2[n / 32] |= (1 << (n % 32));
        }
    }
}

System.out.println();
System.out.println(Arrays.toString(primes));

The results are as follows:

[2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 0, 0, 0, 0, 0, 0, 0, 0, 0]

Bit Operating Tool Class

package com.king.bit;

/**
 * Java Common methods of bit operation encapsulate < br >
 */
public class BitUtils {

    /**
     * Gets the value < br > at the specified position of the arithmetic number
     * For example, 0000 1011 obtains a value of 1 for its 0th place and 0 < br > for its 2nd place.
     * 
     * @param source
     *            Number to be calculated
     * @param pos
     *            Specified location (0<=pos<=7)
     * @return The value of the specified location (0 or 1)
     */
    public static byte getBitValue(byte source, int pos) {
        return (byte) ((source >> pos) & 1);
    }


    /**
     * Set the value at the specified position of the arithmetic number to the specified value < br>.
     * Example: 0000 1011 needs to be updated to 0000 1111, that is, the value of the second place needs to be set to 1 < br >
     * 
     * @param source
     *            Number to be calculated
     * @param pos
     *            Specified location (0<=pos<=7)
     * @param value
     *            Only values of 0, or 1, all values greater than 0 are treated as 1, and all values less than 0 are treated as 0.
     * 
     * @return Number of results after operation
     */
    public static byte setBitValue(byte source, int pos, byte value) {

        byte mask = (byte) (1 << pos);
        if (value > 0) {
            source |= mask;
        } else {
            source &= (~mask);
        }

        return source;
    }


    /**
     * Inverse the specified position of the arithmetic number < br >
     * Example: 0000 1011 designated the third place to take the opposite, the result was 0000 0011; designated the second place to take the opposite, the result was 0000 1111 < br >
     * 
     * @param source
     * 
     * @param pos
     *            Specified location (0<=pos<=7)
     * 
     * @return Number of results after operation
     */
    public static byte reverseBitValue(byte source, int pos) {
        byte mask = (byte) (1 << pos);
        return (byte) (source ^ mask);
    }


    /**
     * Check if the specified position of the operand is 1 < br >
     * 
     * @param source
     *            Number to be calculated
     * @param pos
     *            Specified location (0<=pos<=7)
     * @return true Represents a specified location value of 1, false represents a specified location value of 0
     */
    public static boolean checkBitValue(byte source, int pos) {

        source = (byte) (source >>> pos);

        return (source & 1) == 1;
    }

    /**
     * Test entry function < br >
     * 
     * @param args
     */
    public static void main(String[] args) {

        // Take decimal 11 (secondary 0000 1011) as an example
        byte source = 11;

        // Take the second bit value and output, the result should be 0000 1011
        for (byte i = 7; i >= 0; i--) {
            System.out.printf("%d ", getBitValue(source, i));
        }

        // Output position 6 as 1, resulting in 75 (0100 1011)
        System.out.println("\n" + setBitValue(source, 6, (byte) 1));

        // Put the sixth bit back and output, the result should be 75 (0100 1011)
        System.out.println(reverseBitValue(source, 6));

        // Check if No. 6 is 1 and the result should be false.
        System.out.println(checkBitValue(source, 6));

        // The output is 1 bit, and the result should be 0.13
        for (byte i = 0; i < 8; i++) {
            if (checkBitValue(source, i)) {
                System.out.printf("%d ", i);
            }
        }

    }
}

Class BitSet

BitSet class: The size can be changed dynamically, and the value is a bit set of true or false. Used to represent a set of boolean flags. This class implements a bit vector for on-demand growth. Each component of bit set has a boolean value. Bits of BitSet are indexed with non-negative integers. Each indexed bit can be tested, set, or cleared. One BitSet can be used to modify the contents of another BitSet through logical and, logical or and logical exclusive or operations. By default, the initial values for all bits in the set are false.

Each bit set has a current size, which is the number of bits in the space currently used by the bit set. Note that this size is related to the implementation of bit set, so it may vary depending on the implementation. The length of bit set is related to the logical length of bit set and is independent of implementation.

Unless otherwise specified, any method that passes null parameters to BitSet will result in NullPointerException. It is not safe for multiple threads to operate a BitSet without external synchronization.

Constructor: BitSet() or BitSet(int nbits), the default initial size is 64.

public void set(int pos): The position POS is set to true. public void set (int bit index, Boolean value): Sets the bit at the specified index to the specified value. public void clear(int pos): The position POS is set to false. public void clear(): Set all bits in this BitSet to false. public int cardinality(): Returns the number of digits set to true in this BitSet. public boolean get(int pos): The return position is the word value of POS. public void and(BitSet other): Other operates with the BitSet and the result is a new value of the bitset. public void or(BitSet other): Other performs or operates on the set of bits, resulting in a new value for the set of bits. public void xor(BitSet other): Other operates exclusively or with the bitset, resulting in a new value for the bitset. Public void and Not (BitSet set): Clear all bits in this BitSet, set - BitSet public used to shield this BitSet int size(): Returns the number of bits in the actual space used when this BitSet represents the bit value. public int length(): Returns the "logical size" of this BitSet: the index of the highest set bit in the BitSet plus 1. public int hashCode(): Returns the set Hash code, which is related to the bit values in the set. public boolean equals(Object other): If the word in other is the same as the word in the set, return true. public Object clone(): Clone this BitSet and generate a new BitSet equivalent to it. Public String to String (): Returns the string representation of this bit set.

Example 1: Indicate which characters are used in a string

package com.king.bit;

import java.util.BitSet;

public class WhichChars {

    private BitSet used = new BitSet();

    public WhichChars(String str) {
        for (int i = 0; i < str.length(); i++)
            used.set(str.charAt(i));  // set bit for char
    }

    public String toString() {
        String desc = "[";
        int size = used.size();
        for (int i = 0; i < size; i++) {
            if (used.get(i))
                desc += (char) i;
        }
        return desc + "]";
    }

    public static void main(String args[]) {
        WhichChars w = new WhichChars("How do you do");
        System.out.println(w);
    }

Example 2:

package com.king.bit;

import java.util.BitSet;

public class MainTestThree {

    /**
     * @param args
     */
    public static void main(String[] args) {
        BitSet bm = new BitSet();
        System.out.println(bm.isEmpty() + "--" + bm.size());
        bm.set(0);
        System.out.println(bm.isEmpty() + "--" + bm.size());
        bm.set(1);
        System.out.println(bm.isEmpty() + "--" + bm.size());
        System.out.println(bm.get(65));
        System.out.println(bm.isEmpty() + "--" + bm.size());
        bm.set(65);
        System.out.println(bm.isEmpty() + "--" + bm.size());
    }

}

Example 3:

package com.king.bit;

import java.util.BitSet;

public class MainTestFour {

    /**
     * @param args
     */
    public static void main(String[] args) {
        BitSet bm1 = new BitSet(7);
        System.out.println(bm1.isEmpty() + "--" + bm1.size());

        BitSet bm2 = new BitSet(63);
        System.out.println(bm2.isEmpty() + "--" + bm2.size());

        BitSet bm3 = new BitSet(65);
        System.out.println(bm3.isEmpty() + "--" + bm3.size());

        BitSet bm4 = new BitSet(111);
        System.out.println(bm4.isEmpty() + "--" + bm4.size());
    }

Bit manipulation skills

// 1. Get the maximum of int type
System.out.println((1 << 31) - 1);// 2147483647, parentheses cannot be omitted due to priority
System.out.println(~(1 << 31));// 2147483647

// 2. Get the minimum of int type
System.out.println(1 << 31);
System.out.println(1 << -1);

// 3. Get the maximum of long type
System.out.println(((long)1 << 127) - 1);

// 4. Multiply by 2
System.out.println(10<<1);

// 5. Divide by 2 (Negative odd numbers are not available)
System.out.println(10>>1);

// 6. Multiply 2 to the m power
System.out.println(10<<2);

// 7. Divided by the m power of 2
System.out.println(16>>2);

// 8. Judging the Parity of a Number
System.out.println((10 & 1) == 1);
System.out.println((9 & 1) == 1);

// 9. Exchange two numbers without temporary variables.
a ^= b;
b ^= a;
a ^= b;

// 10. Take absolute values (on some machines, efficiency is higher than n > 0? N:-n)
int n = -1;
System.out.println((n ^ (n >> 31)) - (n >> 31));
/* n>>31 If n is positive, n > 31 equals 0, and N > 31 equals - 1 if n is negative.
If n is positive n^0-0 and N is negative n^-1, the complements of N and - 1 need to be calculated, XOR and then the complements.
The result is that n changes sign and absolute value minus 1, and minus - 1 is absolute value. */

// 11. Take the maximum of two numbers (on some machines, efficiency is higher than a > b? A: b)
System.out.println(b&((a-b)>>31) | a&(~(a-b)>>31));

// 12. Take the minimum of two numbers (on some machines, efficiency is higher than a > b? B: a)
System.out.println(a&((a-b)>>31) | b&(~(a-b)>>31));

// 13. Determine whether the symbols are the same (true means that x and y have the same symbols, false means that x and y have the opposite symbols. )
System.out.println((a ^ b) > 0);

// 14. Calculate the n-th power of 2 n > 0
System.out.println(2<<(n-1));

// 15. Judge whether a number n is a power of 2?
System.out.println((n & (n - 1)) == 0);
/*If it is a power of 2, n must be 100... n-1 is 1111....
So the result of operation and calculation is 0.*/

// 16. Find the average of two integers
System.out.println((a+b) >> 1);

// 17. From low to high, take the m position of n
int m = 2;
System.out.println((n >> (m-1)) & 1);

// 18. From low to high. Position m of n at 1
System.out.println(n | (1<<(m-1)));
/*Move 1 left to m-1 to find the m-th position, and get 000... 1... 000
n Doing or calculating with this number*/

// 19. From low to high, the m position of n is 0.
System.out.println(n & ~(0<<(m-1)));
/* Move 1 left to m-1 to find the m-th position, and then turn it back to 111...0...1111.
n The operation and calculation of the sum number*/