I want to deepen my learning and understanding of DFS through the analysis of two DFS examples. If there are any mistakes, I will not hesitate to give advice.

1. combination

The combined topics are as follows: (the topic comes from codeup: ID:100000608, question B) slightly changed (removing non recursive requirements)
Permutation and combination are commonly used mathematical methods, in which combination is to extract r elements from n elements (regardless of order and R < = n). We can simply understand n elements as natural numbers 1, 2 , N, any number of R. For example, n = 5, r = 3, all combinations are:
1 2 3
1 2 4
1 2 5
1 3 4
1 3 5
1 4 5
2 3 4
2 3 5
2 4 5
3 4 5

#include<iostream>
using namespace std;
const int Max=100;
int n,r;
int num[Max]={0};
//When the boundary is reached, 
void DFS(int index,int count){
	//It doesn't mean much. It's just for better analysis
	cout<<"**"<<index<<" "<<count<<" "<<endl;
	//Record
	num[count]=index;
	//Boundary, when there are r elements, the boundary value is reached
	if(count==r){
		//From num[1]~num[r] is temporary data
		for(int i=1;i<=r;i++){
			cout<<num[i]<<" ";
		}
		cout<<endl;
		return;
	} 
	//The sum of all combinations starting with 1 ~ n-r is the desired combination
	//Starting from index+1~n 
	for(int i=index+1;i<=n;i++){
		DFS(i,count+1);
	}
}
int main(){
	cin>>n>>r;
	DFS(0,0);
	return 0;
}

The operation results after n=5 and r=3 are as follows: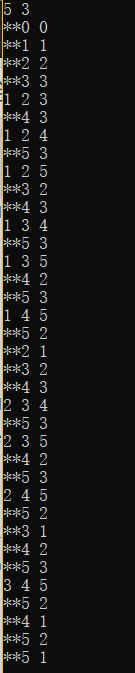

The flow chart is as follows: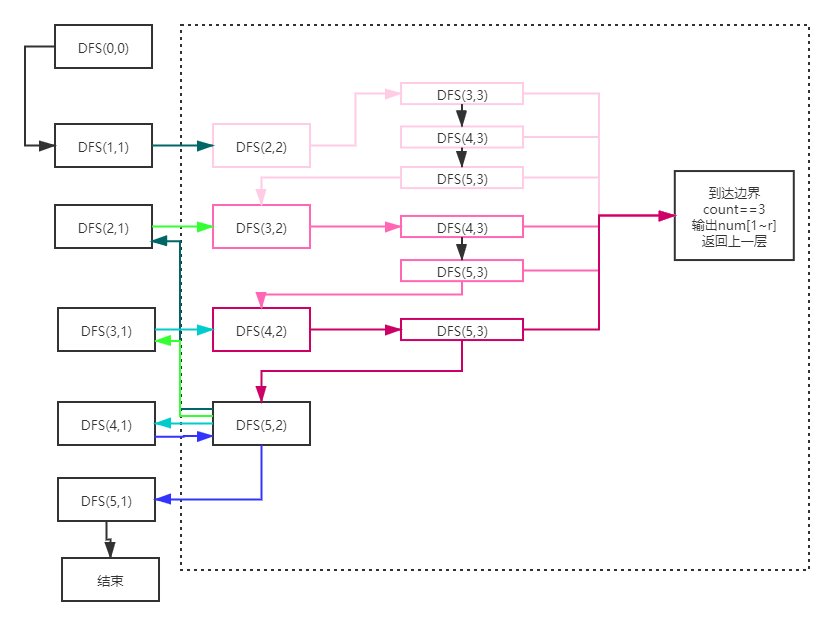

It can be seen from the above figure that when DFS(1,1) goes through the cycle in the virtual frame (that is, the dark blue arrow points to DFS(2,1) (that is, the dark blue arrow points to the virtual frame), then DFS(2,1) points to the virtual frame with the green arrow, goes through the process in the virtual frame, points out to DFS(3,1), and ends the cycle in DFS(5,1).
This corresponds to:

void DFS(int index,int count){
	//Code ellipsis
	...
	//The sum of all combinations starting with 1 ~ n-r is the desired combination
	//Starting from index+1~n 
	for(int i=index+1;i<=n;i++){
		DFS(i,count+1);
	}
}

When index=0, count=0, there are 5 DFS(1,1), DFS(2,1), DFS(3,1), DFS(4,1), DFS(5,1) in the outermost layer.

Then it goes into the inner recursion of DFS(1,1), goes through the flow in the virtual frame, and returns to DFS(2,1), until DFS(5,1), and finally ends.

void DFS(int index,int count){
	//It doesn't mean much. It's just for better analysis
	cout<<"**"<<index<<" "<<count<<" "<<endl;
	//Record
	num[count]=index;
	//Boundary, when there are r elements, the boundary value is reached
	if(count==r){
		//From num[1]~num[r] is temporary data
		for(int i=1;i<=r;i++){
			cout<<num[i]<<" ";
		}
		cout<<endl;
		return;
	} 
	//Code ellipsis
	...
}

Because every recursion will save the data currently accessed, count is the position of the current index in the num array. When the recursion boundary is reached, the extracted element count has reached the r=3 required by the topic. The required content already exists in the num array, and the output is OK.

2. complete sorting

Title: (abbreviated expression) input n (positive integer less than 21), and give the full permutation of 1~n

#include<cstdio>
using namespace std;
const int Max=11;
int n;
//Store sort elements 
int per[Max]={0};
//Mark whether the corresponding element has participated in sorting, true has participated, false has not participated 
bool hashTable[Max]={false};
//Recursive implementation of DFS 
void DFS(int index){
	//If the number of participants reaches n, the boundary is reached 
	if(index==n+1){
		//Output it 
		for(int i=1;i<=n;i++){
			if(i!= n){
				printf("%d ",per[i]);
			} else {
				printf("%d\n",per[i]);
				return;
			}
		}
	}
	//Total permutation of N numbers = sum of all permutations starting from 1 to n 
	for(int i=1;i<=n;i++){
		//Determine whether to participate in sorting 
		if(!hashTable[i]){
			//Store the elements currently participating in sorting to per 
			per[index]=i;
			//Set use flag to true 
			hashTable[i]=true;
			//Arrange next location 
			DFS(index+1);
			//Set the flag position of the current location element to false for the next round of use 
			hashTable[i]=false;
		}
	}
}
int main(){
	while(scanf("%d",&n)!=EOF){
		DFS(1);
	}
	return 0;
} 

The operation results are as follows: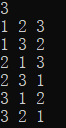

The operation flow chart is as follows: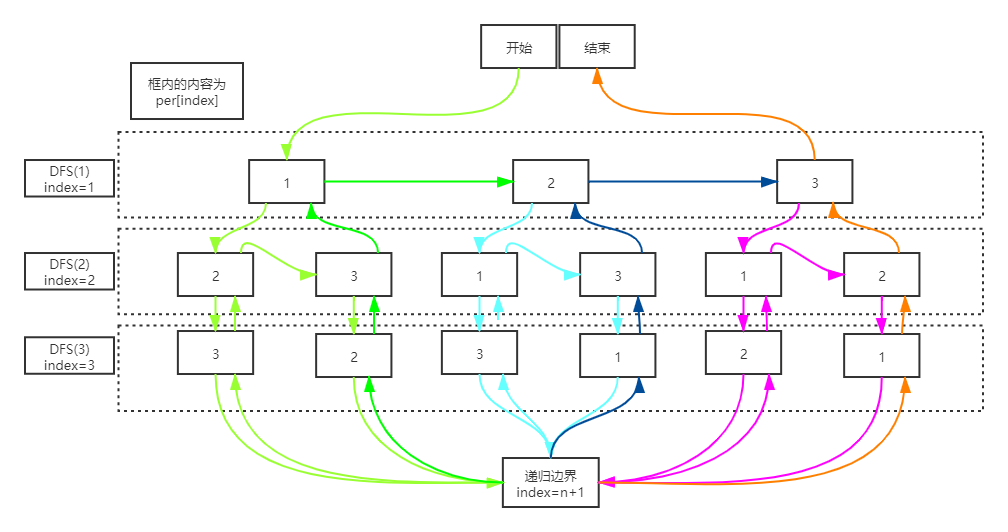

As can be seen from the above figure, starting from DFS(1)=1, what to recurse at this time is DFS(1) of the same layer = 2, DFS(1) = 3. Then DFS(1)=1 continues to recursively drill down to the DFS(2) layer. At this time, DFS(2)=2 or 3. Select DFS(2)=2 to enter the next layer. Only the last element of DFS(3) is optional, that is, DFS(3)=3. Then continue to the next layer. DFS(4) reaches the recursion boundary and outputs and returns.
For each layer returned, set the flag bit hashTable[i] of the element of the corresponding layer to false, so that the next recursion can continue. When DFS(2)=2 is selected, and since hashTable[3] has been set to false after being used in the upper layer of recursion, it can be used continuously. Therefore, DFS(2)=3, and then scan hashTable[1~n], and the corresponding flag bit of that element is false, which one should be used. Until the recursion boundary, and then return and false the corresponding flag position. When returning to DFS(1)=1, enter the recursion of DFS(1)=2, and hashTable[1]=false.
The recursion process of DFS (1 = 2) is similar to that of DFS (1 = 1), which will not be discussed in detail.

3. Summary

In the last two questions, let's say that there is such an array num[1~n], fill n numbers into the num array. In total sorting, num[1] can fill n elements, num[2] can fill n-1 elements, num[3] can fill n-2 elements num[n] can be filled with one element.
The difference between the above two questions is whether the previously used elements can be reused. A sign digit group hashTable[Max] is added to the full sorting to indicate the use of elements. Each recursion scans 1~ n, and the previous elements can be used. The combination is that every time you recursively select from the current index+1~ n, you can only select from a sequence of elements larger than the current one.
Possible templates for DFS:

//Specific parameters need to be analyzed
//index indicates element number
//Other indicates possible other parameters
void DFS(int index,{int other}){
	//If the recursion boundary is reached
	if(Recursive boundary){
		//Output content
	}
	//Enter next recursion
	//The branch road is the road to the next floor
	DFS(index+1,{other});
}