Catalog
A - Casimir's String Solitaire
C - Ticks (Violence + Thinking)
D - Productive Meeting (Greed + Thinking + Priority Queue)
E1.Permutation Minimization by Deque
E2.Array Optimization by Deque (Greedy+Discrete+Tree Array)
A - Casimir's String Solitaire
Topic:
Gives a string consisting of only the letters A, B and C. A and B cancel out, B and C cancel out.
Ask if you can get an empty string.
Ideas:
Count the number of A,B,C characters to determine if B equals A+C
AC code: omitted
B - Shifting Sort (Violence)
Topic:
Given a number sequence of length n, the sequence is ordered by a rule, and the number of output operations and the way of operation for each operation does not require a minimum number of operations. Rule: Select an interval [l,r], and move the number of operations left by d units.
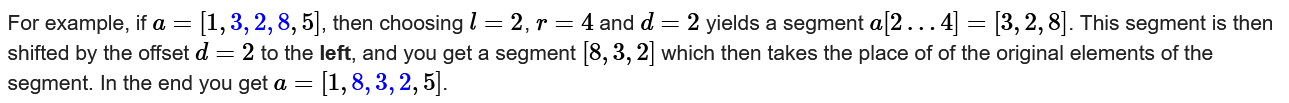
Ideas:
Array ordering means that each last number has its own place, traversing through n locations, each time finding the correct number of I locations. Select the smallest one i n the interval i~n and the next one i n the interval i+1~n to determine the number of i+1 locations. Each offset d = the subscript-i of the correct number (the starting subscript of the query minimum value interval).
Reason for WA: Fixed offset of 1 at a time, move step by step, move too many times.
AC code:
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxx=1e5+10;
vector<int>a;
int c[60];
struct node
{
int l,r,d;
}w[1000];
int main()
{
int t,n,x;
cin>>t;
while(t--)
{
cin>>n;
a.clear();
for(int i=1;i<=n;i++)
{
cin>>x;
a.push_back(x);
}
for(int i=0;i<n;i++)
{
w[i].l=0;
w[i].r=0;
w[i].d=0;
}
// sort(c+1,c+1+n);
int p=0;
int cnt=0;
int id=0;
int k=0;
int tt;
while(p<n)
{
int minn=INT_MAX;
for(int i=p;i<n;i++)
{
if(minn>a[i])
{
minn=a[i];
id=i;
}
}
if(id>p)
{
w[k].l=p+1;
w[k].r=id+1;
w[k].d=id-p;
tt=a[id];
a.erase(a.begin()+id);
a.insert(a.begin()+p,tt);
k++;
p++;
}
else
{
p++;
//continue;
}
}
cout<<k<<endl;
for(int i=0;i<k;i++)
{
cout<<w[i].l<<" "<<w[i].r<<" "<<w[i].d<<endl;
}
}
}C - Ticks (Violence + Thinking)
Topic:
Gives a character matrix of n*m to determine whether the * of the matrix is used to form a V-shape of at least k.
In the second example, you could have a V of size 2 and a V of size 3.
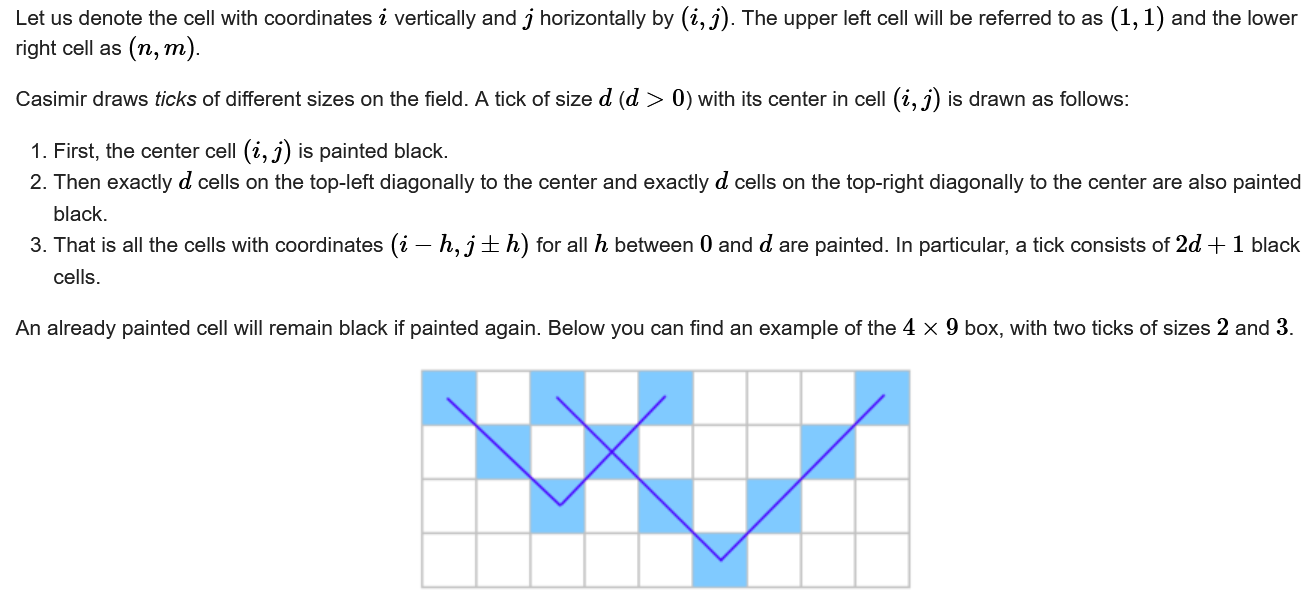
Ideas:
Violence, for each * to make it the bottom of the V type, determines if its d is greater than k, if greater then marks each point of the V type, and finally determines if the marked points are equal to the total number of *.
AC code:
#include<bits/stdc++.h>
using namespace std;
char a[30][30];
int vis[30][30];
int t,n,m,k;
void check(int x,int y)
{
int d=0,c=0;
for(int i=x-1;i>=1;i--)
{
c++;
if((y-c)<0||(y+c)>m)
break;
if(a[i][y-c]=='*'&&a[i][y+c]=='*')
{
d++;
//continue;
}
else
{
break;
}
}
if(d>=k)
{
vis[x][y]=1;
for(int i=1;i<=d;i++)
{
vis[x-i][y+i]=1;
vis[x-i][y-i]=1;
}
}
}
int main()
{
cin>>t;
while(t--)
{
cin>>n>>m>>k;
int sum=0;
int s=0;
bool f;
memset(vis,0,sizeof(vis));
for(int i=1; i<=n; i++)
{
for(int j=1; j<=m; j++)
{
cin>>a[i][j];
}
}
for(int i=1; i<=n; i++)
{
for(int j=1; j<=m; j++)
{
if(a[i][j]=='*')
{
sum+=1;
check(i,j);
}
}
}
for(int i=1; i<=n; i++)
{
for(int j=1; j<=m; j++)
{
if(vis[i][j]==1)
{
s++;
}
}
}
if(sum==s)
cout<<"YES"<<endl;
else
cout<<"NO"<<endl;
}
}D - Productive Meeting (Greed + Thinking + Priority Queue)
Topic:
Given n n the number of n, choose two different numbers each, and subtract one from each of them, so that you can reduce as many operations as possible, and output the number of operations and their schemes.
Ideas:
A priority queue, a large root heap, takes two elements from the top of the heap at a time, the maximum and the secondary maximum, minus one each, and puts them back into the queue.
AC code:
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxx=2e5+10;
priority_queue<pair<int,int>> q;
pair<int,int>a[maxx];
pair<int,int>p[maxx];
int main()
{
int t,n;
cin>>t;
while(t--)
{
while(!q.empty())
q.pop();
cin>>n;
for(int i=1;i<=n;i++)
{
cin>>a[i].first;
a[i].second=i;
if(a[i].first>0)
{
q.push(a[i]);
}
}
int c=0;
pair<int,int>p1,p2;
while(q.size()>1)
{
p1=q.top();q.pop();
p2=q.top();q.pop();
p[c].first=p1.second;
p[c].second=p2.second;
c++;
if(--p1.first)
q.push(make_pair(p1.first,p1.second));
if(--p2.first)
q.push(make_pair(p2.first,p2.second));
}
cout<<c<<endl;
for(int i=0;i<c;i++)
{
if(p[i].first>p[i].second)
swap(p[i].first,p[i].second);
cout<<p[i].first<<" "<<p[i].second<<endl;
}
}
}E1.Permutation Minimization by Deque
Topic:
Given a sequence A with a length of n, there is an empty double-ended queue B where each element i n A is placed (1 to n) i n B i n turn. The first element of B is not greater than A[i], and A[i] is placed i n the first position of B, otherwise it is placed at the end. Output sequence B.
Ideas:
Dual-end queue + simulation, vector s simulation will time out.
AC code: omitted
E2.Array Optimization by Deque (Greedy+Discrete+Tree Array)
Topic:
Given a sequence A with a length of n, there is an empty double-ended queue B. Each element in A is placed in B in turn (1 to n).
That is, place A[i] at the first or last position of B and find out how many reverse pairs the reverse order has to the least sequence B.
Reverse order pair: if i<j, b[i]>b[j].
Ideas:
Local optimum guarantees global optimum. Each time an element is inserted, consider whether it is inserted before or after the current B, and select a position with fewer inverse pairs after insertion. Example: Current sequence B [2, 5, 3, 4], at which point there are [5, 3] [5, 4] inverse pairs;
If the element to be inserted is 3, insert the reverse order of the preceding [3, 2, 5, 3, 4] pair [3, 2] [5, 3] [5, 4];
When x is inserted after [2, 5, 3, 4, 3], the reverse order at this time is [5, 3] [5, 4] [5, 3] [4, 3].
The data is discretized, and inversion pairs only need to know how many elements are inserted larger than the current sequence B, that is, they only need to know the relative relationship between them, and a[i] has a larger range, (1e-9~1e9) so they can be discretized.
Data Discretization Template:
for(int i=1;i<=n;i++)
{
cin>>a[i];//Original Array
b.push_back(a[i]);
}
sort(b.begin(),b.end());
b.erase(unique(b.begin(),b.end()),b.end());//Duplicate removal
for(int i=1;i<=n;i++)
{
a[i]=lower_bound(b.begin(),b.end(),a[i])-b.begin()+1;
}//After weighting, rank b[i] from smallest to largest and assign a[i]Tree Array Dynamic Maintenance (Single-point Update Query Template Title)
When a[i] is first: sum(a[i]-1): Number of queries ranked less than a[i]-1
When a[i] is placed behind: sum(n)-sum(a[i]): number greater than a[i]===total number-number less than a[i]
for(int i=1;i<=n;i++)
{
tmp=a[i];
add(tmp,1);
p1=sum(tmp-1);//Add a[i] before
p2=sum(n)-sum(tmp);//Add a[i] after
ans+=min(p1,p2);
}
AC code:
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxx=2e5+50;
ll n;
ll a[maxx];
ll tr[maxx];
ll lowbit(ll x)
{
return x&-x;
}
void add(ll x,ll c)
{
while(x<=n)
{
tr[x]+=c;
x+=lowbit(x);
}
}
ll sum(ll x)
{
ll res=0 ;
while(x>=1)
{
res+=tr[x];
x-=lowbit(x);
}
return res;
}
int main()
{
int t;
cin>>t;
while(t--)
{
cin>>n;
vector<ll>b;
for(int i=1;i<=n;i++)
{
cin>>a[i];
b.push_back(a[i]);
}
sort(b.begin(),b.end());
b.erase(unique(b.begin(),b.end()),b.end());
for(int i=1;i<=n;i++)
{
a[i]=lower_bound(b.begin(),b.end(),a[i])-b.begin()+1;
}
memset(tr,0,sizeof(tr));
ll ans=0;
ll tmp,p1,p2;
for(int i=1;i<=n;i++)
{
tmp=a[i];
add(tmp,1);
p1=sum(tmp-1);//Add before
p2=sum(n)-sum(tmp);//After
ans+=min(p1,p2);
}
cout<<ans<<endl;
}
return 0;
}