Competition link: Click here to transfer

Link to official solution: Click here to transfer

1573A Countdown topic link: Click here to transfer

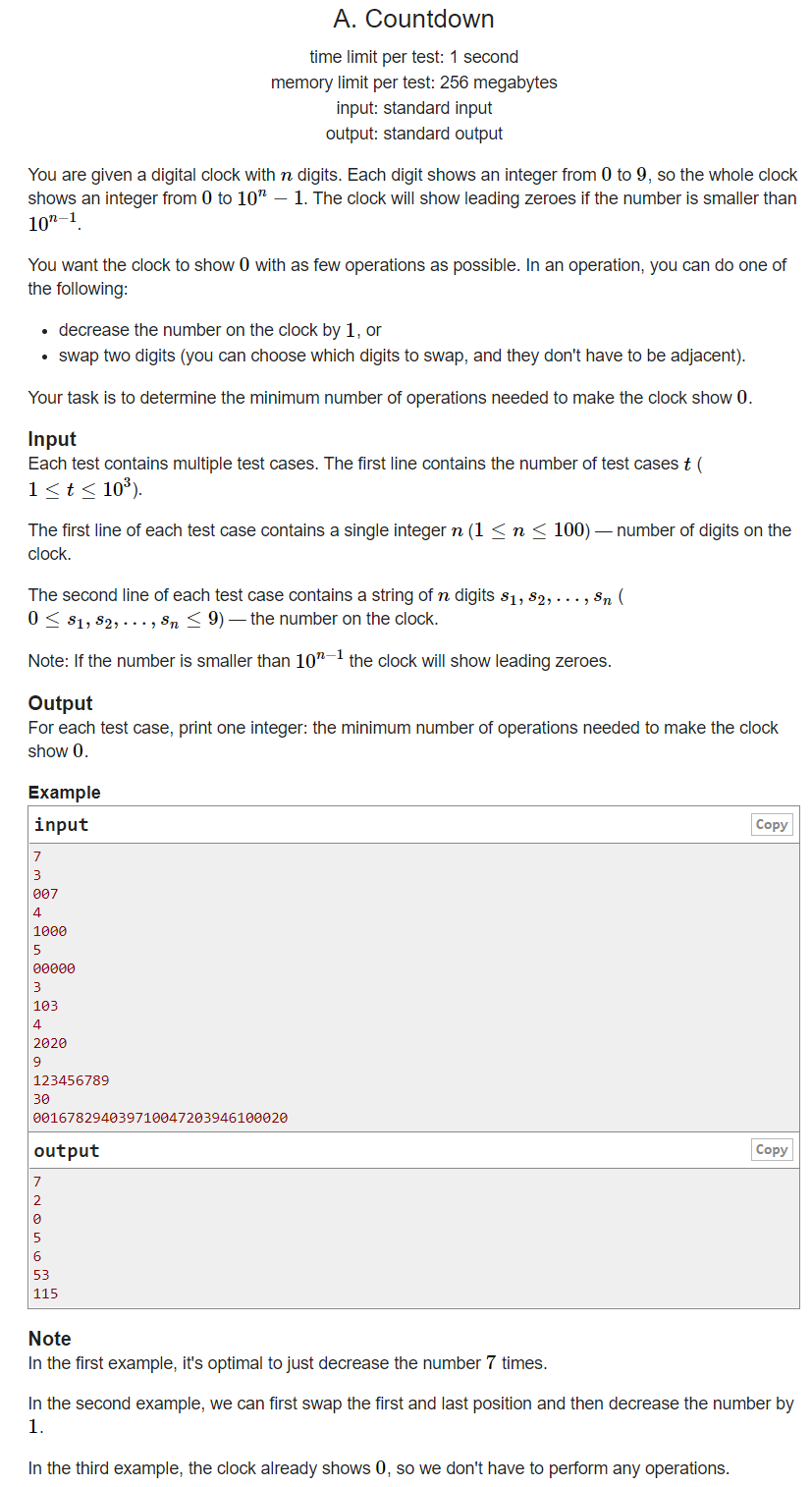Meaning:
There is a sequence, you have to change it all into 0. You can perform the following two operations to exchange elements in two positions, which is the last element minus one. Find the minimum number of operations required to complete
Idea:
If there is a leading zero, first find the first position that is not 0. Then simulate the next digital, including the last bit and not the last bit, and 0 and non-0.

#include<bits/stdc++.h>
using namespace std;
string s;
int t, n;

int main()
{
	ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);
	cin >> t;
	while (t--)
	{
		cin >> n>>s;
		int flag = 0;
		int ans = 0;
		int pos = 0;
		for (int i = 0; i < s.length(); i++)
		{
			if (s[i] != '0')
			{
				pos = i;
				flag = 1;
				break;
			}
		}
		if (flag == 0)
		{
			cout << 0 << endl;
			continue;
		}
		for (int i = pos; i < s.length(); i++)
		{
			int temp = s[i] - '0';
			if (i == s.length() - 1) ans += temp;
			else if(i!=s.length()-1&&temp!=0)ans += (temp + 1);
		}
		cout << ans << endl;
	}
	return 0;
}

1573B Swaps title link: Click here to transfer

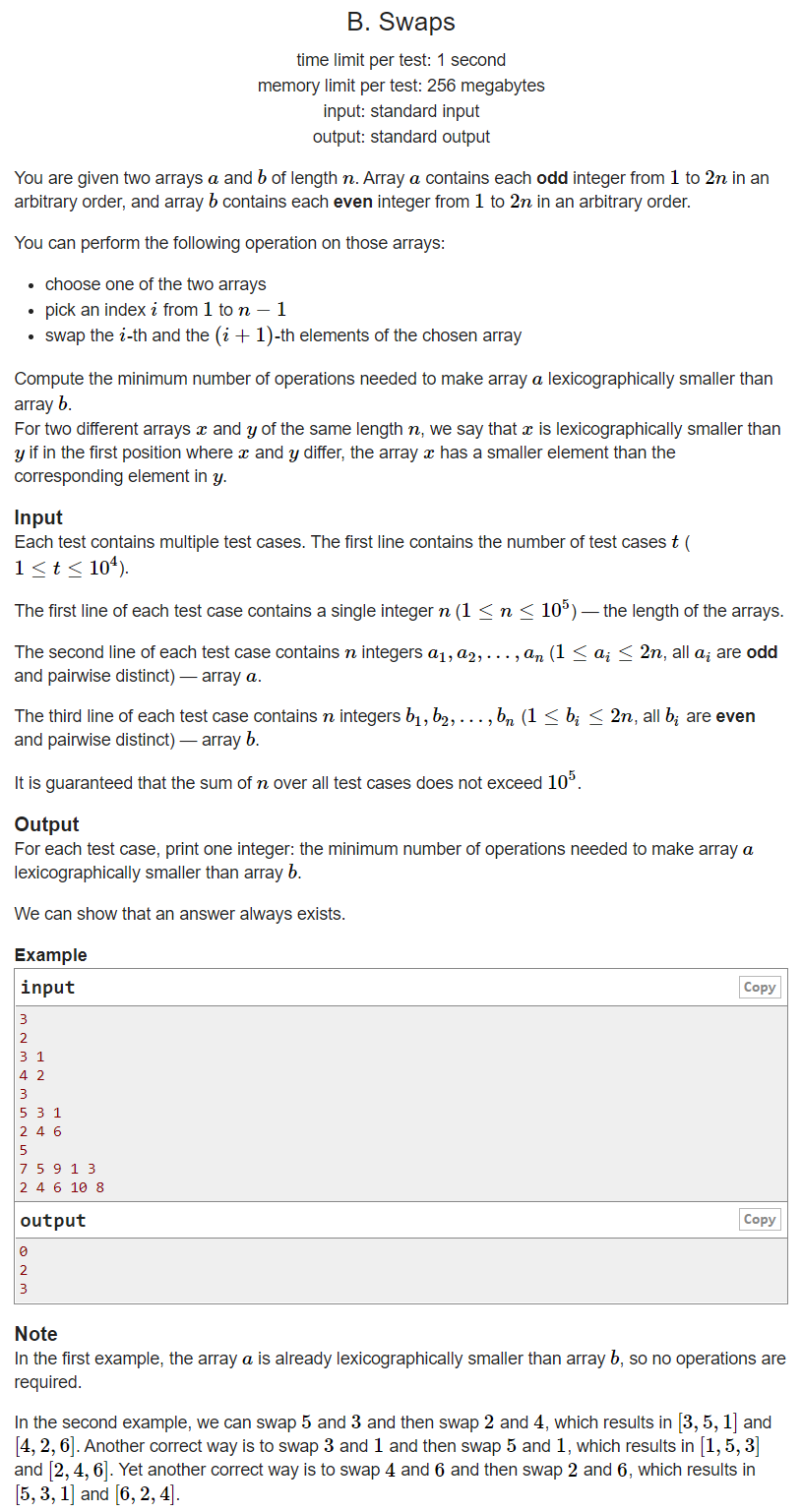Meaning:
a array is [ 1 , 2 n ] \left[1,2n\right] Any arrangement of all odd numbers in [1,2n], b array is [ 1 , 2 n ] \left[1,2n\right] Any arrangement of all even numbers in [1,2n]. You can select any element of an a or b array to be interchanged with its left and right elements. If the dictionary order of array A is less than that of array b, it needs at least several operations.
Idea:
Because of different parity, dictionary order comparison only needs to look at the first place.
For any element of the a array, to make it a 1 a_1 a1, you need to find the first one in the b array that is greater than a i a_i The element of ai ， whose position is j. The number of operations required is i+j-2
So the time complexity is o( n 2 n^2 n2), definitely not.
Let's replace the a array with 1,3,5,7,..., 2n-3,2n-1. In this way, if an element in b is less than the odd number appearing in the increasing sequence, it must also be less than the current odd number, that is, you only need to scan the b array once, and there is no need to scan b from 1 every time.
Create a new pos array to record the position of the first even number greater than an odd number in b. Finally, it can be solved in the process of traversing the a array.

#include<bits/stdc++.h>
using namespace std;
#define MAXN 200005
int a[MAXN];
int b[MAXN];
int pos[2 * MAXN];
int n,t;
int main()
{
	ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);
	cin >> t;
	while (t--)
	{
		cin >> n;
		int ans = 99999999;
		for (int i = 1; i <= n; i++) cin >> a[i];
		for (int i = 1; i <= n; i++) cin >> b[i];
		for (int i = 1,j=1; i < 2 * n; i += 2)
		{
			while (b[j] < i) j++;
			pos[i] = j;
		}
		for (int i = 1; i <= n; i++) ans = min(ans, i + pos[a[i]] - 2);
		cout << ans << endl;
	}
	return 0;
}

1573C Book title link: Click here to transfer

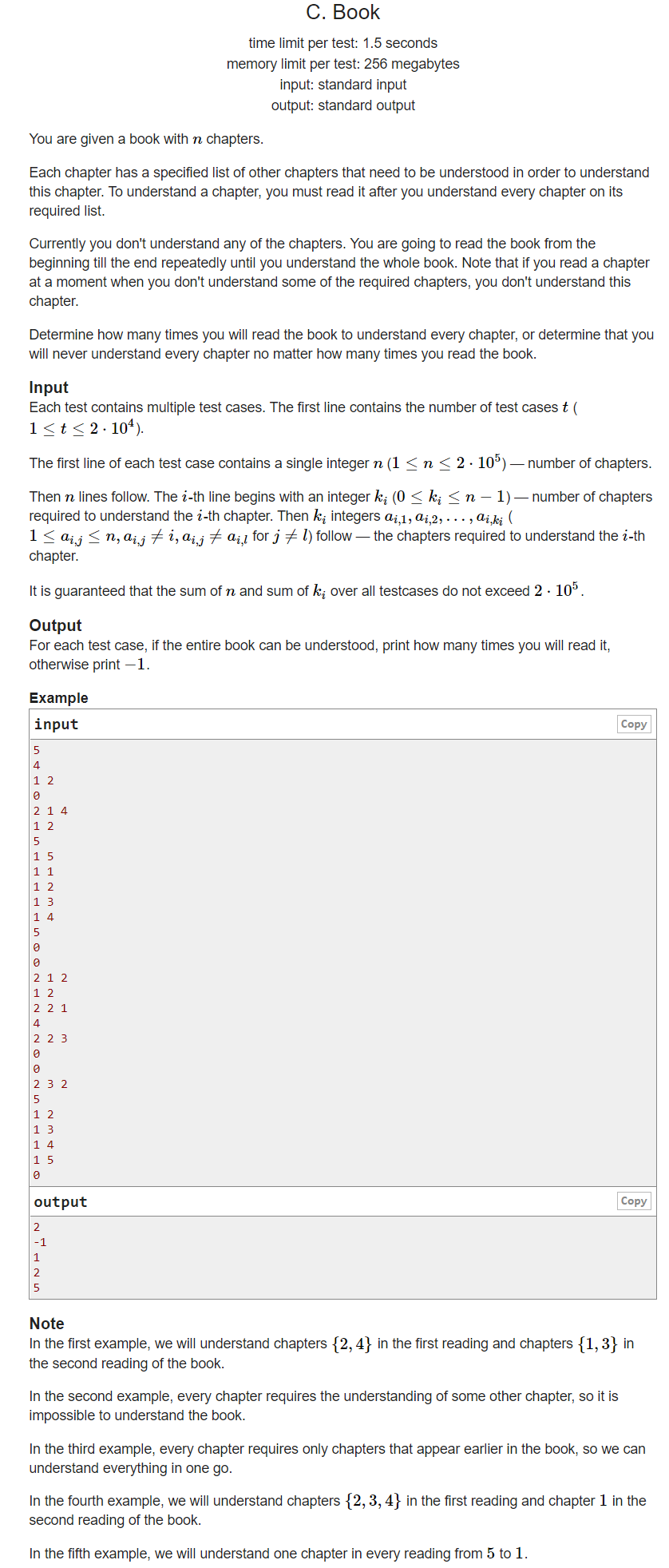
Meaning:
One book is badly edited. Only after reading some chapters can you understand a chapter. Define those chapters as the preceding chapters. You must read all the preceding chapters before you can understand the current chapter. You can't understand the current chapter if you haven't read or haven't read it. Now someone wants to fully understand the book. He will read each chapter in order to judge whether he can fully understand the book. If he can output the total number of reading rounds.
Idea:
Very naked topology. Join those chapters that can be understood without the preceding chapters, corresponding to the penetration of their subsequent chapters - 1. If the penetration of some subsequent chapters becomes 0, they will also join the team.

• If the sequence number of the subsequent chapter j is greater than that of the preceding chapter i, it can be its turn in this round
  t i m e s [ j ] = m a x ( t i m e s [ j ] , t i m e s [ i ] ) times\left[j\right]=max(times\left[j\right],times\left[i\right]) times[j]=max(times[j],times[i])

• If the sequence number of the subsequent chapter j is less than that of the preceding chapter i, it cannot be its turn in this round
  t i m e s [ j ] = m a x ( t i m e s [ j ] , t i m e s [ i ] + 1 ) times\left[j\right]=max(times\left[j\right],times\left[i\right]+1) times[j]=max(times[j],times[i]+1)

  It should be noted that this process must be performed every time the penetration minus 1, not only when the penetration equals 0. The number of rounds of the last preceding chapter that needs to be understood is not necessarily the largest.
  Suppose you understand a certain Chapter X, corresponding to the preceding chapters a and b that can understand y. it happens that the sequence number of a is less than x, and the sequence number of b is greater than x. in the traversal process, a may come earlier than b, and b becomes the last preceding chapter you think you need to understand. In fact, a is the last preceding chapter you need to understand, and the program will produce an error.
  In other words, a penetration of 0 means that the conditions for understanding this chapter have been completed, and this chapter can not be understood in the current number of rounds. If you still don't understand, replacing part of the code with may deepen your understanding
  This is a false code:

for (auto i:v[x])
			{
				indgr[i]--;
				if (indgr[i] == 0)//Because I understand x, I can understand y
				{
					cnt++;				
					if (x > i) times[i] = max(times[i],times[x]+1);//It's time for the next one
					else if (x < i) times[i]=max(times[i],times[x]) ;//You can still see y in this round
					q.push(i);
				}
			}

This is true Code:

#include<bits/stdc++.h>
using namespace std;
#define MAXN 200005
#define ll long long
int t, n;
vector <int> v[MAXN];//Post section of i
int indgr[MAXN];
int times[MAXN];
int main()
{
	ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);
	cin >> t;
	while (t--)
	{
		cin >> n;
		for (int i = 1; i <= n; i++)
		{
			v[i].clear();
			indgr[i] = 0;
			times[i] = 0;
		}
		queue <int> q;
		int cnt = 0;//Number of books understood
		for (int i = 1; i <= n; i++)
		{
			int m, temp;
			cin >> m;
			indgr[i] = m;
			if (m == 0)
			{
				times[i] = 1;
				q.push(i);
				cnt++;
			}
			while (m--)
			{
				cin >> temp;//Understand temp before you can understand i
				v[temp].push_back(i);
			}
		}
		int ans = 0;//How many rounds did you watch
		while (!q.empty())
		{
			int x = q.front(); q.pop();
			//Cout < < now is < < x.val < < endl;
			for (auto i:v[x])
			{
				indgr[i]--;
				if (x > i) times[i] = max(times[i], times[x] + 1);//It's time for the next one
				else if (x < i) times[i] = max(times[i], times[x]);//You can still see y in this round
				if (indgr[i] == 0)//Because I understand x, I can understand y
				{
					cnt++;									
					q.push(i);
				}
			}
		}
		if (cnt != n) cout << -1 << endl;
		else
		{
			for (int i = 1; i <= n; i++) ans = max(ans, times[i]);
			cout << ans << endl;
		}
	}
	return 0;
}