Competition link: Click here to transfer
Link to official solution: Click here to transfer
1562A The Miracle and the Sleeper topic link: Click here to transfer
Meaning:
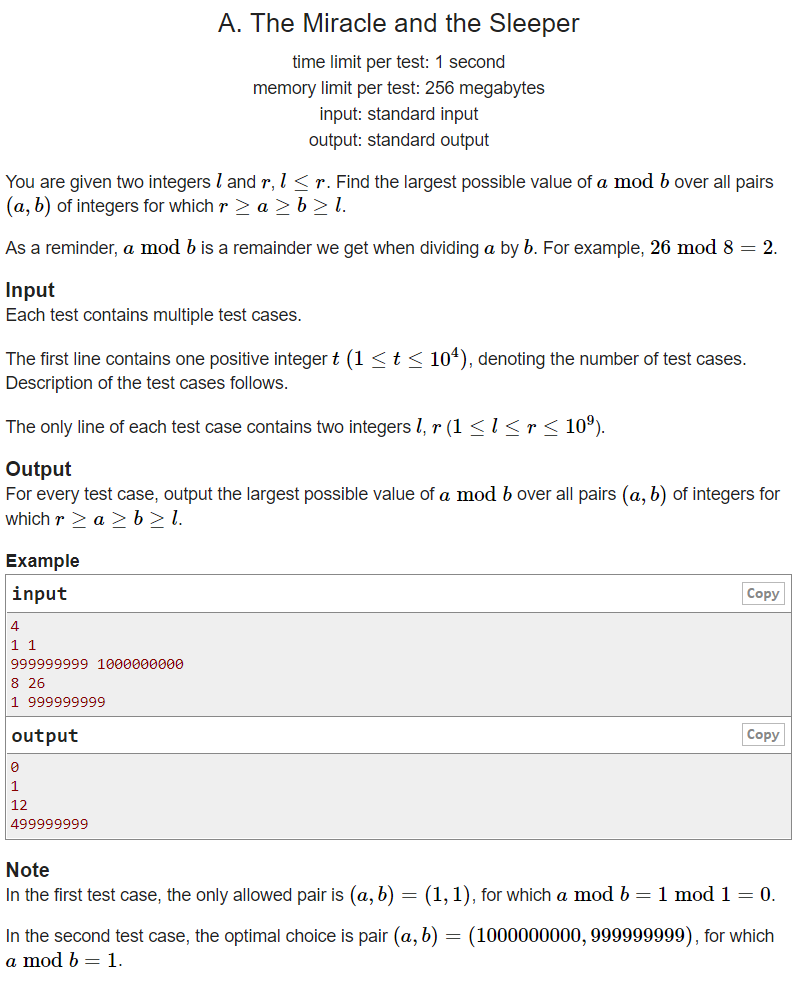
Given a range
[
l
,
r
]
\left[{l},{r}\right]
[l,r], arbitrarily select two numbers a and B within this range, so that b mod a is the largest
Idea:
If l > R / 2, output r-l directly. Otherwise, output (r-1)/2. Because theoretically, when the modulus is maximum, the divisor is 1, and the modulus is maximum (r-1)/2
#include<bits/stdc++.h>
using namespace std;
int t, a, b;
int main()
{
ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);
cin >> t;
while (t--)
{
cin >> a >> b;
cout << min(b - a, (b - 1) / 2) << endl;
}
return 0;
}
1562B Scenes From a Memory topic link: Click here to transfer
Meaning:
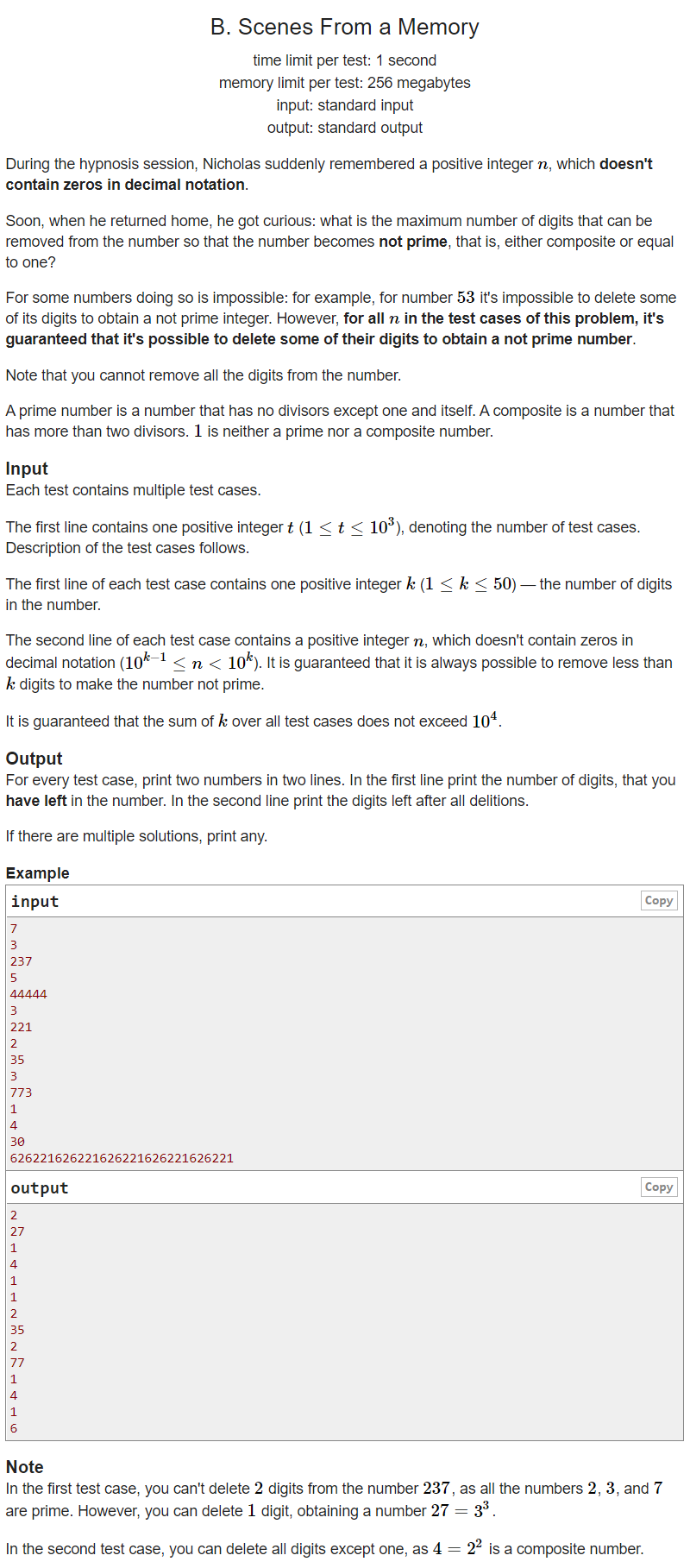
Given a number (excluding 0), you can delete any one of the numbers. We ask you to delete as many numbers as possible so that the number composed of the remaining bits is not a prime number. (1 yes, 2 no). Output the remaining bits and this non prime number.
Idea:
This is a conclusion question.
There are 1,4,6,8,9, only one left.
The rest is that this number contains only 2,3,5,7. Then there are only two left, and the proof is given below.
Conclusion 1: if any number of these four numbers repeats, 11 can be divided, such as 22 and 33
Because the title has guaranteed that there will be no illegal situation, that is, there are no numbers such as 23, 37, 73, 2, 7, 3 and 5.
In other words, if there are two digits, it must not be a prime number.
Conclusion 2: only legal double digits will appear
Discuss the three digit situation:
- Needless to say, 523 and 253 can also be transformed into non prime numbers ending in 2 and 5.
- 2, 3, 7, 27 and 72 are not prime numbers. It doesn't matter where 3 is
- 2, 5, 7 or 2 and 7
- 3, 5, 7, 57 and 75 are not prime numbers. It doesn't matter where 3 is
Conclusion 3: all three digits containing only 2,3,5,7 can become legal two digits
Four digits can be changed into any three digits, and all three digits have been proved legal. More than five digits are directly repeated.
In conclusion, it is proved that
#include<bits/stdc++.h>
using namespace std;
string s;
int t, n;
int prime[105];
void pre()
{
for (int i = 1; i <= 100; i++) prime[i] = 1;
for (int i = 2; i <= 100; i++)
{
int flag = 1;
for (int j = 2; j <= sqrt(i); j++)
{
if (i % j == 0)
{
flag = 0;
break;
}
}
if (flag == 1)
{
prime[i] = 0;
}
}
}
void solve()
{
for (int i = 0; i < s.length(); i++)
{
if (s[i] == '1' || s[i] == '4' || s[i] == '6' || s[i] == '8' || s[i] == '9')
{
cout << 1 << endl;
cout <<s[i] << endl;
return;
}
}
cout << 2 << endl;
for (int i = 0; i < s.length()-1; i++)
{
for (int j = i + 1; j < s.length(); j++)
{
int temp = (s[i] - '0') * 10 + (s[j] - '0');
if (prime[temp] == 1)
{
cout << temp << endl;
return;
}
}
}
}
int main()
{
ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);
pre();
cin >> t;
while (t--)
{
cin >> n >> s;
solve();
}
return 0;
}
1562C Rings topic link: Click here to transfer
Meaning:
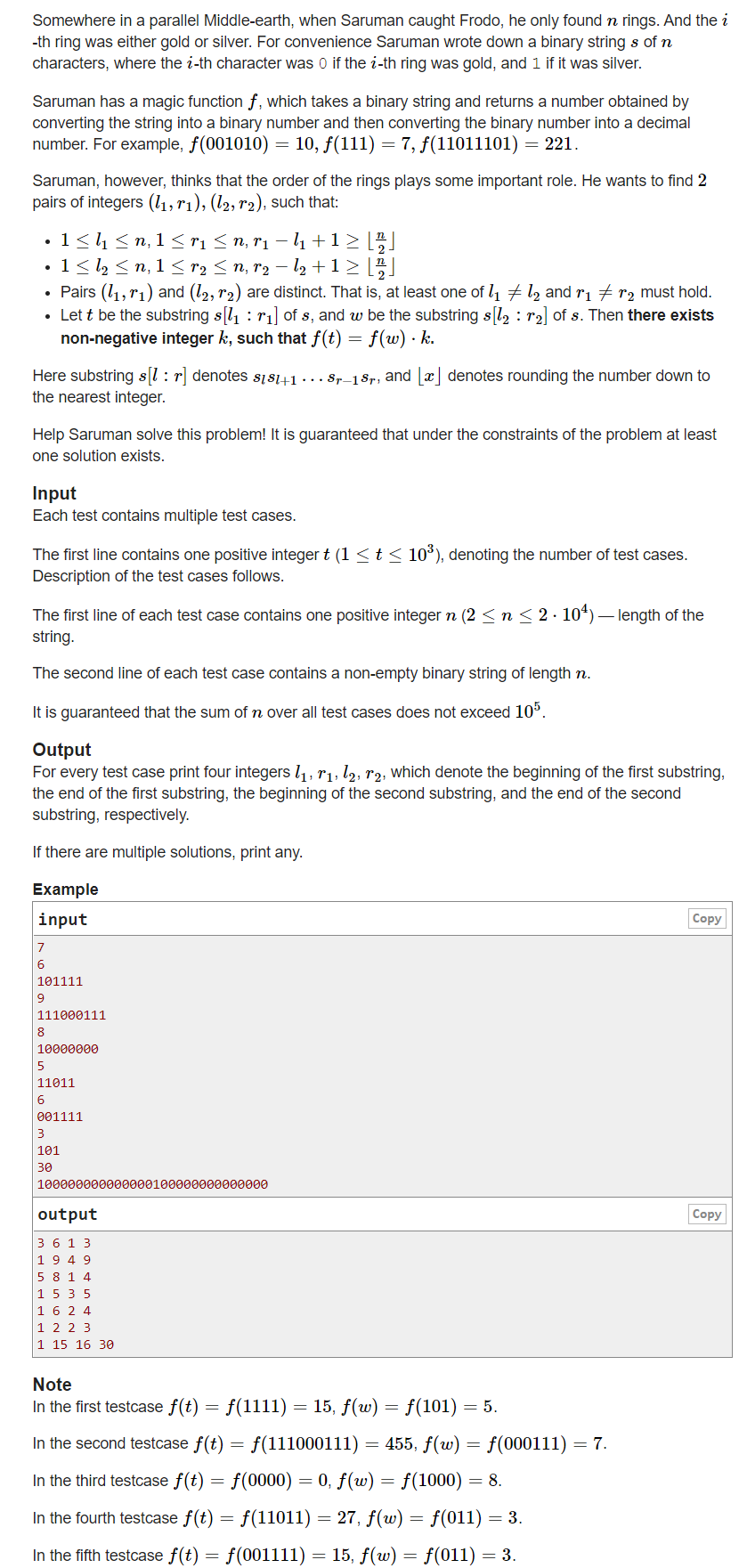
Give a 01 string, select two different substrings (the following values can be repeated), and their length should be greater than or equal to
n
2
\frac{n}{2}
2n. Convert the two substrings to decimal (leading zeros are removed), so that valuea=valueb
×
\times
×k,k
∈
\in
∈ nonnegative integer. Output the range of these two substrings
Idea:
- When the string is a full 1 string, output [ 1 , n − 1 ] \left[1,n-1\right] [1,n − 1] and [ 2 , n ] \left[2,n\right] [2,n], where k is 1
- When the first 0 of the string appears in the first half, the shape is 1110xxxxxxx. Set this position as pos and output
[
p
o
s
,
n
]
\left[pos,n\right]
[pos,n] and
[
p
o
s
+
1
,
n
]
\left[pos+1,n\right]
[pos+1,n], where k is 1
n-(pos+1)+1≥ n 2 \frac{n}{2} 2n
pos≤ n 2 \frac{n}{2} 2n
∵ \because ∵ in fact, the pos of the string starts from 0
∴ \therefore ∴pos< n 2 \frac{n}{2} 2n - When the first 0 of the string appears in the second half, the shape is 111111110xxxx. output [ 1 , p o s ] \left[1,pos\right] [1,pos] and [ 1 , p o s − 1 ] \left[1,pos-1\right] [1,pos − 1], k is 2
#include<bits/stdc++.h>
using namespace std;
string s;
int t, n;
void solve()
{
int index=-1;//The position of the first 0 in the string
for (int i = 0; i < s.length(); i++)
{
if (s[i] == '0')
{
index = i;
break;
}
}
if (index == -1)//All strings are 1
{
cout << 1 << " " << n - 1 << " " << 2 << " " << n << endl;
}
else if (index < n / 2)//011111 11111
{
cout << index + 1 << " " << n << " " << index + 2 <<" "<< n << endl;
}
else//111110 11111
{
cout << 1 << " " << index + 1 << " " << 1 << " " << index << endl;
}
}
int main()
{
ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);
cin >> t;
while (t--)
{
cin >> n >> s;
solve();
}
return 0;
}
1562D1 Two Hundred Twenty One (easy version) topic link: Click here to transfer
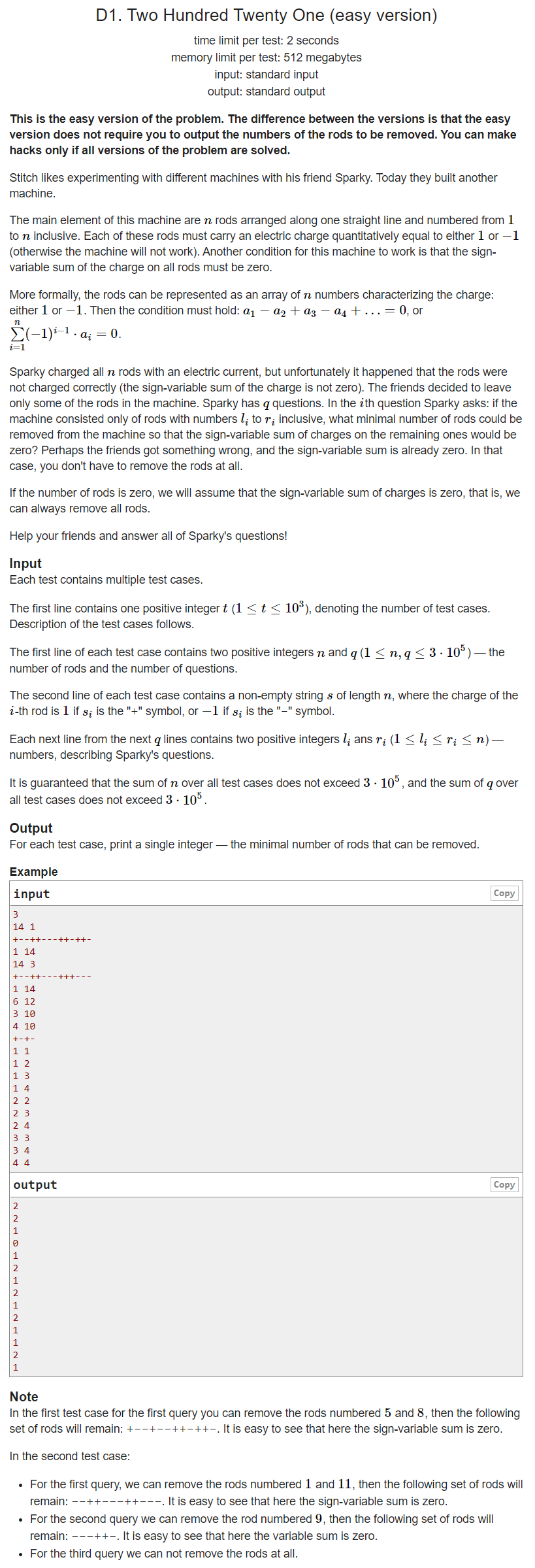
Meaning:
There is a string containing only '+' and '-' representing + 1 and - 1 respectively. selected
[
l
,
r
]
\left[l,r\right]
Substring within the range of [l,r], so that the value of this substring becomes
a
l
a_l
al,-
a
l
+
1
a_{l+1}
al+1,
a
l
+
2
a_{l+2}
al+2,......,
(
−
1
)
i
−
l
{(-1)}^{i-l}
(−1)i−l
×
\times
×
a
i
a_i
ai. Add up these values to get a number C. It is required to make C 0 by deleting some elements in the sequence (the following ones will be filled up after deletion). Output the number of deletions.
Idea:
Because the elements of these values are 1 and - 1, the final sequence length must be even. Delete at least one for odd numbers and at least two for even numbers (if it is not 0).
If a number is deleted, the following elements are added and the symbols are all reversed, which is equivalent to that a+x+b has become a-b=0. Obviously, this x exists because the element values are all 1 and a+b+x
≠
\neq
= 0. According to the above conclusion, if the value is directly 0, it will output 0, otherwise odd number will output 1 and even number will output 2 (delete a number arbitrarily before operation).
#include<bits/stdc++.h>
using namespace std;
#define MAXN 300005
int n, m, t;
string s;
int l, r;
int a[MAXN];
int sum[MAXN];//Odd and odd, even and even
int get(int l, int r)
{
int ans = 0;
if (l % 2 == 1 && r % 2 == 1) //+-+-+
{
int temp = max(0, l - 2);
ans = sum[r] - sum[temp];
ans -= sum[r - 1] - sum[l-1];
}
else if (l % 2 == 1 && r % 2 == 0) //+-+-
{
int temp = max(0, l - 2);
ans = sum[r - 1] - sum[temp];
ans -= sum[r] - sum[l-1];
}
else if (l % 2 == 0 && r % 2 == 1)//-+-+
{
ans = sum[r] - sum[l-1];
ans -= sum[r - 1] - sum[l - 2];
}
else//-+-+-
{
ans = sum[r - 1] - sum[l - 1];
ans -= sum[r] - sum[l - 2];
}
return ans;
}
int main()
{
ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);
cin >> t;
while (t--)
{
cin >> n >> m;
cin >> s;
for (int i = 0; i < s.length(); i++)
{
if (s[i] == '+') a[i + 1] = 1;
else a[i + 1] = -1;
}
sum[1] = a[1];
for (int i = 2; i <= n; i++)
{
sum[i] = sum[i - 2] + a[i];
}
while (m--)
{
cin >> l >> r;
int ans = 0;
//[l,pos-1]=x/2 pos [pos+1,r]=x/2
ans = get(l, r);
if (ans == 0) cout << 0 << endl;
else if ((r - l + 1) % 2 == 1) cout << 1 << endl;
else if ((r - l + 1) % 2 == 0) cout << 2 << endl;
}
}
return 0;
}
1562D2 Two Hundred Twenty One (hard version) topic link: Click here to transfer
Meaning:
The only difference from D1 is to output the location of the deleted element.
Push the formula and set the deletion position as pos,pos
∈
\in
∈
[
l
,
r
]
\left[l,r\right]
[l,r]:
sum[pos-1]-sum[l-1]=sum[r]-sum[pos]
sum[pos-1]+sum[pos]=sum[r]+sum[l-1]
Just find a pos that satisfies the above formula.
On how to prove that the prefix and the proof are still valid after the inversion of even bits, the official title is written, I can't understand it. food
As for the search process, the writing of O(n) will time out. The official explanation of the question has written two points, and the answer can't be understood. food
Give the code of the official solution directly.
#include <iostream>
using namespace std;
int a[1000000 + 5], p[1000000 + 5];
int get_sum(int l, int r) {
if (l > r) {
return 0;
}
return (l % 2 == 1) ? p[r] - p[l - 1] : p[l - 1] - p[r];
}
int check_elimination(int l, int r, int m) {
return ((m - l + 1) % 2 == 1)
? get_sum(l, m - 1) + get_sum(m + 1, r)
: get_sum(l, m - 1) - get_sum(m + 1, r);
}
int get_sign(int m) {
return m > 0 ? 1 : -1;
}
int calculate_odd_segment(int l, int r) {
if (l == r) {
return l;
}
int pos = 0;
int lb = l;
int rb = r;
while (lb < rb) {
int mb = (lb + rb) / 2;
int lq = check_elimination(l,r,lb);
int mq = check_elimination(l,r,mb);
int rq = check_elimination(l,r,rb);
if (lq == 0) {
pos = lb;
break;
}
if (mq == 0) {
pos = mb;
break;
}
if (rq == 0) {
pos = rb;
break;
}
if (get_sign(lq) == get_sign(mq)) {
lb = mb;
} else {
rb = mb;
}
}
return pos;
}
int main() {
ios_base::sync_with_stdio(false);
cin.tie(nullptr);
int t;
cin>>t;
while (t--) {
int n, q;
cin >> n >> q;
string ss;
cin >> ss;
for (int i = 1; i <= n; i++) {
a[i] = (ss[i - 1] == '+' ? 1 : -1);
}
p[0] = 0;
for (int i = 1; i <= n; i++) {
p[i] = p[i - 1] + (i % 2 == 1 ? a[i] : -a[i]);
}
for (int o = 0; o < q; o++) {
int l, r;
cin >> l >> r;
if (get_sum(l, r) == 0) {
cout << "0\n";
continue;
}
bool even = false;
if ((r - l + 1) % 2 == 0) {
even = true;
l++;
}
int pos = calculate_odd_segment(l, r);
if (even) {
cout << "2\n" << l - 1 << " "<< pos << '\n';
} else {
cout << "1\n" << pos << '\n';
}
}
}
}