Codeforces Round #648 Div. 2 Jun/07/2020 22:35UTC+8
Match links https://codeforces.com/contest/1365
Match record https://blog.csdn.net/cheng__yu_/article/details/105395197
B. Trouble Sort
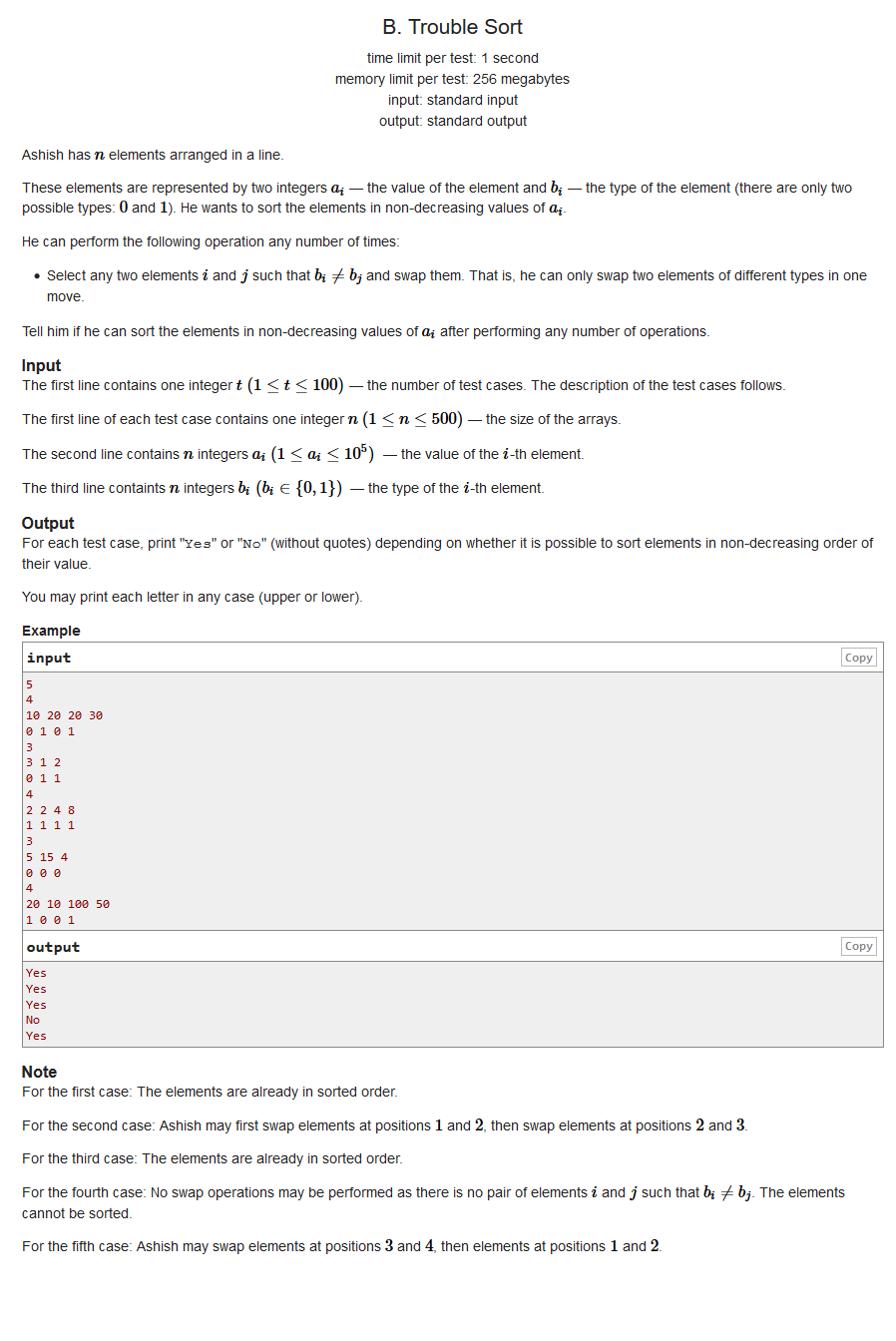
The array a of n elements is given. Each element has two types: 0 and 1. Different types can be exchanged. Ask if the given array can be replaced with a non descending array
Idea: as long as there are two different types of 0 and 1, they can be exchanged into any arrangement you want
#include <bits/stdc++.h> #define ll long long using namespace std; const int maxn=1e5+10,inf=2e9; int t,n; int a[maxn]; int main() { cin>>t; while(t--) { cin>>n; for(int i=1;i<=n;++i) cin>>a[i]; bool f[2]; f[0]=f[1]=0; for(int i=1;i<=n;++i) { int x;cin>>x; f[x]=true; } if(f[0]&&f[1]) { puts("Yes"); } else { bool ok=1; for(int i=2;i<=n;++i) { if(a[i-1]>a[i]) ok=0; } puts(ok?"Yes":"No"); } } return 0; }
C. Rotation Matching

Two arrays a and b with length n are given. You can cycle through the a array and ask how many pairs of a[i]=b[i].
Idea: the distance difference of the same number is equal
#include <bits/stdc++.h> #define ll long long using namespace std; const int maxn=2e5+10; int n; int a[maxn],b[maxn]; int pos1[maxn],pos2[maxn]; int main() { cin>>n; for(int i=1;i<=n;++i) { cin>>a[i]; pos1[a[i]]=i; } for(int i=1;i<=n;++i) { cin>>b[i]; pos2[b[i]]=i; } map<int,int> mp; for(int i=1;i<=n;++i) { int d=(pos1[i]-pos2[i]+n)%n; mp[d]++; } int ans=0; for(auto i : mp) { ans=max(ans,i.second); } printf("%d\n",ans); return 0; }
D. Solve The Maze
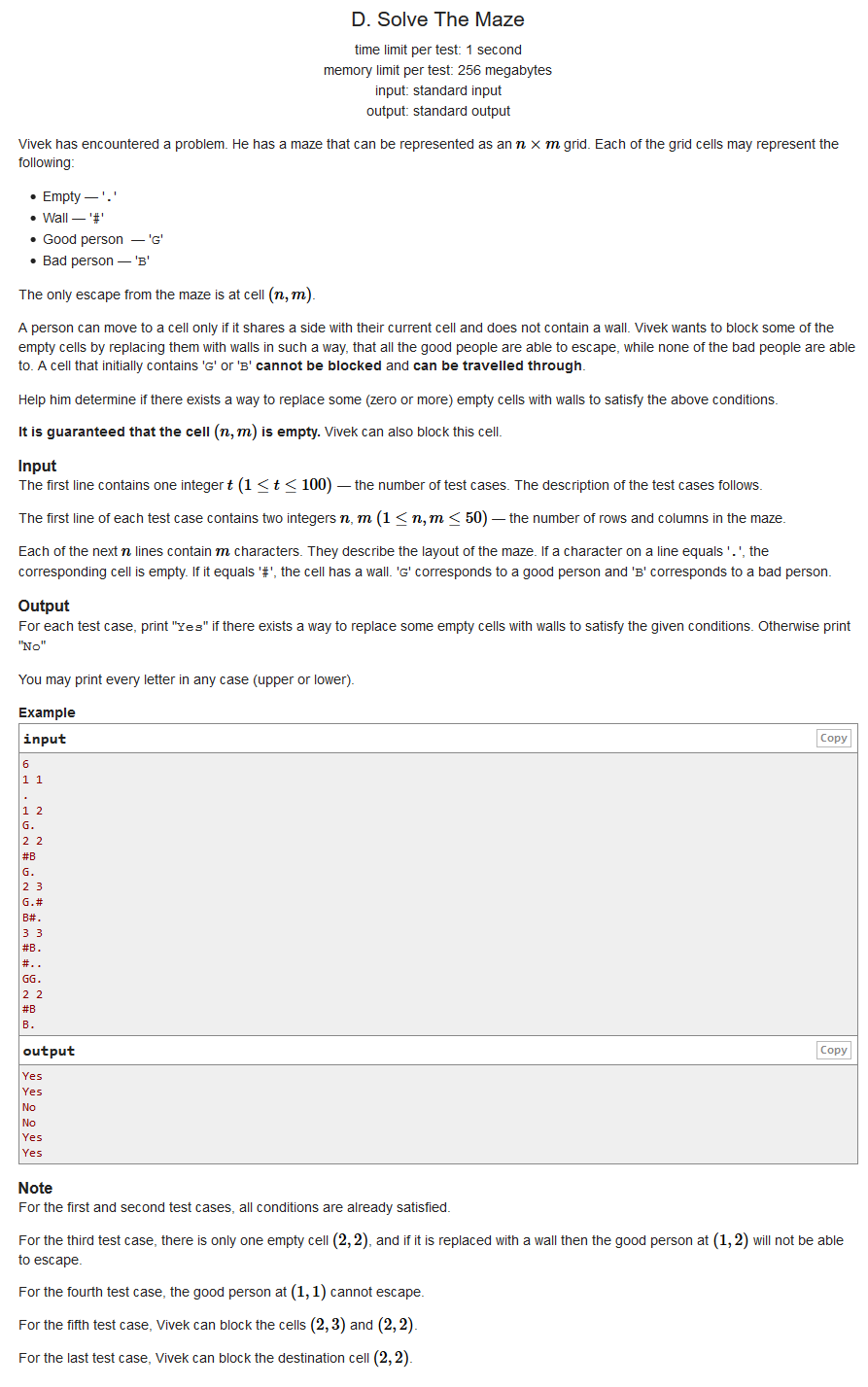
Given a graph of n × mn\times mn × m, there are good people (G) and bad people (B) on the graph, and the exit is (n, m). Now you can change some of the blank positions into walls. Ask if you can get all the good guys to the exit, and the bad guys can't escape
Idea: change the blank space around the bad guys into a wall, and then start dfs from (n, m) to see if you can go all the way to the good guys and not to the bad guys.
#include <bits/stdc++.h> #define ll long long using namespace std; const int maxn=2e5+10; int t,n,m; char mp[100][100]; int dx[]={0,0,-1,1}; int dy[]={1,-1,0,0}; int ok; int visit[60][60]; void dfs(int x,int y) { for(int i=0;i<=3;++i) { int nx=x+dx[i]; int ny=y+dy[i]; if(nx>=1&&nx<=n&&ny>=1&&ny<=m&&mp[nx][ny]!='#'&&!visit[nx][ny]) { if(mp[nx][ny]=='G') mp[nx][ny]='.'; if(mp[nx][ny]=='B') { ok=0; } visit[nx][ny]=1; dfs(nx,ny); } } } int main() { cin>>t; while(t--) { cin>>n>>m; for(int i=1;i<=n;++i) scanf("%s",mp[i]+1); bool exist=0; for(int i=1;i<=n;++i) { for(int j=1;j<=m;++j) { if(mp[i][j]=='B') { if(i>1&&mp[i-1][j]=='.') mp[i-1][j]='#'; if(i<n&&mp[i+1][j]=='.') mp[i+1][j]='#'; if(j>1&&mp[i][j-1]=='.') mp[i][j-1]='#'; if(j<m&&mp[i][j+1]=='.') mp[i][j+1]='#'; } if(mp[i][j]=='G') exist=1; } } if(mp[n][m]=='#'&&!exist) { puts("Yes"); continue; } ok=1; memset(visit,0,sizeof(visit)); dfs(n,m); if(ok) { bool finds=0; for(int i=1;i<=n;++i) for(int j=1;j<=m;++j) if(mp[i][j]=='G') finds=1; if(finds) ok=0; } puts(ok?"Yes":"No"); } return 0; }
E. Maximum Subsequence Value

The array a of n elements is given. Select the number of k. if the number of max(1,k-2) in the i-th position of the number of k is at least 1, then the contribution increases by 2I 2 ^ i2i to find the maximum contribution
#include <bits/stdc++.h> #define ll long long using namespace std; const int maxn=1e5+10,inf=2e9; int n; ll a[maxn]; int main() { cin>>n; for(int i=1;i<=n;++i) cin>>a[i]; ll ans=0; for(int i=1;i<=n;++i) for(int j=1;j<=n;++j) for(int k=1;k<=n;++k) ans=max(ans,a[i]|a[j]|a[k]); cout<<ans<<"\n"; return 0; }
F. Swaps Again (thinking)

Two arrays a and b with length n are given. You can operate on a, exchange the first k of a and the last K of a, and ask if you can finally change a array into b array
#include <bits/stdc++.h> #define ll long long using namespace std; const int maxn=500+10,inf=2e9; int t,n; int a[maxn],b[maxn]; int main() { cin>>t; while(t--) { cin>>n; for(int i=1;i<=n;++i) cin>>a[i]; for(int i=1;i<=n;++i) cin>>b[i]; bool ok=1; if(n&1&&a[n/2+1]!=b[n/2+1]) ok=0; map<pair<int,int>,int> mp; for(int i=1;i<=n/2;++i) { if(a[i]>a[n-i+1]) swap(a[i],a[n-i+1]); mp[{a[i],a[n-i+1]}]++; } for(int i=1;i<=n/2;++i) { if(b[i]>b[n-i+1]) swap(b[i],b[n-i+1]); pair<int,int> p={b[i],b[n-i+1]}; if(mp[p]<=0) ok=0; mp[p]--; } puts(ok?"Yes":"No"); } return 0; }